![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
関数 |
凌宮表記術: |
|



束縛されない変数を自由変数と呼び、束縛変数と区別する。
束縛変数を含まないし式を単に変数式と呼び、関数と区別する。
例えば、変数式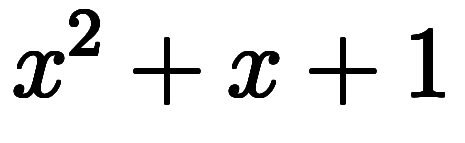 は関数
は関数 とは区別する
とは区別する
|
変数式の自由変数は、関数の束縛変数とは異なって差し替えが効かない。
変数

 であれば、一般的に
であれば、一般的に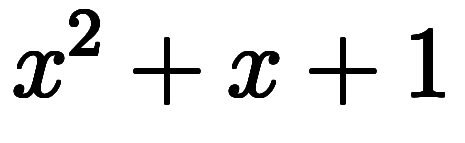 と
と は異なる。
は異なる。
|
一般に、多項式は変数式であり、関数ではない。
多項式では、不定元の勝手な書き換えは許されない。



関数の束縛変数に自由変数を代入すると、形式的に束縛変数を自由変数で置換した変数式が得られる。
|
|
特に同名の自由変数を代入した場合、形式的に束縛を解いた変数式が得られる。
|
|
ところが、同名と言っても、束縛表記の任意性のために実際は別名にも化けられる。
しかし、束縛変数を何に差し替えても、結果は解放で指定する自由変数によって唯一に決まる。
|
|
|
関数の束縛変数に自由変数を代入して関数から変数式を作る操作を解放と言う。



束縛変数の解放とは逆に、自由変数を束縛して変数式から関数を作る操作を束縛と言う。
変数式と関数の違いは、形式的に束縛の有無と見なせる。
束縛表記はその特性を生かした表記である。
一般に、

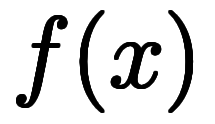

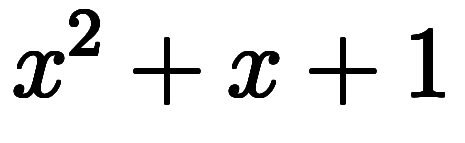 と書いた場合、
と書いた場合、
 を関数の独立変数、
を関数の独立変数、 を関数の従属変数と呼ぶが、
を関数の従属変数と呼ぶが、
定義式である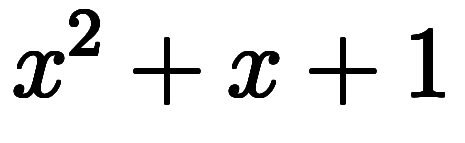 は従属変数に相当する変数である。
は従属変数に相当する変数である。
束縛表記における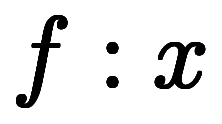

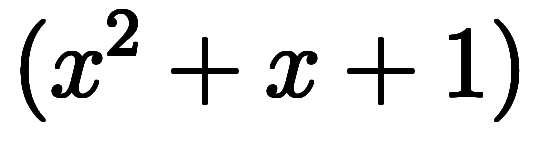
 は、
は、
従属変数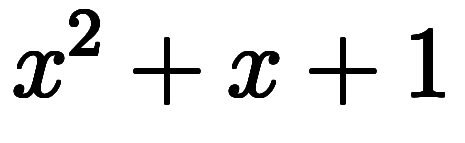 を独立変数
を独立変数 で束縛した式とも解釈できる。
で束縛した式とも解釈できる。
また、従属変数と独立変数を使って、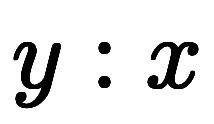 と表しても良いとする。
と表しても良いとする。
すなわち、
|



束縛表記では変数式と関数を厳密に区別するが、
束縛と解放により相互変換が可能になっている。



定数関数は代入した値に関係なく、定数を取る関数である。
例えば、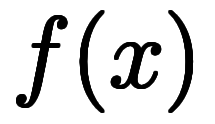

 は定数関数であり、関数値が代入した値に関係なく常に
は定数関数であり、関数値が代入した値に関係なく常に である。
である。
具体には、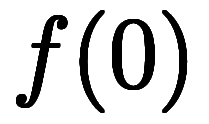
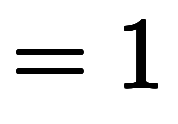 、
、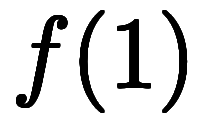
 、
、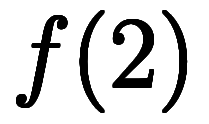
 ……。
……。
束縛表記では、定数 に対し、定数関数は
に対し、定数関数は と表記する*1。
と表記する*1。
ただし、この束縛は形式的なもので、実際に束縛される対象となる が変数式
が変数式 に含まれ無い。
に含まれ無い。
このため、定数関数に限り、束縛の有無は区別しない。
|






関数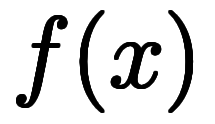 に定数を代入すると、束縛変数の無い定数になる。
に定数を代入すると、束縛変数の無い定数になる。
例えば、
|
|
これらは全て定数である。