![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
極限の分割 |
背景 |
|
| |
|
| |
| ||
|
| |
|
| |
|
| |
|
| |
| ||
|
 で示した変換の可否が問題となる。
で示した変換の可否が問題となる。



本題に入る前に、極限操作の分割を回避し、既に利用されている各項で上から抑える発想のみで解く方法を示す。
|
| |
|
| |
| ||
|
| |
|
| |
|
| |
| ||
|
最初の不等号では、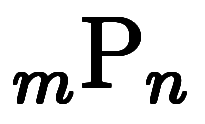

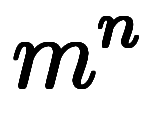 を利用している。例えば
を利用している。例えば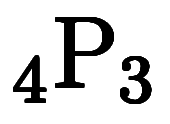

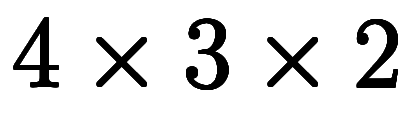



 である。
である。
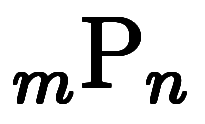




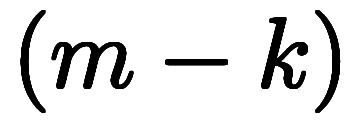 であり、各因数において
であり、各因数において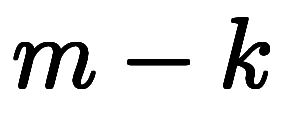

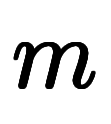 が言えるため、
が言えるため、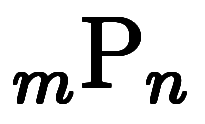


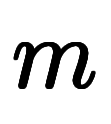

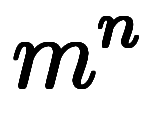 が成り立つ。
が成り立つ。
次の不等号では、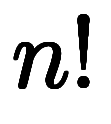

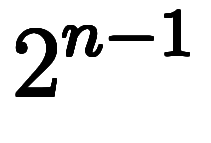 を利用している。例えば
を利用している。例えば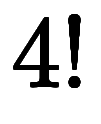





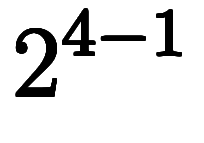 である。
である。
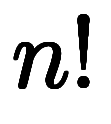

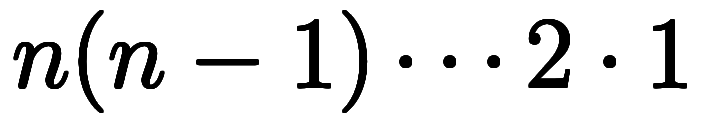


 であり、
であり、 を除き各因数において
を除き各因数において

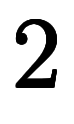 が言えるため、
が言えるため、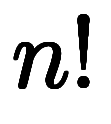



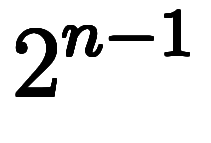 が成り立つ。
が成り立つ。






上下で押さえる発想だけで示せることを確認したところで、本題に入る。
示された手法の問題点は、極限を取る文字が形式的に複数回使われる式に対し、箇所毎に極限を取る操作の同値性と言える。
オリジナルの手法では、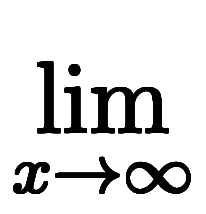


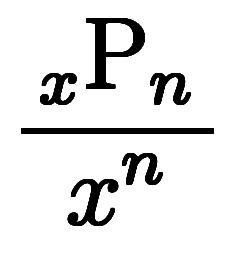 を
を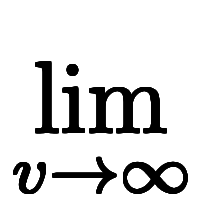
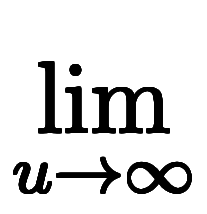


 に変換している。
に変換している。
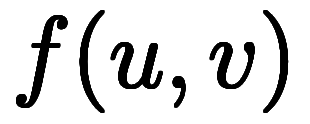

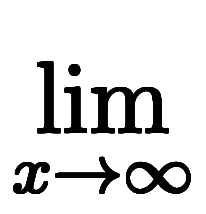

 と置けば、
と置けば、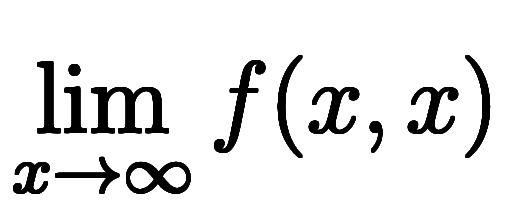
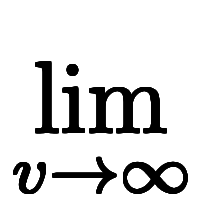
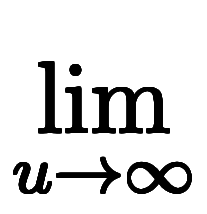
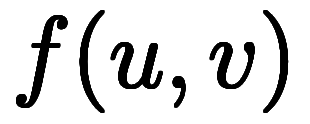 という問題になる。
という問題になる。
例えば、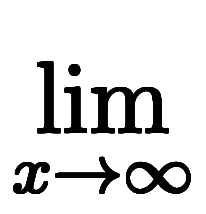
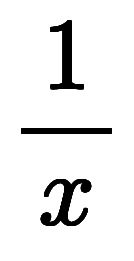

 について、
について、


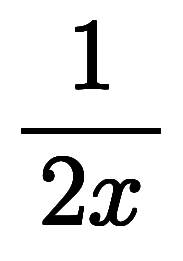

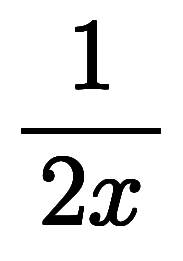 から
から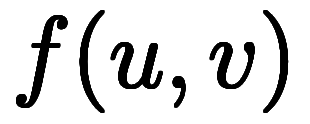

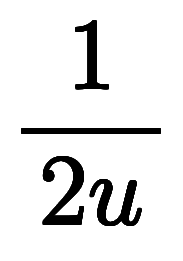

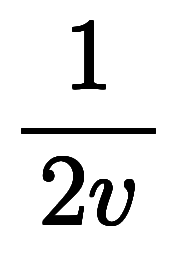
 を作っても、
を作っても、
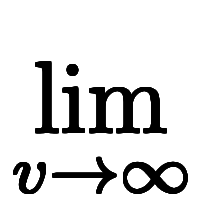
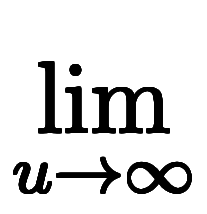
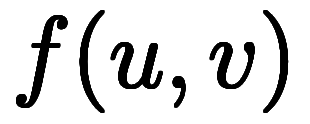

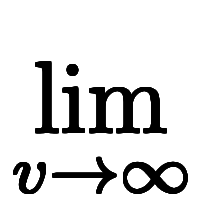
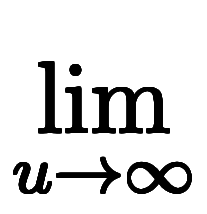

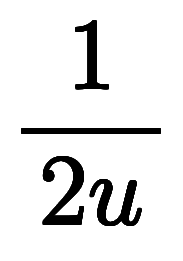

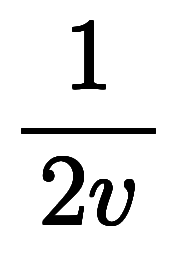


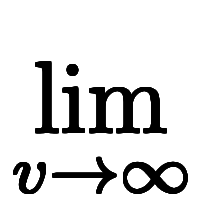



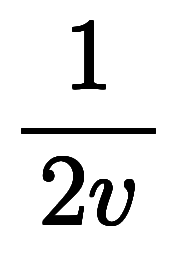


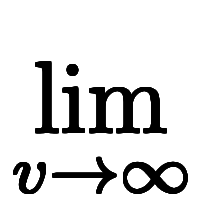
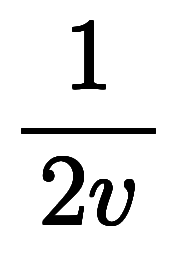

 と、
と、
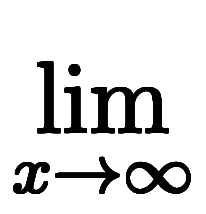
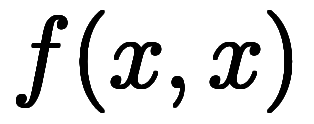

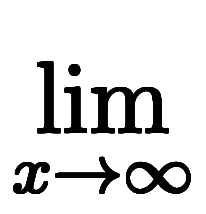


 に一致する。
に一致する。
しかし、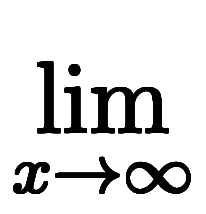


 について、
について、


 から
から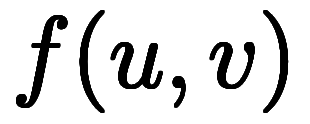

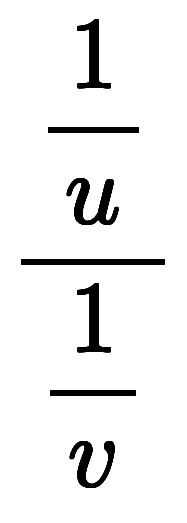 を作ったら、
を作ったら、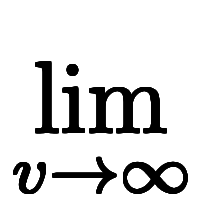
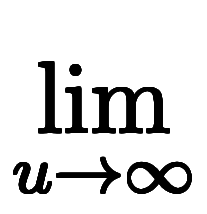
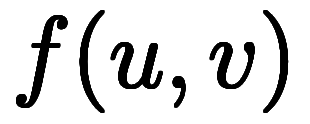

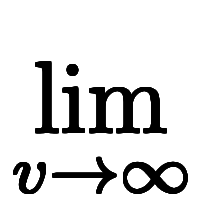
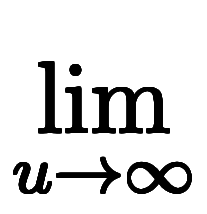


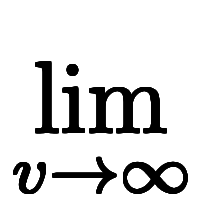
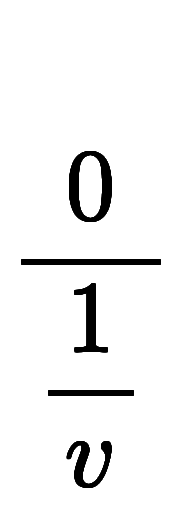

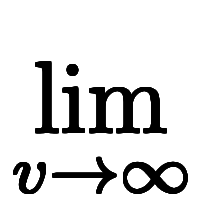


 と、
と、
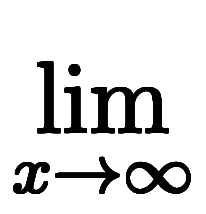
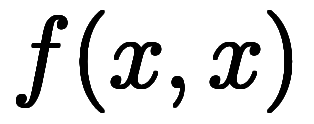

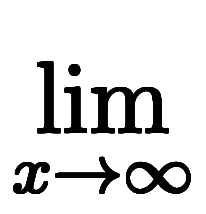


 とは異なる結果を出してしまう。
とは異なる結果を出してしまう。
よって、範囲を気軽に任意の2変数関数に広げては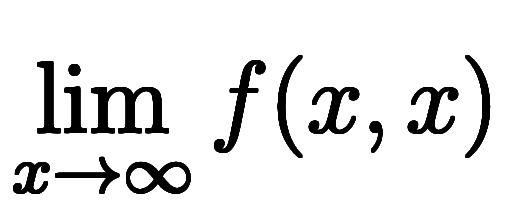

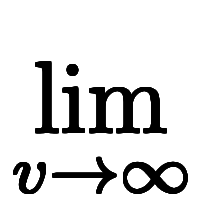
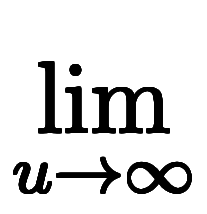
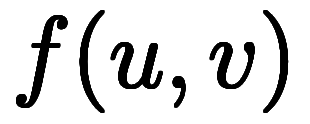 と成立しなくなる。
と成立しなくなる。
一般に、多変数関数では「接近経路に寄らずに一定の値を取る」ことが極限を定義できる条件になっている。
cf: http://webmath.las.osakafu-u.ac.jp/top/std/help/help0102011001.pdf
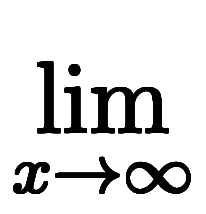
 は
は を
を の線上に沿って
の線上に沿って に近づけることに等しい。
に近づけることに等しい。
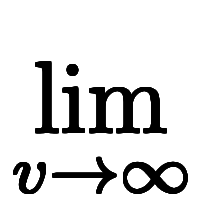
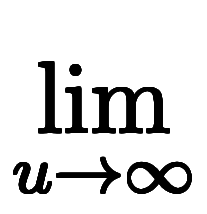
 は任意点
は任意点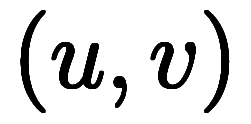 から出発し、
から出発し、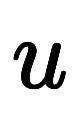 軸に平行に
軸に平行に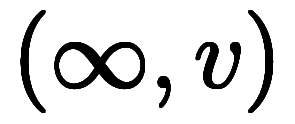 まで近づいてから、
まで近づいてから、
最終的に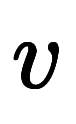 軸に平行に
軸に平行に に近づけることに等しい。
に近づけることに等しい。



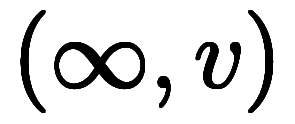 から
から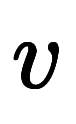 軸に平行に
軸に平行に に近づける経路はグラフにできないため、
に近づける経路はグラフにできないため、
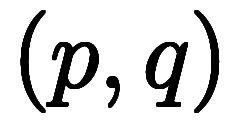

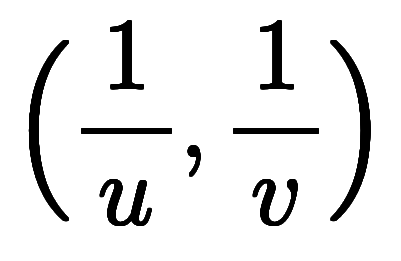 と定義して、
と定義して、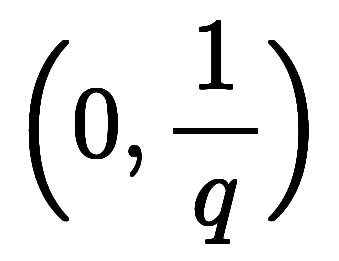 と
と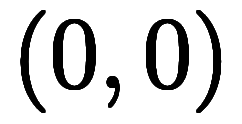 に変換して
に変換して の原点付近を図示してみる。
の原点付近を図示してみる。
対応する関数は、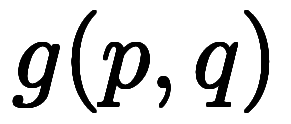

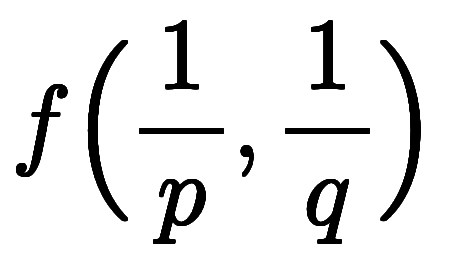

 であり、
であり、
考える極限と接近は、
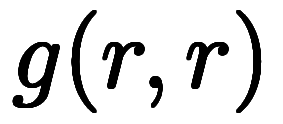







 という直線
という直線 に沿う接近と、
に沿う接近と、


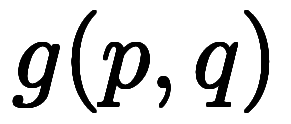











 という、
という、 かつ
かつ なる任意点
なる任意点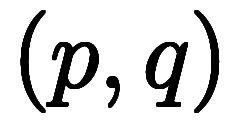 から出発し、
から出発し、
 軸に平行に
軸に平行に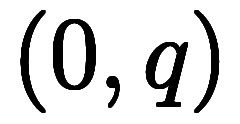 に近づいてから、最終的に
に近づいてから、最終的に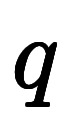 軸に平行に
軸に平行に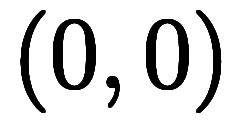 まで近づく接近になる。
まで近づく接近になる。
WolframAlphaで をプロットしてみると
をプロットしてみると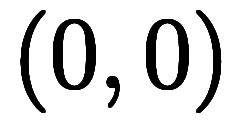 付近に捩じれた谷と山が見える。
付近に捩じれた谷と山が見える。
原点を除き、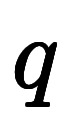

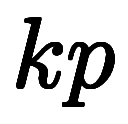 の線上は常に同じ値
の線上は常に同じ値 を取り、
を取り、

 付近では山と谷が隣り合わせになる。
付近では山と谷が隣り合わせになる。
原点付近は、近づいてくる方向によって、如何なる値も取れるわけである。
これは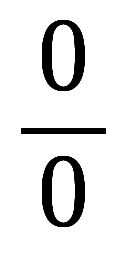 を定義できない理由でもある。
を定義できない理由でもある。



2変数関数に対して一般的に成立しないため、場合によってはこの成立条件を示す必要がある。
実際問題、少なくとも2階微分が可能なほどに滑らかな 級の関数であれば、任意方向に滑らかで連続的ということで要件を満たす。
級の関数であれば、任意方向に滑らかで連続的ということで要件を満たす。

細かい証明を示すには、
2変数関数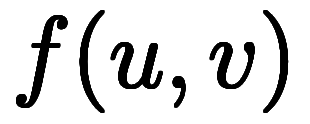 の分割極限
の分割極限

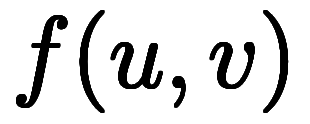



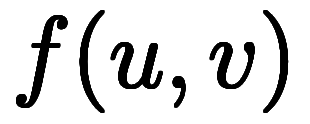 に対し、
に対し、
1変数に束縛した関数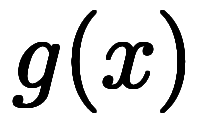

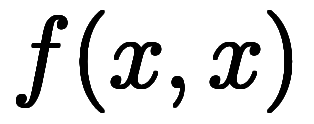 の極限
の極限
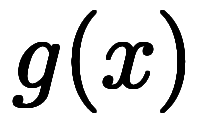 が存在するとして、
が存在するとして、
両者が一致するか。
|
もし

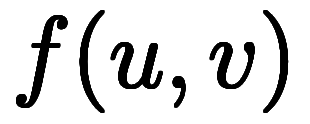



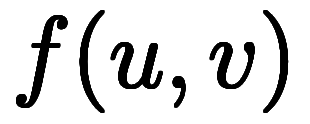 であれば、
であれば、
極限を取る順番を入れ替えることで異なる値を取る両者に共通の値を対応できないため、不成立は自明である。
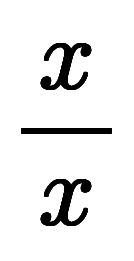
この可換性は、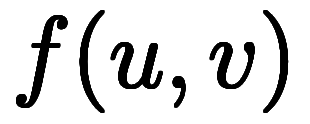 の極限
の極限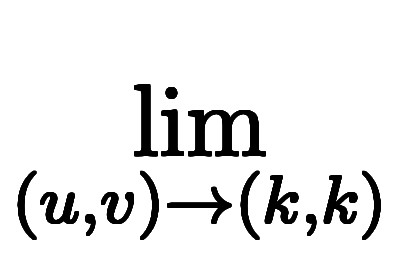
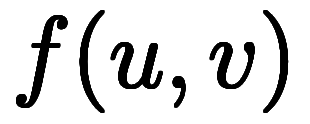 の存在条件ともされ、f(u,v)が微分可能なら
の存在条件ともされ、f(u,v)が微分可能なら
$$ \lim_{(u,v)\to(k,k)} $ \lim_{u\to k} $ f(u,v) $
そのため、



この手法が優れているのは、直観的な正項級数にあるとも。
例えば、 を証明する類の問題では、適当な項まで計算して打ち切れば下端を出せて、適当な等比数列の級数で上から押さえれば上端を出せる。
を証明する類の問題では、適当な項まで計算して打ち切れば下端を出せて、適当な等比数列の級数で上から押さえれば上端を出せる。
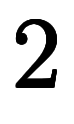 に
に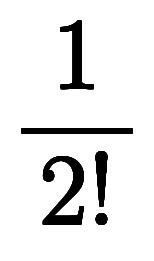

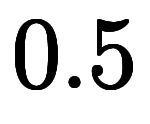 を加えても
を加えても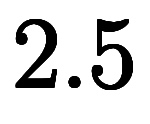 と欲しい下限
と欲しい下限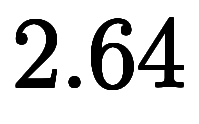 より大きいが、
より大きいが、
更に

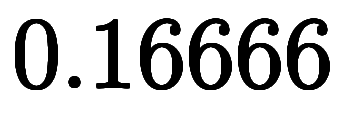 を加えて
を加えて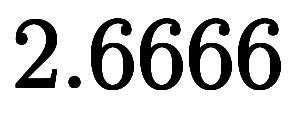 にすれば
にすれば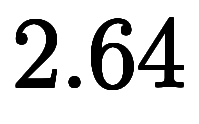 より十分に大きい下限を得られる*1。
より十分に大きい下限を得られる*1。
残差は

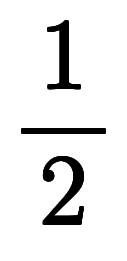

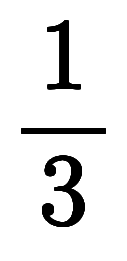

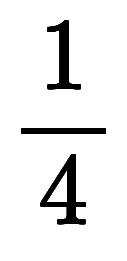 からの級数で、
からの級数で、

 さえ括りだせば、他の因数を全て
さえ括りだせば、他の因数を全て と見なした緩い上端を出せる。
と見なした緩い上端を出せる。


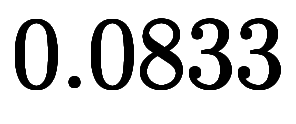 のため、
のため、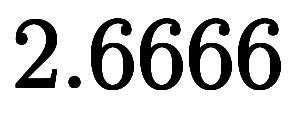 に加えれば
に加えれば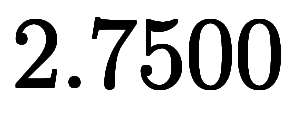 という
という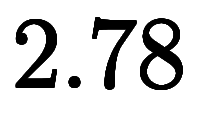 に対して十分に小さい上端を得られる。
に対して十分に小さい上端を得られる。