Dx45y=0 < 定数係数２階線形常微分方程式

$\ddd{^2y}{x^2}$ $\ddd{y}{x}$

固有値が虚数２つ、同次形

$\ddd{^2y}{x^2}$ $\ddd{y}{x}$
⇔ $\bigg($ $\ddd{^2}{x^2}$ $\ddd{}{x}$ $\bigg)$	式1：線形常微分演算子化
⇔ $\bigg($ $\ddd{}{x}$ $\:i$ $\bigg)$ $\bigg($ $\ddd{}{x}$ $\:i$ $\bigg)$	式2：線形常微分演算子の因数分解（ $\:i$ は虚数単位）
⇔ $\bigg($ $\ddd{}{x}$ $\:i$ $\bigg)^{\!\!-1\!\!} \bigg($ $\ddd{}{x}$ $\:i$ $\bigg)^{\!\!-1}$	式3：逆演算子表記
⇔ $e^{-(2+\:i)x} \!\!\!\int\!\! e^{(2+\:i)x}$ $\cdot$ $e^{-(2-\:i)x} \!\!\!\int\!\! e^{(2-\:i)x}$ $\cdot$	式4：逆演算子を積分に置換*1
⇔ $e^{-(2+\:i)x}$ $\int$ $e^{2\:ix}$ $\int$	式5：２階の積分式

以下からは具体的な積分計算が始まる。

$e^{-(2+\:i)x}$ $\int$ $e^{2\:ix}$ $\int$
$e^{-(2+\:i)x}$ $\int$ $e^{2\:ix}$ $\bigg[$ $\bigg]$
$e^{-(2+\:i)x}$ $\int$ $e^{2\:ix}$	式6：不定積分、は積分定数
$e^{-(2+\:i)x}$ $\bigg[$ $\ffd{C_1}{2\:i}e^{2\:ix}$ $\bigg]$
$\ffd{C_1}{2\:i}$ $e^{-(2-\:i)x}$ $e^{-(2+\:i)x}$	式7：不定積分、は積分定数

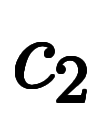
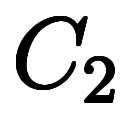ここで、 $$ c_1 $$ $$ = $$ $\ffd{C_1}{2\:i}$ 、 $$ c_2 $$ $$ = $$ と置いて式整理すると積和形の解が得られる。

$$ y $$ $$ = $$ $$ c_1 $$ $e^{-(2-\:i)x}$ $$ + $$ $$ c_2 $$ $e^{-(2+\:i)x}$

式8*：複素数版、積和形の一般解

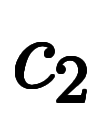しかし、この解は例え定数 $$ c_1 $$ と $$ c_2 $$ に実数を選んでも $$ y $$ が虚数値となりうる*2。
一方で、 $$ y $$ を実数値に限定する場合が多く、そのために以下の式変形が求められる。

$e^{-(2-\:i)x}$ $e^{-(2+\:i)x}$
$e^{-2x}$ $e^{\:ix}$ $e^{-2x}$ $e^{-\:ix}$
$e^{-2x}$ $\cos$ $\:i$ $\sin$ $e^{-2x}$ $\cos$ $\:i$ $\sin$	オイラーの公式 $e^{\:i\theta}$ $\cos$ $\theta$ $\;i$ $\sin$ $\theta$ を適用
$e^{-2x}$ $\cos$ $\:i$ $e^{-2x}$ $\sin$

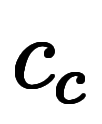
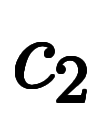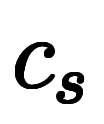
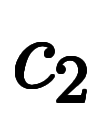
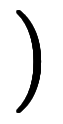
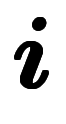ここで、 $$ c_c $$ $$ = $$ $$ c_1 $$ $$ + $$ $$ c_2 $$ 、 $$ c_s $$ $$ = $$ $$ ( $$ $$ - $$ $$ ) $$ $\:i$ と置いて式整理する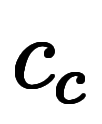と、
と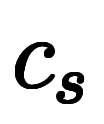を実数から取れば、 $$ y $$ も必ず実数になる積和形の解が得られる*3。
また、指数部が共通しているため、指数部を纏めた和積形が好まれる。