![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
部分分数分解と剰余定理 |
概要 |
||||||||||||||||||||||||||
| ラプラス変換表 | ||||||
|---|---|---|---|---|---|---|
原関数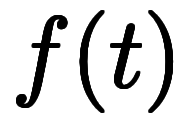 |  |  | 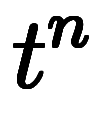 |  | 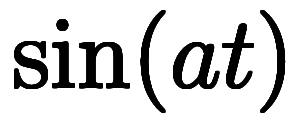 | 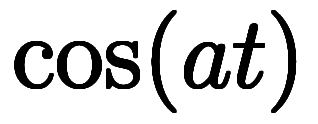 |
像関数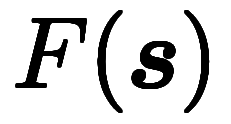 | 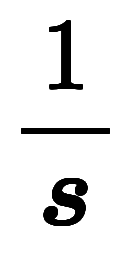 |  | 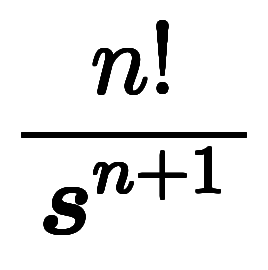 | 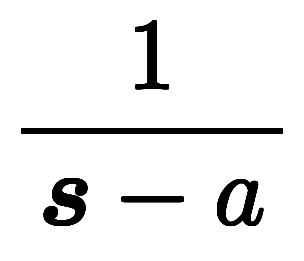 | 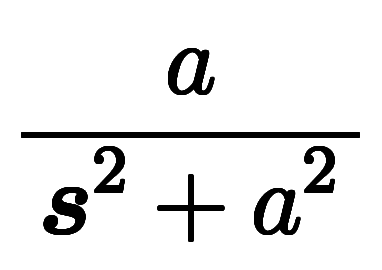 | 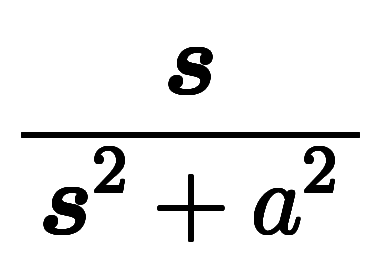 |
ここで、良く使う関数のラプラス変換結果は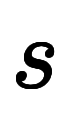 の有理式*3になっているのが分かる。
の有理式*3になっているのが分かる。
このため、ラプラス変換で線形微分方程式を解く際には、複雑な有理式を表内の有理式に分解する計算が大量発生する。
例えば、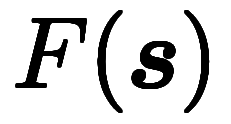



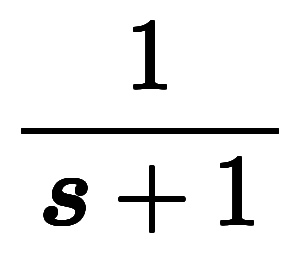

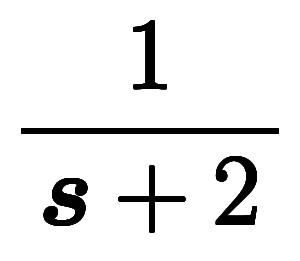 。
。
表内の分数の線形結合にさえ分解できれば、直ちに微分方程式の解が分かる。
例の場合は、

 より、
より、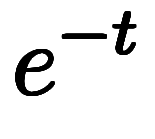

 、
、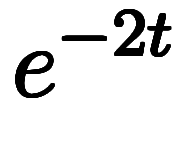

 が分かり、
が分かり、
方程式の解はラプラス変換が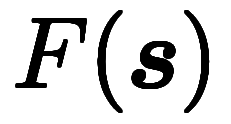 になる関数
になる関数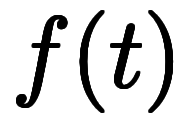

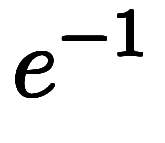

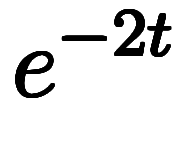 となる。
となる。
分母の因数分解で

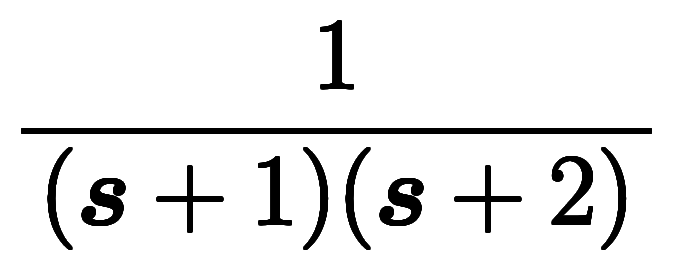 までは良いが、
までは良いが、
その先は恒等式



 を解くことになる。
を解くことになる。
この分母が高次多項式の有理式を、分母が低次多項式の有理式の線形和に分解する式変形を部分分数分解と言う。
部分分数分解は分母を払ってから展開して係数比較しても地道に解けるが、次のテクニックが良く知られている。
|
|



一般に、多項式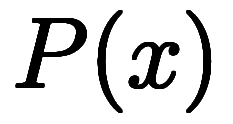 を1次式
を1次式 で割った商を
で割った商を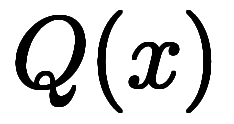 、余りを
、余りを と置くと、
と置くと、
|
と表せて、
|
が成り立つ。
これが高校で学ぶ剰余定理である。
そこで、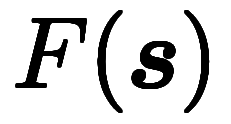



 を眺めてみると、
を眺めてみると、
 の分母を払って、
の分母を払って、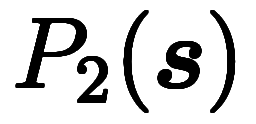

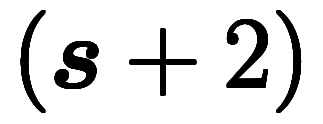
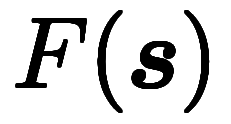




 と置くと、剰余定理とそっくりな式を作り出せる。
と置くと、剰余定理とそっくりな式を作り出せる。
そのため、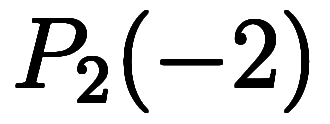






 が導ける*4。
が導ける*4。
同様に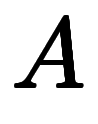 の分母を払えば、
の分母を払えば、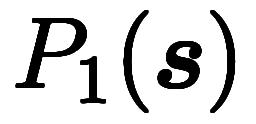

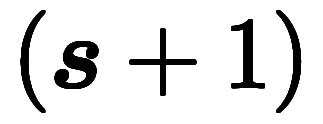
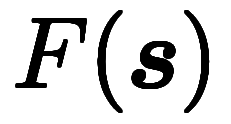

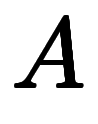


 と置くと、
と置くと、
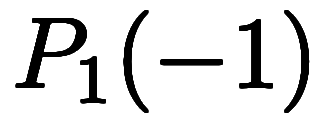

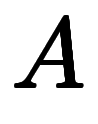

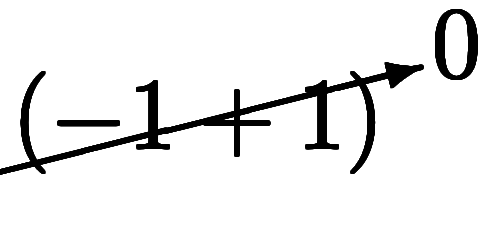
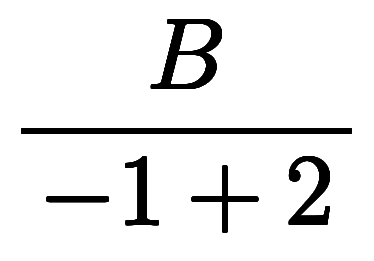

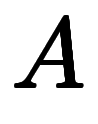 が得られる。
が得られる。
そこで、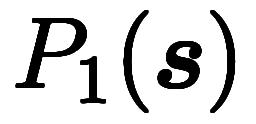 や
や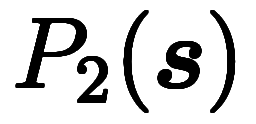 の計算に使う
の計算に使う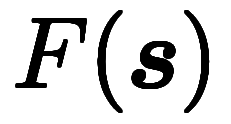 に
に を使えば、
を使えば、
前節で紹介した部分分数分解のテクニックとなる。