![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
指数対数の合成関数の無限級数展開 のバックアップ(No.5) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
指数対数の合成関数の無限級数展開 のバックアップ(No.5) |
設問 |
|
|
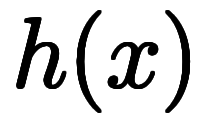

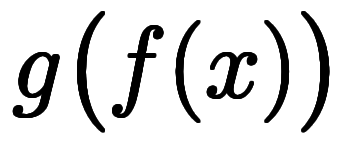 とすると、指数計算により
とすると、指数計算により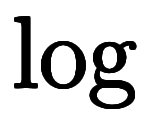 と
と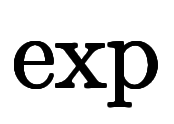 が打消し、簡単な式になる:
が打消し、簡単な式になる:
|
一方で、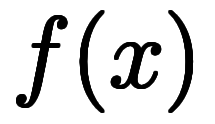 と
と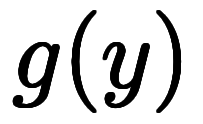 を級数展開しても
を級数展開しても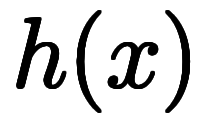 の級数の形で求まるはず:
の級数の形で求まるはず:
|
|
よって: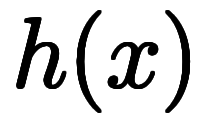

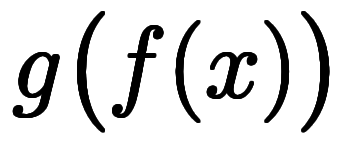


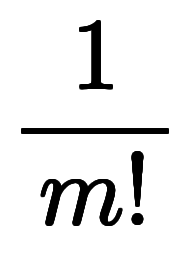
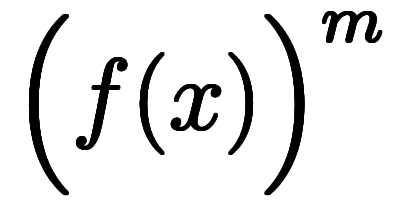



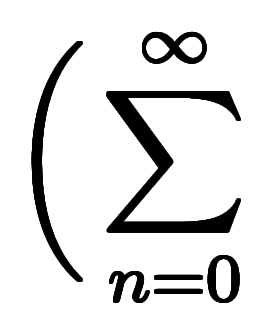
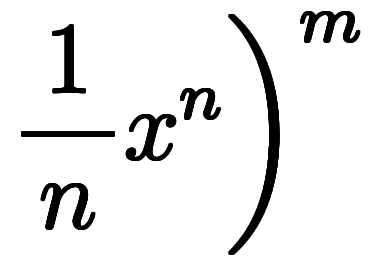
一方で、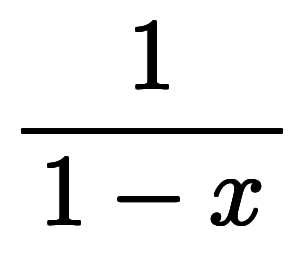


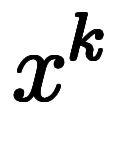 *2のため、
*2のため、

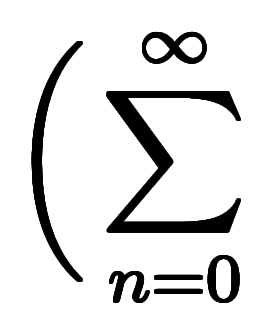
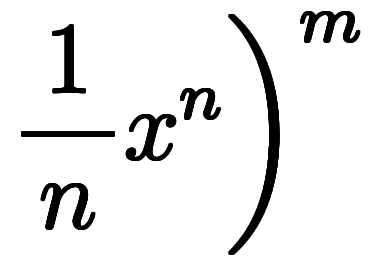


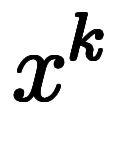 が成り立つ。
が成り立つ。
そこで係数比較すると、任意の

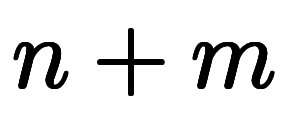 について
について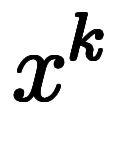 の係数は1でなければならない結論に至る。
の係数は1でなければならない結論に至る。
が、真面目に展開しても無限級数の入子であるため、簡単には導けない。





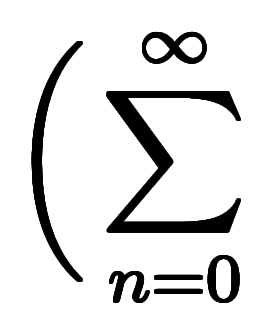
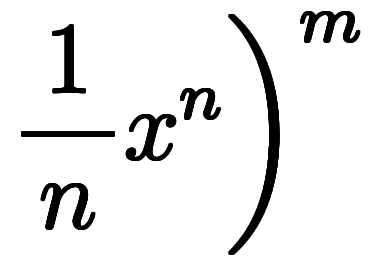 について、
について、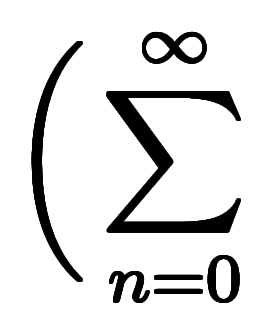
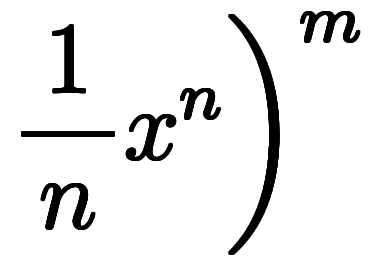 の部分は
の部分は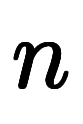 次多項式の
次多項式の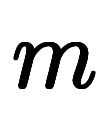 乗展開を意味する。
乗展開を意味する。
このため、直接多項式展開の記述
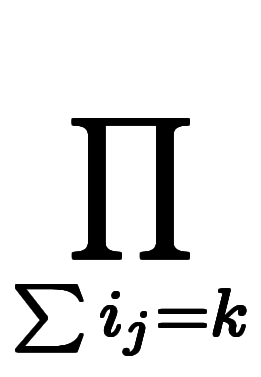
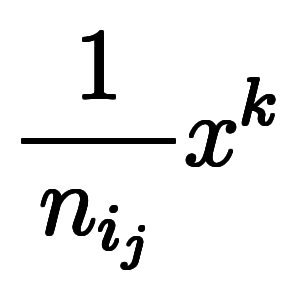 に置き換えできる。
に置き換えできる。
したがって、

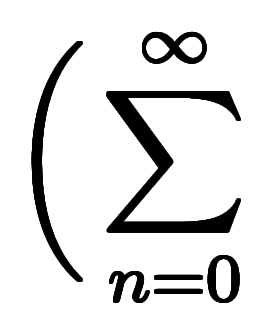
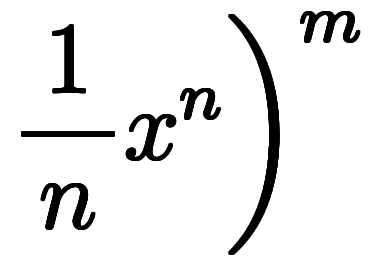





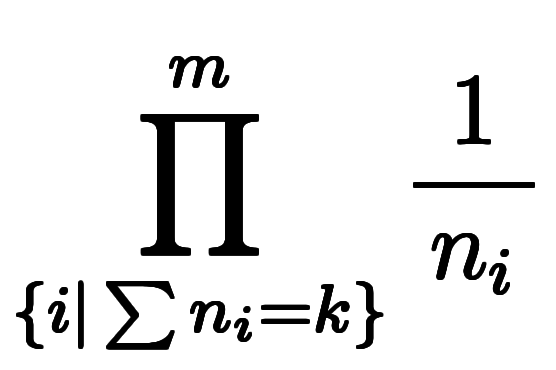

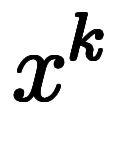






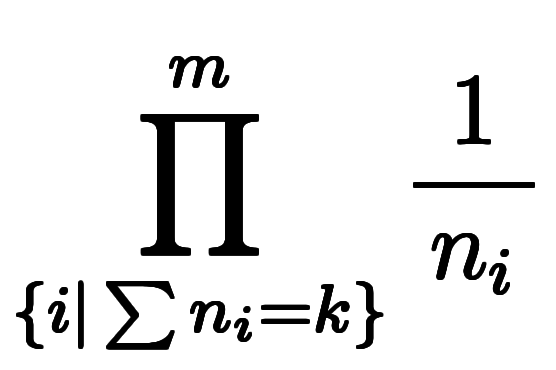

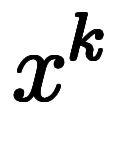
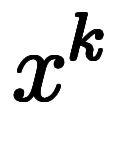 の係数を抜き出すと、任意の
の係数を抜き出すと、任意の について以下の式が成り立つ。
について以下の式が成り立つ。
|
ここで、総乗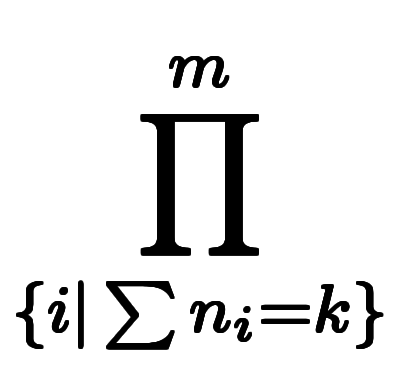 の条件式は、自然数範囲で
の条件式は、自然数範囲で について多項の加数分解を行い、結果の加数の総乗を取る意味である。
について多項の加数分解を行い、結果の加数の総乗を取る意味である。
また、上限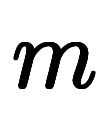 は、加数分解結果より
は、加数分解結果より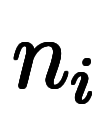 項数が決まり、
項数が決まり、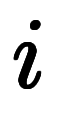 の上限である
の上限である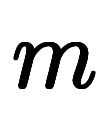 が逆に制限されることを意味する。
が逆に制限されることを意味する。
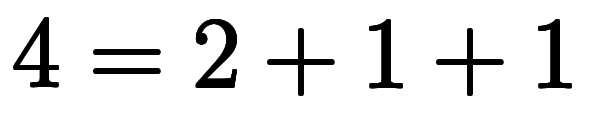
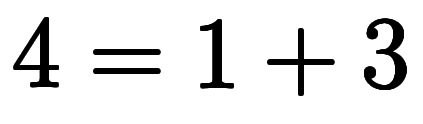
例えば、具体的に の場合、
の場合、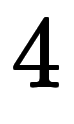 を以下のように加数分解を行い、
を以下のように加数分解を行い、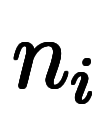 と
と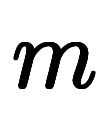 を決まる:
を決まる:
| 加数分解 | ![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png) | 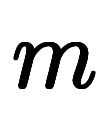 |
|---|---|---|
 | ![[4] $$ [4] $$](./eq/eq-ni-c29b8876a475c3670a3c12b9f86f83cd.png) |  |
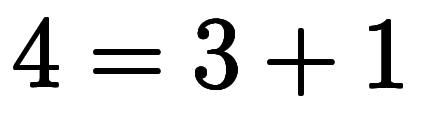 | ![[3, 1] $$ [3, 1] $$](./eq/eq-ni-bc85cb1ca723579e3620fd58f0f81c6e.png) |  |
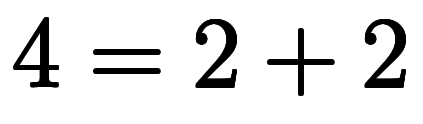 | ![[2, 2] $$ [2, 2] $$](./eq/eq-ni-cb0d829508e9fe594a58bea7221afebe.png) |  |
 | ![[1, 1, 1] $$ [1, 1, 1] $$](./eq/eq-ni-6c8b1ef6d34ffe22ff722f5e384139ee.png) | 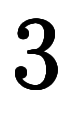 |
 | ![[1, 3] $$ [1, 3] $$](./eq/eq-ni-c911ba0bf98ba221800ba849d25a3521.png) | 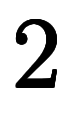 |
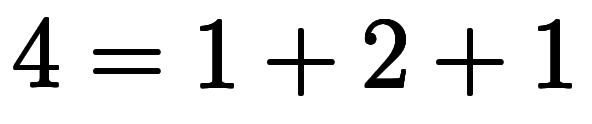 | ![[1, 2, 1] $$ [1, 2, 1] $$](./eq/eq-ni-8c5f162f7cb021763d4f79db6659fbb4.png) | 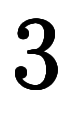 |
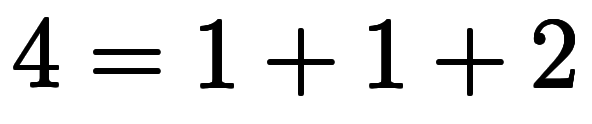 | ![[1, 1, 2] $$ [1, 1, 2] $$](./eq/eq-ni-a5219a4f32bb9b06d4631505d37c8383.png) | 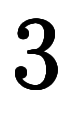 |
 | ![[1, 1, 1, 1] $$ [1, 1, 1, 1] $$](./eq/eq-ni-bdee9a930a273f9def272529f48c9ba9.png) | 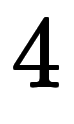 |
ところで、この総乗は厄介すぎるので、 についての漸化式を見いだして数学的帰納法を使う方法を検討してみる。
についての漸化式を見いだして数学的帰納法を使う方法を検討してみる。



これまでの調べで、項の数が の加数分解の可能性と分かった。
の加数分解の可能性と分かった。
このため、次の発想で項の和と漸化式に適する順番が決まる。
例えば の場合、
の場合、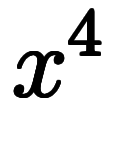 は5つの
は5つの の積を意味する。
の積を意味する。
|
ここで、 の加数分解は、
の加数分解は、 のグルーピングと解釈できる。
のグルーピングと解釈できる。
図形的に見ると、上式の「・」に任意に仕切り「|」を入れる操作と等価である。
このため、 個の
個の の間という
の間という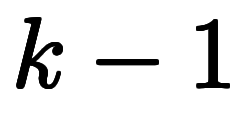 個の場所について、「|」を入れる・入れないの2通りの選択ができ、
個の場所について、「|」を入れる・入れないの2通りの選択ができ、
全部で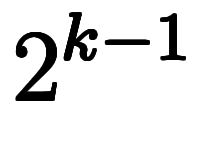 個の項が存在することになる。
個の項が存在することになる。
また、次の表のように考えると、 の段から
の段から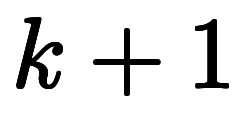 の段を機械的に作り出すことが可能になる。
の段を機械的に作り出すことが可能になる。