![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
フーリエ変換 のバックアップ(No.2) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
フーリエ変換 のバックアップ(No.2) |
フーリエ変換と逆基底と基底積 |
正変換: |
|
具体的に、時間 と周波数
と周波数 が互いに逆基底の関係にある基底と見なせば、
が互いに逆基底の関係にある基底と見なせば、
関数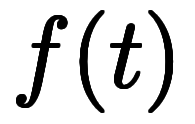 と
と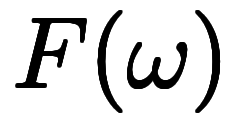 をそれぞれ
をそれぞれ と
と を基底とするベクトル*4で、
を基底とするベクトル*4で、
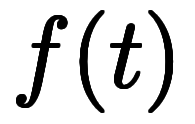 と
と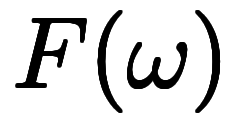 は同一現象を異なる基底に基づいて記述した一対の関数に見える。
は同一現象を異なる基底に基づいて記述した一対の関数に見える。
一方で、空間は波数と双対関係になる。
このため、フーリエ変換の空間版は次のように定義される*5。
正変換: |
|
3次元空間を含む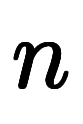 次元空間においてフーリエ変換を定義できる。
次元空間においてフーリエ変換を定義できる。
正変換: |
|
 が多用されるが、
が多用されるが、 倍違いの周波数
倍違いの周波数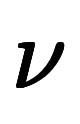 も用いられる。
も用いられる。 が多用される上に単に波数と呼ぶ場合が多いが、
が多用される上に単に波数と呼ぶ場合が多いが、 倍違いの波数
倍違いの波数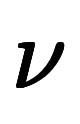 も用いられるため、定義に要注意。
も用いられるため、定義に要注意。 が多用される上に単に波数と呼ぶ場合が多いが、
が多用される上に単に波数と呼ぶ場合が多いが、 倍違いの波数
倍違いの波数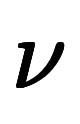 も用いられるため、定義に要注意。
も用いられるため、定義に要注意。