![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
フーリエ変換 のバックアップ(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
フーリエ変換 のバックアップ(No.3) |
フーリエ変換と逆基底と基底積 |
式1a 正変換: |
|
具体的に、時間 と周波数
と周波数 が互いに逆基底の関係にある基底と見なせば、
が互いに逆基底の関係にある基底と見なせば、
関数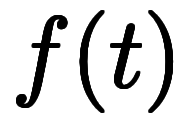 と
と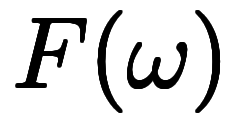 をそれぞれ
をそれぞれ と
と を基底とするベクトル*4で、
を基底とするベクトル*4で、
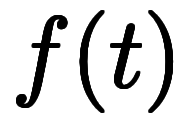 と
と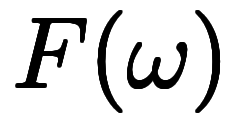 は同一現象を異なる基底に基づいて記述した一対の関数に見える。
は同一現象を異なる基底に基づいて記述した一対の関数に見える。
一方で、空間は波数と双対関係になる。
このため、フーリエ変換の空間版は次のように定義される*5。
式2a 正変換: |
|
3次元空間を含む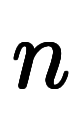 次元空間においてフーリエ変換を定義できる*7。
次元空間においてフーリエ変換を定義できる*7。
式3a 正変換: |
|
 が多用されるが、
が多用されるが、 倍違いの周波数
倍違いの周波数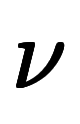 も用いられる。
も用いられる。 が多用される上に単に波数と呼ぶ場合が多いが、
が多用される上に単に波数と呼ぶ場合が多いが、 倍違いの波数
倍違いの波数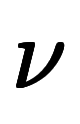 も用いられるため、定義に要注意。
も用いられるため、定義に要注意。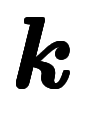 自体に
自体に 倍違いの2通りの定義があり、定義に要注意。
倍違いの2通りの定義があり、定義に要注意。


 や
や と
と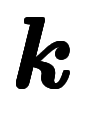 の通釈にあるように、
の通釈にあるように、
フーリエ変換において逆変換に現れる係数 の扱いが混乱の元となる。
の扱いが混乱の元となる。
例えば、式1a・式1bの時間に関するフーリエ変換では、角周波数 を
を で割った周波数
で割った周波数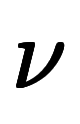 を使えば式4a・式4bのようになる。
を使えば式4a・式4bのようになる。
式4a 正変換: |
|



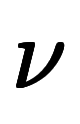 がために、逆変換に付く係数が隠れる代わりに、
がために、逆変換に付く係数が隠れる代わりに、
積分変換のカーネル関数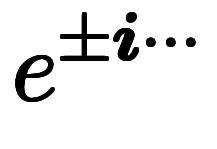 に
に が現れる。
が現れる。
このため、書く側は都度定義をし、読む側は都度確認する必要がある。



式3aと式3bの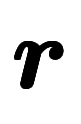 と
と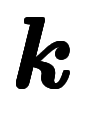 による積分は、体積分である。
による積分は、体積分である。
特に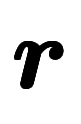 は位置ベクトルそのものであるため、線積分と非常に紛らわしい。
は位置ベクトルそのものであるため、線積分と非常に紛らわしい。
実際、文脈と積分領域での区別になる。
対して、一般的な3次元の体積分で良く用いられる記法では、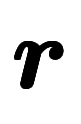 と
と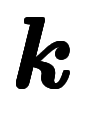 との対応が曖昧になる。
との対応が曖昧になる。
 と
と と書き分けたどころで、他の次元には適応し難い問題が残る。
と書き分けたどころで、他の次元には適応し難い問題が残る。
|



変数定義の多様性を纏めるには、双対関係を記号化すれば良い。
以下に、双対基底を記号化した凌宮数学の逆基底表記をフーリエ変換に適応する。
時間領域におけるフーリエ変換では、
原点から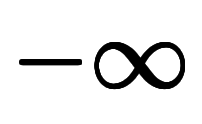 〜
〜 まで任意の時刻までの時間についての積分を行う。
まで任意の時刻までの時間についての積分を行う。
これは、周期を重みとした相加平均と見なせて、時間 が実質上周期
が実質上周期 を意味する。
を意味する。
このため、周波数と周期の関係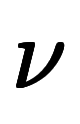

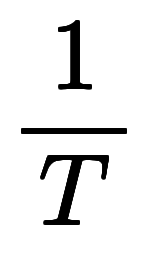 を周波数と時間の関係
を周波数と時間の関係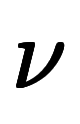

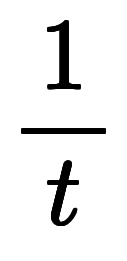 に読み替えられる。
に読み替えられる。
これを式4a・式4bに代入すると、カーネル関数では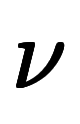


 となって関数の性質が消滅してしまうため、
となって関数の性質が消滅してしまうため、
同時に基底を基底と分かるように
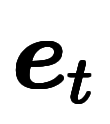 、
、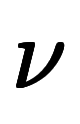

 に書き換えると、式5a・式5bが得られる。
に書き換えると、式5a・式5bが得られる。
式5a 正変換: |


