概要 EditToHeaderToFooter

鉄は約910℃で体心立方構造のα鉄から、面心立方構造のγ鉄に相転移する。
そこで、α鉄に対するγ鉄の密度比を計算せよ、という類の問題があるらしい。

cf: http://pub.maruzen.co.jp/book_magazine/support/cgbukka_pdf/05.pdf

解答例として、密度比が充填率比に等しいとして、構造から一義に計算できる充填率比で代用する方法が挙げられる。
しかしながら、この方法は、α鉄とγ鉄の原子半径が同じことを暗に仮定するため、非現実的な出題である可能性がある。

原子半径の差異、および、充填率と密度の乖離 EditToHeaderToFooter

http://fracmech.me.es.osaka-u.ac.jp/days/staff/kizaiB1.pdf pp.9-10/26より、単位格子中の原子数と格子定数は以下の通り*1。

　　α鉄（フェライト）

　　γ鉄（オーステナイト）

　　結晶構造　　　

　　体心立方格子

　　面心立方格子

　　原子数

　　$$ n_\alpha $$＝2個

　　$$ n_\gamma $$＝4個

　　格子定数　　　

　　$$ a_\alpha $$＝0.287nm

　　$$ a_\gamma $$＝0.358nm

一般に、幾何的には格子定数だけで以下の量が計算できる。

　　α鉄（フェライト）　　

　　γ鉄（オーステナイト）

　　原子間距離

　　$$ d_\alpha $$＝$$ \ffd{\sqrt{3}}{2} $$＝0.249nm

　　$$ d_\gamma $$＝$$ \ffd{\sqrt{2}}{2} $$＝0.253nm

　　原子半径

　　$$ r_\alpha $$＝$$ \ffd{d_\alpha}{2} $$＝0.124nm

　　$$ r_\gamma $$＝$$ \ffd{d_\gamma}{2} $$＝0.127nm

　$$ r^{\circ} $$＝$$ \ffd{r_\gamma}{r_\alpha} $$＝1.018

　　原子体積

　　$$ v_\alpha $$＝0.0161nm³

　　$$ v_\gamma $$＝0.0340nm³

$$ v $$＝$$ n \cdot \ffd43 \pi r^3 $$

　　格子体積

　　$$ V_\alpha $$＝$$ a_\alpha^3 $$＝0.0236nm³

　　$$ V_\gamma $$＝$$ a_\gamma^3 $$＝0.0459nm³

　　充填率

　　$$ f_\alpha $$＝$$ \ffd{v_\alpha}{V_\alpha} $$＝0.680

　　$$ f_\gamma $$＝$$ \ffd{v_\gamma}{V_\gamma} $$＝0.740

　$$ f^{\circ} $$＝$$ \ffd{f_\gamma}{f_\alpha} $$＝1.089

ここで、鉄の原子１個の質量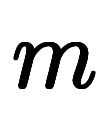$$ m $$と置くと、

　　α鉄（フェライト）

　　γ鉄（オーステナイト）

　　密度

　　$$ \rho_\alpha $$＝$$ \ffd{n_\alpha m}{V_\alpha} $$＝84.6$$ m $$/nm³

　　$$ \rho_\gamma $$＝$$ \ffd{n_\gamma m}{V_\gamma} $$＝87.2$$ m $$/nm³

$$ \rho^{\circ} $$＝$$ \ffd{\rho_\gamma}{\rho_\alpha} $$＝1.030

原子半径が0.124nmと0.127nmと差で0.003nm、比で1.018程度の差異に対し、
充填率と密度は1.089と1.030と、比で$$ \ffd{f^{\circ}}{\rho^{\circ}} $$＝1.056も乖離している。

*1 p11の値を使うともっと大きく異なるが、差の小さい方でも充分な差異が出たため、本稿では差の小さい方で示す。

充填率と密度の乖離と半径の関係 EditToHeaderToFooter

$$ f^{\circ} $$＝$$ \ffd{f_\gamma}{f_\alpha} $$＝$$ \ffd{\ffd{v_\gamma}{V_\gamma}}{\ffd{v_\alpha}{V_\alpha}} $$＝$$ \ffd{\ffd{n_\gamma \cdot \ffd43 \pi r_\gamma^3}{V_\gamma}}{\ffd{n_\alpha \cdot \ffd43 \pi r_\alpha^3}{V_\alpha}} $$＝$$ \ffd{\ffd{n_\gamma}{V_\gamma}r_\gamma^3}{\ffd{n_\alpha}{V_\alpha}r_\alpha^3} $$＝$$ \ffd{\ffd{n_\gamma m}{V_\gamma}r_\gamma^3}{\ffd{n_\alpha m}{V_\alpha}r_\alpha^3} $$＝$$ \ffd{\rho_\gamma r_\gamma^3}{\rho_\alpha r_\alpha^3} $$＝$$ \rho^\circ $$$$ (r^\circ)^3 $$

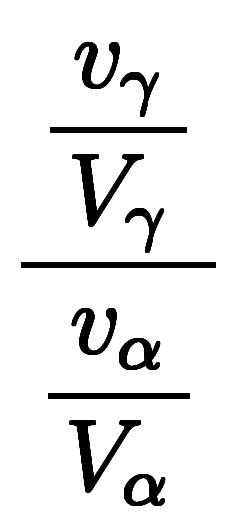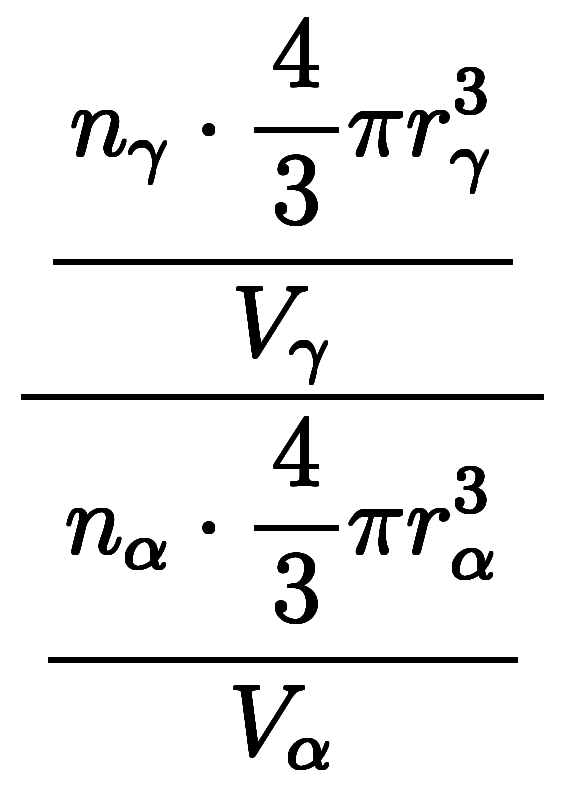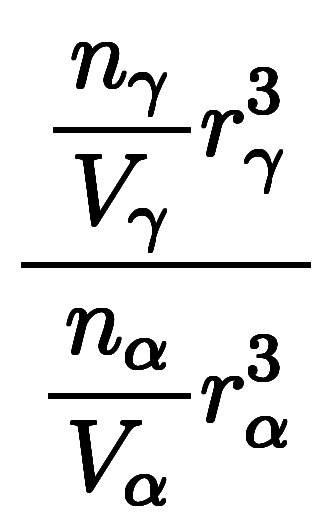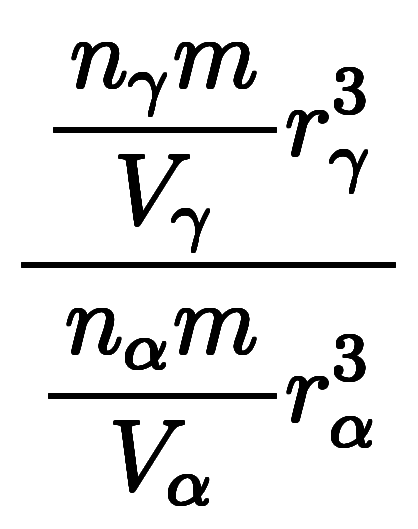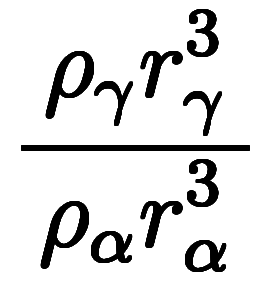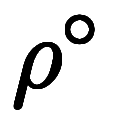
原子半径が変わらない場合は、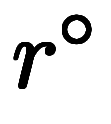$$ r^\circ $$＝1となり、充填率と密度が一致する。
対して、原子半径が変る場合は、充填率と密度の乖離は半径比の三乗で乖離する。
半径比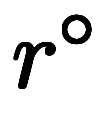$$ r^{\circ} $$＝1.018に対し、充填率と密度の乖離は1.018³＝1.056となる。

注意 EditToHeaderToFooter

γ鉄の格子定数に$$ a_\gamma^\prime $$＝0.364という値も見つかっていて*2、この値を使うと、密度の大きさが逆転する。
比の値が1以上・以下では定性的な違いが生じるため、結論を変える必要があるかもしれない。
γ鉄の格子定数も含め、後日再度調査し、追って加筆する。
file原子半径の温度変化.jpg 1129件 [詳細] file密度の温度変化.jpg 913件 [詳細]
    数学 一覧 検索 最新 バックアップ リンク元   ヘルプ   最終更新のRSS