![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
基底成分表記 のバックアップ(No.2) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
基底成分表記 のバックアップ(No.2) |
基底成分表記 |
通常ベクトルの倍積 | 1次形式 |
通常ベクトルの外積 | 1次形式 |
微小ベクトルの内積 | 1次形式 |
一般的に、通常基底も p ベクトルとして を適用できる。むしろ、通常ベクトルの倍積、外積、内積を先に
を適用できる。むしろ、通常ベクトルの倍積、外積、内積を先に で纏めてから微分形式に応用するのが歴史に沿った手順である。しかし、この手順では
で纏めてから微分形式に応用するのが歴史に沿った手順である。しかし、この手順では が通常基底と微分基底の両方に使われるため、混同が起こる。普通は両系統の基底が同時に登場しないよう、上手く問題を避けているが、これがベクトル解析の授業と微分形式の授業の間に要らぬギャップを作ってしまう。
が通常基底と微分基底の両方に使われるため、混同が起こる。普通は両系統の基底が同時に登場しないよう、上手く問題を避けているが、これがベクトル解析の授業と微分形式の授業の間に要らぬギャップを作ってしまう。
成分基底表記も、元々はこのギャップの橋渡しのために考案した表記で、演算子を に統一しても基底のハイライト表現で十分に区別できる。しかし、3次元を扱う限り、倍積、外積、内積の方が敷居が低いため、今回は混乱を避けるよう一般的に対する演算に
に統一しても基底のハイライト表現で十分に区別できる。しかし、3次元を扱う限り、倍積、外積、内積の方が敷居が低いため、今回は混乱を避けるよう一般的に対する演算に を使わないでおく。
を使わないでおく。



ストークスの定理は、猫式の基底成分表記とベクトル積分演算子で表記すると次のようになる。![\inte[S] d^{-2} \arrb{ \b e_x & \fracstrut \ppd{}{x} \\ \b e_y & \fracstrut \ppd{}{y} \\ \b e_z & \fracstrut \ppd{}{z} } \vx \arrb{ \b e_x & \fracstrut F_x \\ \b e_y & \fracstrut F_y \\ \b e_z & \fracstrut F_z } \sx \arrb{ \b e_x & \fracstrut d y d z \\ \b e_y & \fracstrut d z d x \\ \b e_z & \fracstrut d x d y } $$ \inte[S] d^{-2} \arrb{ \b e_x & \fracstrut \ppd{}{x} \\ \b e_y & \fracstrut \ppd{}{y} \\ \b e_z & \fracstrut \ppd{}{z} } \vx \arrb{ \b e_x & \fracstrut F_x \\ \b e_y & \fracstrut F_y \\ \b e_z & \fracstrut F_z } \sx \arrb{ \b e_x & \fracstrut d y d z \\ \b e_y & \fracstrut d z d x \\ \b e_z & \fracstrut d x d y } $$](./eq/eq-ni-85e8ff1167f55f3278f5e9539e13c142.png) =
=![\inte[R] d^- \arrb{ \b e_x & F_x \\ \b e_y & F_y \\ \b e_z & F_z } \sx \arrb{ \b e_x & d x \\ \b e_y & d y \\ \b e_z & d z } $$ \inte[R] d^- \arrb{ \b e_x & F_x \\ \b e_y & F_y \\ \b e_z & F_z } \sx \arrb{ \b e_x & d x \\ \b e_y & d y \\ \b e_z & d z } $$](./eq/eq-ni-cbd57ae6fc26abcb1418b4fc4d91a758.png)
左辺= | |
= | 通常基底外積を実行 |
= | 通常基底内積を実行 |
= | 微小基底にハイライト |
= | 1次形式 |
= | 外微分演算子の定義より |
= |
|
= | 再び通常基底にハイライト |
= | 通常基底の内積に分解 |
=右辺 |



上の計算途中で、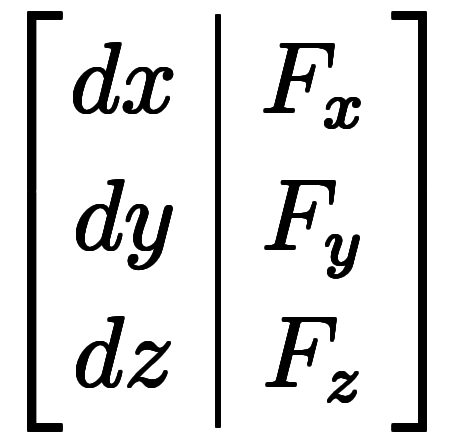 =
=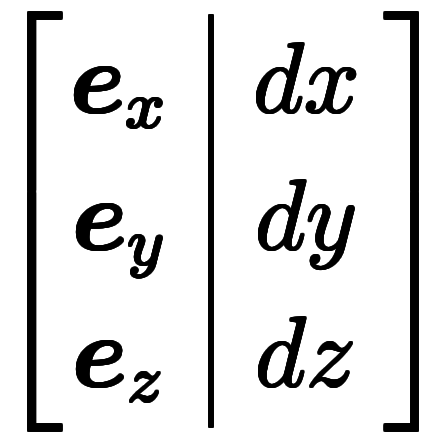

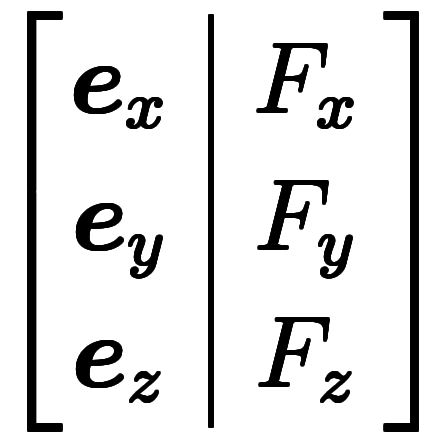 とあるが、注釈にもあるように、微小基底があるため、通常基底の内積を取っても3つ成分ベクトルは混ざることはなく、このような割り込みは可能となる。
とあるが、注釈にもあるように、微小基底があるため、通常基底の内積を取っても3つ成分ベクトルは混ざることはなく、このような割り込みは可能となる。
これを利用して、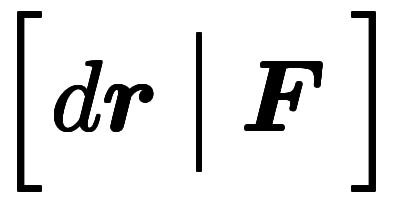 =
=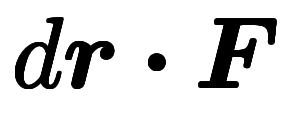 と定義すれば、通常ベクトルの内積と基底成分表記が簡単に行き来できる。もともと基底と成分は積で扱われるため、ベクトルの場合に対し内積を取るのは自然の拡張と言える。
と定義すれば、通常ベクトルの内積と基底成分表記が簡単に行き来できる。もともと基底と成分は積で扱われるため、ベクトルの場合に対し内積を取るのは自然の拡張と言える。
これより、微小基底の3種類の演算は次のように書ける。
1次形式 |
この簡略表記と猫式のベクトル微分演算子により、ストークスの定理は次のように変形できる。![\inte[S] d^{-2} $$ \inte[S] d^{-2} $$](./eq/eq-ni-d36c0a325e9c6b00826f1b515429004c.png)
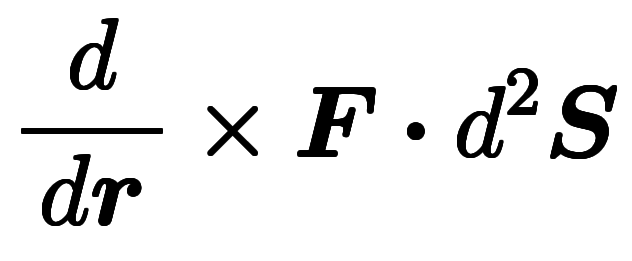 =
=![\inte[R] d^- $$ \inte[R] d^- $$](./eq/eq-ni-3f65dc272ee253de800e757bfcba8cbf.png)
 =
=![\inte[R] d^- $$ \inte[R] d^- $$](./eq/eq-ni-3f65dc272ee253de800e757bfcba8cbf.png)
 =
=![\inte[R] d^- $$ \inte[R] d^- $$](./eq/eq-ni-3f65dc272ee253de800e757bfcba8cbf.png)
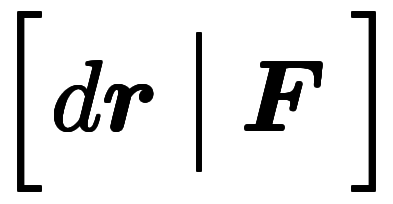 =
=![\inte[R] d^- $$ \inte[R] d^- $$](./eq/eq-ni-3f65dc272ee253de800e757bfcba8cbf.png)
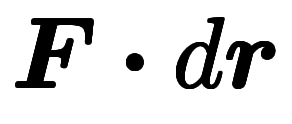
同様に、ガウスの定理は次のように変形できる。![\inte[V] d^{-3} $$ \inte[V] d^{-3} $$](./eq/eq-ni-8b4f7479f4e47aade78a75e11173759c.png)
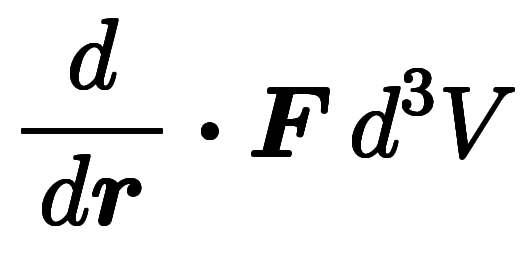 =
=![\inte[S] d^{-2} $$ \inte[S] d^{-2} $$](./eq/eq-ni-d36c0a325e9c6b00826f1b515429004c.png)
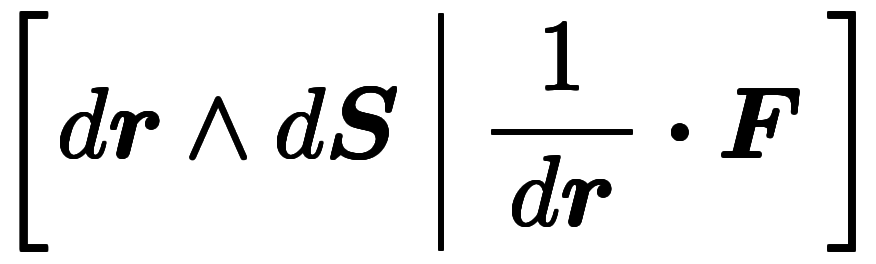 =
=![\inte[S] d^{-2} $$ \inte[S] d^{-2} $$](./eq/eq-ni-d36c0a325e9c6b00826f1b515429004c.png)
 =
=![\inte[S] d^{-2} $$ \inte[S] d^{-2} $$](./eq/eq-ni-d36c0a325e9c6b00826f1b515429004c.png)
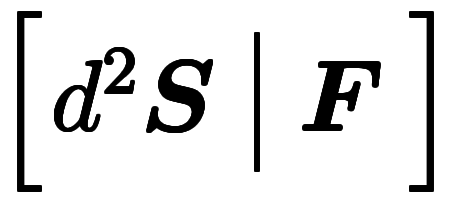 =
=![\inte[S] d^{-2} $$ \inte[S] d^{-2} $$](./eq/eq-ni-d36c0a325e9c6b00826f1b515429004c.png)
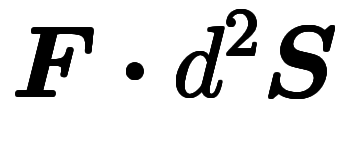



今回は、微分形式を経由して、積分公式を導きいた。ベクトル形の積分公式と微分形式を橋渡しするため独自の表記を用いたが、個々の手順自体は合法的。やってることは、 =
=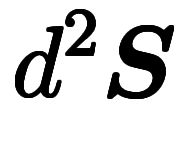 、
、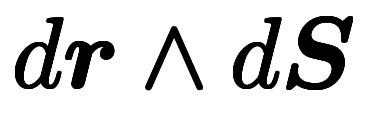 =
= によって微小要素を分解してから、
によって微小要素を分解してから、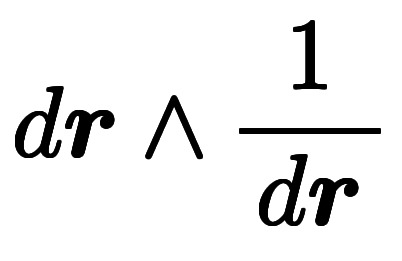 単位で消している。
単位で消している。
これと同じことを、前回は =
=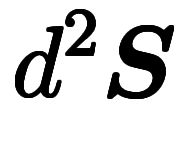 、
、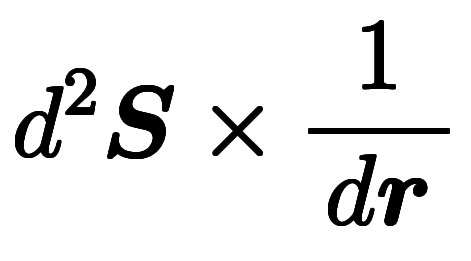 =
= と理解していた。その結果を作り出すために考えたインチキ規則は、微小基底の二項演算を眺めば、成分側の演算手順から基底側の演算手順への変換規則であるの分かる。
と理解していた。その結果を作り出すために考えたインチキ規則は、微小基底の二項演算を眺めば、成分側の演算手順から基底側の演算手順への変換規則であるの分かる。 の演算では、成分が加算項と減算項の2つに分かれ、基底の並びは必ず加算項と一致する。一方で、通常基底と微傷基底の演算を比較すると、成分側の計算が完全に一致する。このため、通常基底として計算して置き、減算項を抜けば、微小基底の基底側の演算結果が出てくる。
の演算では、成分が加算項と減算項の2つに分かれ、基底の並びは必ず加算項と一致する。一方で、通常基底と微傷基底の演算を比較すると、成分側の計算が完全に一致する。このため、通常基底として計算して置き、減算項を抜けば、微小基底の基底側の演算結果が出てくる。
直観的センスとしては、今回は =
=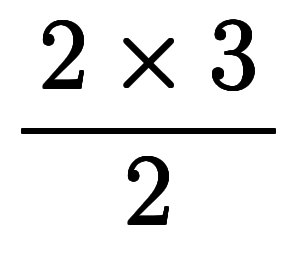 =
=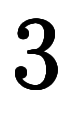 と回りくどいのに対し、前回は
と回りくどいのに対し、前回は =
=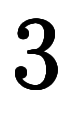 と直接割ってるため、一枚上手と思う。
と直接割ってるため、一枚上手と思う。
微分形式では、1次形式が線積分、2次形式が面積分、3次形式が体積分に対応。3、2、1の次は0。体、面、線の次は点。というわけで、次回、0次形式に対応する「点積分」。