格子ベクトルと逆格子ベクトル EditToHeaderToFooter

結晶構造を扱う諸分野では、
実格子ベクトル$$ \:R $$と逆格子ベクトル$$ \:G $$と呼ばれる概念があり、回折の計算で役立つ。
これらはベクトル解析における双対基底の一つの応用と見なせるため、
双対基底の概念を使えば簡単に理解でき、凌宮の逆基底表記で簡潔に表記できる。

一般的定義 EditToHeaderToFooter

一般に、結晶は３次元の周期性を持ち、３つの基底と３つの整数係数の線形結合で全格子点を表現できる。
これらの基底は、基本並進ベクトルや基本単位ベクトルと呼ばれ、各周期方向の格子点の間隔を表す。
基本単位ベクトルを$$ \:a_1 $$、$$ \:a_2 $$、$$ \:a_3 $$、任意の整数を$$ n_1 $$、$$ n_2 $$、$$ n_3 $$と置くと、
任意の格子点の位置ベクトルである格子ベクトル$$ \:R $$を次のように与えられる：

$$ \:R $$$$ = $$$$ n_1 $$$$ \:a_1 $$$$ + $$$$ n_2 $$$$ \:a_2 $$$$ + $$$$ n_3 $$$$ \:a_3 $$

一般に、基本逆格子ベクトル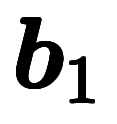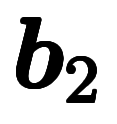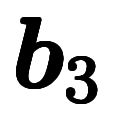$$ \:b_1 $$、$$ \:b_2 $$、$$ \:b_3 $$は、計算法として以下のように定義される*1：

$$ \:b_1 $$$$ = $$$$ 2\pi $$$$ \ffd{\:a_2 \vx \:a_3}{\:a_1 \sx (\:a_2 \vx \:a_3)} $$

$$ \:b_2 $$$$ = $$$$ 2\pi $$$$ \ffd{\:a_3 \vx \:a_1}{\:a_2 \sx (\:a_3 \vx \:a_1)} $$

$$ \:b_3 $$$$ = $$$$ 2\pi $$$$ \ffd{\:a_1 \vx \:a_2}{\:a_3 \sx (\:a_1 \vx \:a_2)} $$

格子ベクトルと同様に、任意の整数を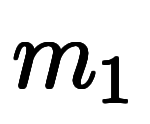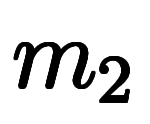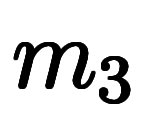$$ m_1 $$、$$ m_2 $$、$$ m_3 $$を用いて、線形結合をもって逆格子ベクトルを定義できる。

$$ \:G $$$$ = $$$$ m_1 $$$$ \:b_1 $$$$ + $$$$ m_2 $$$$ \:b_2 $$$$ + $$$$ m_3 $$$$ \:b_3 $$

逆基底表記による表記 EditToHeaderToFooter

基本逆格子ベクトルの定義から、
基本逆格子ベクトルは対応する基本格子ベクトルの逆基底を$$ 2\pi $$倍したベクトルであると言える。
このため、凌宮数学の逆基底表記を用いると、基本逆格子ベクトルを次のように表記できる：

$$ \:b_1 $$$$ = $$$$ 2\pi $$$$ \ffd{\:a_2 \vx \:a_3}{\:a_1 \sx (\:a_2 \vx \:a_3)} $$$$ \Rightarrow $$$$ 2\pi $$$$ \ffd{1}{\:a_1} $$$$ = $$$$ \ffd{2\pi}{\:a_1} $$

$$ \:b_2 $$$$ = $$$$ 2\pi $$$$ \ffd{\:a_3 \vx \:a_1}{\:a_2 \sx (\:a_3 \vx \:a_1)} $$$$ \Rightarrow $$$$ 2\pi $$$$ \ffd{1}{\:a_2} $$$$ = $$$$ \ffd{2\pi}{\:a_2} $$

$$ \:b_3 $$$$ = $$$$ 2\pi $$$$ \ffd{\:a_1 \vx \:a_2}{\:a_3 \sx (\:a_1 \vx \:a_2)} $$$$ \Rightarrow $$$$ 2\pi $$$$ \ffd{1}{\:a_3} $$$$ = $$$$ \ffd{2\pi}{\:a_3} $$

逆格子ベクトルは、同様に任意整数を係数とする線形結合で与えられる：

$$ \:G $$

$$ = $$$$ m_1 $$$$ \ffd{2\pi}{\:a_1} $$$$ + $$$$ m_2 $$$$ \ffd{2\pi}{\:a_2} $$$$ + $$$$ m_3 $$$$ \ffd{2\pi}{\:a_3} $$

$$ = $$$$ 2\pi $$$$ \Big( $$$$ \ffd{m_1}{\:a_1} $$$$ + $$$$ \ffd{m_2}{\:a_2} $$$$ + $$$$ \ffd{m_3}{\:a_3} $$$$ \Big) $$

基本格子ベクトルや基本逆格子ベクトルは空間的周期性を記述するための物理量であり、
空間的に周期性を記述する物理量と比較すると理解し易い：

時間的周期性空間的周期性
　周期　$$ T $$ 　波長、基本格子ベクトル$$ \:a $$ 
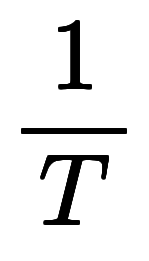　周波数$$ f $$$$ = $$$$ \ffd{1}{T} $$　波数、基本逆格子ベクトル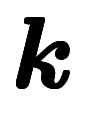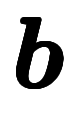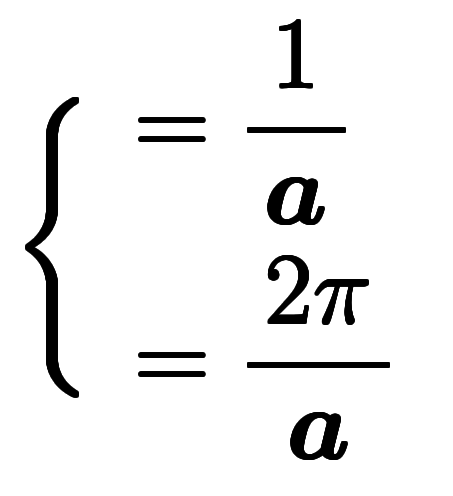$$ \:k $$、$$ \:b $$$$ \Bigg\{\begin{array}{l} = \ffd{1}{\:a} \\ = \ffd{2\pi}{\:a} \end{array} $$
角周波数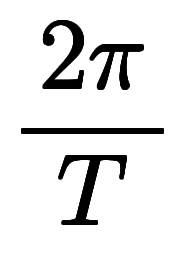$$ \omega $$$$ = $$$$ \ffd{2\pi}{T} $$角波数、

内積 EditToHeaderToFooter

双対基底の性質から、基本格子ベクトルと基本逆格子ベクトルの内積は$$ 2\pi $$または$$ 0 $$になる。

$$ \iro[ao]{\:a_1} $$$$ \iro[ao]{\sx} $$$$ \iro[ao]{\:b_1} $$$$ \iro[ao]{=} $$$$ \iro[ao]{\:a_1} $$$$ \iro[ao]{\sx} $$$$ \iro[ao]{\ffd{2\pi}{\:a_1}} $$$$ \iro[ao]{=} $$$$ \iro[ao]{2\pi} $$

$$ \iro[ak]{\:a_1} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\:b_2} $$$$ \iro[ak]{=} $$$$ \iro[ak]{\:a_1} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\ffd{2\pi}{\:a_2}} $$$$ \iro[ak]{=} $$$$ \iro[ak]{0} $$

$$ \iro[ak]{\:a_1} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\:b_3} $$$$ \iro[ak]{=} $$$$ \iro[ak]{\:a_1} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\ffd{2\pi}{\:a_3}} $$$$ \iro[ak]{=} $$$$ \iro[ak]{0} $$

$$ \iro[ak]{\:a_2} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\:b_1} $$$$ \iro[ak]{=} $$$$ \iro[ak]{\:a_2} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\ffd{2\pi}{\:a_1}} $$$$ \iro[ak]{=} $$$$ \iro[ak]{0} $$

$$ \iro[ao]{\:a_2} $$$$ \iro[ao]{\sx} $$$$ \iro[ao]{\:b_2} $$$$ \iro[ao]{=} $$$$ \iro[ao]{\:a_2} $$$$ \iro[ao]{\sx} $$$$ \iro[ao]{\ffd{2\pi}{\:a_2}} $$$$ \iro[ao]{=} $$$$ \iro[ao]{2\pi} $$

$$ \iro[ak]{\:a_2} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\:b_3} $$$$ \iro[ak]{=} $$$$ \iro[ak]{\:a_2} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\ffd{2\pi}{\:a_3}} $$$$ \iro[ak]{=} $$$$ \iro[ak]{0} $$

$$ \iro[ak]{\:a_3} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\:b_1} $$$$ \iro[ak]{=} $$$$ \iro[ak]{\:a_3} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\ffd{2\pi}{\:a_1}} $$$$ \iro[ak]{=} $$$$ \iro[ak]{0} $$

$$ \iro[ak]{\:a_3} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\:b_2} $$$$ \iro[ak]{=} $$$$ \iro[ak]{\:a_3} $$$$ \iro[ak]{\sx} $$$$ \iro[ak]{\ffd{2\pi}{\:a_2}} $$$$ \iro[ak]{=} $$$$ \iro[ak]{0} $$

$$ \iro[ao]{\:a_3} $$$$ \iro[ao]{\sx} $$$$ \iro[ao]{\:b_3} $$$$ \iro[ao]{=} $$$$ \iro[ao]{\:a_3} $$$$ \iro[ao]{\sx} $$$$ \iro[ao]{\ffd{2\pi}{\:a_3}} $$$$ \iro[ao]{=} $$$$ \iro[ao]{2\pi} $$

このため、$$ \:R $$と$$ \:G $$内積は必ず整数の$$ 2\pi $$倍になる。

$$ \:R $$$$ \sx $$$$ \:G $$$$ = $$$$ 2\pi $$$$ N $$　　ただし、$$ N $$$$ = $$$$ n_1 $$$$ m_1 $$$$ + $$$$ n_2 $$$$ m_2 $$$$ + $$$$ n_3 $$$$ m_3 $$で必ず整数になる

EditToHeaderToFooter
*1 流派によっては$$ 2\pi $$を含ませず、公式に顕わに出す場合もある。
    数学 一覧 検索 最新 バックアップ リンク元   ヘルプ   最終更新のRSS