というか、「算数教育における文章題での加減算の用法の分類」

導入 EditToHeaderToFooter

算数教育において、加算と減算に対して以下のように分類しているらしい。

  • 加算： 合併、増加、求大、減少前推論、逆求大
  • 減算： 求残、求差、求補、求小、増加前推論、増加数推論、減少数推論、逆求小

全部で加算５種、減算８種で、全部で合わせて計13種。
自分は、合併、増加、求差、求補を知っていたが、他は最近教えていただくまでは聞いたことも無かった。
というわけで、理解を兼ねて再整理してみた。

とある加減算の分類 EditToHeaderToFooter

加減算13種の分類は確かに存在するようだが、
残念ながら、ネット上に無料で公開されている資料では、中々定義を確認できなかった。
このため、資料を付きあわせて、定義を勘ぐるしかない。

個人的に一番分かりやすかったのが、中尾氏が作った「文章題バイキング」にある説明である。
http://nakao.yu-nagi.com/kyouzai-viking-bunsyoudai.htm
例文には限定された題材と記述が用いられているため、注目点や相違点が際立っている。

以下が「文章題バイキング」に登場するパターンである。（ほぼ引用、例文の文体に変更あり）

表１： 加減算文章題の分類パターン
演
算		パターン名パターン式例文
条件１条件２質問
加
算		合併Ａ＋Ｂ＝Ｘ林檎がＡ個ある。蜜柑がＢ個ある。全部で何個ある？
増加Ａ＋Ｂ＝Ｘ林檎がＡ個ある。林檎をＢ個貰った。全部で何個ある？
減少前推論Ｘ−Ａ＝Ｂ林檎をＡ個あげた。林檎がＢ個になった。初めに何個あった？
求大Ｘ＝Ａ＋Ｂ林檎がＡ個ある。蜜柑は林檎よりＢ個多い。蜜柑は何個ある？
逆求小Ｘ−Ａ＝Ｂ林檎がＡ個ある。林檎は蜜柑よりＢ個少ない。蜜柑は何個ある？
減
算		求残Ａ−Ｂ＝Ｘ林檎がＡ個ある。林檎をＢ個あげた。何個残っている？
求補Ａ−Ｂ＝Ｘ林檎と蜜柑が全部でＡ個ある。林檎はＢ個ある。蜜柑は何個ある？
求差Ａ−Ｂ＝Ｘ林檎がＡ個ある。蜜柑はＢ個ある。違いは何個？
増加前推論Ｘ＋Ａ＝Ｂ林檎をＡ個貰った。林檎がＢ個になった。初めに何個あった？
減少数推論Ａ−Ｘ＝Ｂ林檎がＡ個あった。あげたらＢ個になった。何個あげた？
増加数推論Ａ＋Ｘ＝Ｂ林檎がＡ個あった。貰ったらＢ個になった。何個貰った？
求小Ｘ＝Ａ−Ｂ林檎がＡ個ある。蜜柑は林檎よりＢ個少ない。蜜柑は何個ある？
求大Ａ−Ｘ＝Ｂ林檎がＡ個ある。林檎は蜜柑よりＢ個多い。蜜柑は何個ある？

解析的分類 EditToHeaderToFooter

一般に、加算Ａ＋Ｂ＝Ｃに関して、Ａを被加数、Ｂを加数、Ｃを和と呼ぶ。
加算自体を和を求める演算と捕らえることができる。
その場合、減法は被加数と加数を求める加法の逆演算と捕らえられる。

表２： 加算と減算の相関関係
加法減算
求和求被加数求加数
Ａ＋Ｂ＝ＣＣ−Ｂ＝ＡＣ−Ａ＝Ｂ

この関係のため、１つの式に意味付けすれば、他の２つの式も自ずと対応した意味が付く。
その対応した意味を並べると、表３が得られる。

ただし、規則性を見出すため、以下の工夫を施した：

  • パターン式は「既知は左辺、未知は右辺」に統一
  • キーとなる変数名には特別の文字を割当
  • 名実になるよう、意味に基づいた仮の系統名を割当（従来の分類名は括弧書き）
表３： 加算と減算の相関関係に基づくパターンの整理*1
 加算減算
求和求被加数求加数
直
和		Ａ＋Ｂ＝ＣＣ−Ｂ＝ＡＣ−Ａ＝Ｂ
求全部求部分求部分
（合併）（求補）（求補）
変
化		増
加		Ａ＋Ｉ＝ＢＢ−Ｉ＝ＡＢ−Ａ＝Ｉ
求増加後求増加前求増加分
（増加）（増加前推論）（増加数推論）
減
少		Ｂ＋Ｄ＝ＡＡ−Ｄ＝ＢＡ−Ｂ＝Ｄ
求減少前求減少後求減少分
（減少前推論）（求残）（減少数推論）
比
較		正
差		Ａ＋Ｐ＝ＢＢ−Ｐ＝ＡＢ−Ａ＝Ｐ
正差求対象正差求基準正差求差分
（求大）（求小）（求差）
負
差		Ｂ＋Ｎ＝ＡＡ−Ｎ＝ＢＡ−Ｂ＝Ｎ
負差求基準負差求対象負差求差分
（逆求小）（逆求大）（求差）
*1 青字は「正思考」を表す

直和 EditToHeaderToFooter

直和に関して、Ａ、Ｂ、Ｃはそれぞれ集合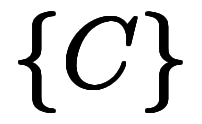$$ \{A\} $$、$$ \{B\} $$、$$ \{C\} $$の要素数に対応している。
集合間には以下の関係が成立していることが立式の前提条件となっている。

表４： 「直和」の前提条件
 直和
同時条件$$ \{A\} $$、$$ \{B\} $$、$$ \{C\} $$は同時に存在
包含条件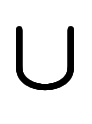$$ \{A\} $$$$ \cup $$$$ \{B\} $$$$ = $$$$ \{C\} $$
排他条件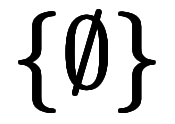$$ \{A\} $$$$ \cap $$$$ \{B\} $$$$ = $$$$ \{\emptyset\} $$$$ {} $$

同時条件は主に次の「変化」との区別である。時間が異なれば「変化」に分類される。
しかし、「合併」という名称は変化を暗示する動作動詞であるため、紛らわしい命名であると思う。
代わりとして、「求補」が「求部分」とも呼ばれるのに因み、「合併」を「求全部」と呼ぶことにする。

包含条件は主に次の「比較」との区別である。包含関係が無ければ「比較」に分類される。
合併の代表的動作である「合わせていくつ」が直結する和集合で条件式を記述しているが、
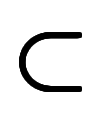
これは$$ \{A\} $$$$ \subset $$$$ \{C\} $$、$$ \{B\} $$$$ \subset $$$$ \{C\} $$と２つの包含関係に分解できる。

排他条件は唯一、加算固有の前提条件である。これが成立しなければ加算を適応できない。
ただ、様々な例文を眺める限り、排他条件が明記されることは滅多にない。
例えば「人は必ず男または女」というような、数学以外の（所謂常識レベルの）知識が回答者に求められる。

合併において、被加数と加数であるＡとＢが対称的である。
このため、減算の求被加数と求加数には違いが無く、同じく求補として分類される。
逆に、合併に関しても被加数と加数を区別せず交換可能で考えないと、この対称性を維持できなくなる。

変化 EditToHeaderToFooter

変化に関して、変化前をＡ、変化後をＢとする。
３番目の量はＡとＢの大小関係で増加分Ｉ（increment）と減少分Ｄ（decrement）に分かれる。
以下の関係が成立していることが立式の前提条件となっている。

表５： 「変化」の前提条件
 増加減少
異時条件$$ \{A\} $$と$$ \{B\} $$は同時には存在しない
包含条件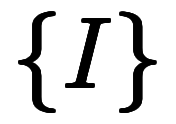$$ \{A\} $$$$ \cup $$$$ \{I\} $$$$ = $$$$ \{B\} $$$$ \{B\} $$$$ \cup $$$$ \{D\} $$$$ = $$$$ \{A\} $$
排他条件$$ \{A\} $$$$ \cap $$$$ \{I\} $$$$ = $$$$ \{\emptyset\} $$$$ \{B\} $$$$ \cap $$$$ \{D\} $$$$ = $$$$ \{\emptyset\} $$

変化が伴う場合、変化の前・後という区別が生じ、前後の大小関係で増加・減少の違いが生じる。
その違いを演算として扱うのが表１や表３に表われる見方である。
すなわち：

  • 増加： 増加前＋増加分＝増加後、増加前＜増加後
  • 減少： 減少前＋減少分＝減少後、増加前＞増加後

表１にあるパターン名でいう「増加」は、その意味から増加した後の量を求める用法であると分かる。
同様に、「求残」とは減少した後の量を求める用法と理解できる。
他の「○○○推論」は、「増加」と「求残」を正思考とする逆思考という考え方に由来する命名に思える。

増加・減少の違いを演算で表現する他に、量の方で表現する見方もできる。
それが後に習う負数を用いた用法となる。

  • 変化： 変化前＋変化分＝変化後
    • 変化分＞０： 増加前＜増加後
    • 変化分＝０： 増加前＝増加後
    • 変化分＞０： 増加前＞増加後

変化と増加・減少を纏めると表５のようになる。
ここで、変化分Δ＝Ｉ＝−Ｄという関係が成り立つ。

表６： 負の概念に基づく変化と増加・減少のパターンの整理
 加算減算
求和求被加数求加数
変
化		 Ａ＋Δ＝ＢＢ−Δ＝ＡＢ−Ａ＝Δ
求変化後求変化前求変化分
   
 増
加		Ａ＋Ｉ＝ＢＢ−Ｉ＝ＡＢ−Ａ＝Ｉ
求増加後求増加前求増加分
（増加）（増加前推論）（増加数推論）
減
少		Ａ＋(−Ｄ)＝ＢＢ−(−Ｄ)＝ＡＢ−Ａ＝(−Ｄ)
求減少後求減少前求減少分
（求残）（減少前推論）（減少数推論）

なるほど。増加・減少での所謂「正思考」とは、増加・減少の統合を見据えた見方と見受ける。
つまり、時間の流れに沿って、変化前と変化分から変化後を想像する思考を正としているように見える。

比較【執筆中】 EditToHeaderToFooter

比較に関して、小さい量をＡ、大きい量をＢとする。
小さい量を基準をする正的な差をＰ (positive)、大きい量を基準とする負的な差をＮ (negative)とする。
「大きい」「多い」で問うのが正差、逆に「小さい」「少ない」で問うのが負差と考えてよい。
以下の関係が成立していることが立式の前提条件となっている。

表７： 「比較」の前提条件
 正差負差
時間条件　（問わない）
排他条件１$$ \{A\} $$$$ \cap $$$$ \{B\} $$$$ = $$$$ \{\emptyset\} $$
排他条件２$$ \{A\} $$$$ \cap $$$$ \{P\} $$$$ = $$$$ \{\emptyset\} $$$$ \{A\} $$$$ \cap $$$$ \{N\!\} $$$$ = $$$$ \{\emptyset\} $$

比較の場合、直和や変化とは異なり、時間の概念を問わない。
その代わり、直和の包含条件がもう一つの排他条件になり、式に登場する３つの量が互いに排他的になる*2。
そして、解くためには$$ \{A\} $$と$$ \{B\} $$間の対応関係を考える必要があるのが特徴である。

対応を具体的に考えるため、具体物で表現しうる$$ \{A\} $$と$$ \{B\} $$が既知である必要がある。
差分を求める減算が「正思考」として考えるのは、どうもこの対応ありきの見方が理由のように見える。

正差・負差を演算で表現する他に、量の方で表現する見方もできる。
それが後に習う負数を用いた用法となる。

  • 比較： 対象−基準＝差分
    • 差分＞０：　対象＞基準
    • 差分＝０：　対象＝基準
    • 差分＜０：　対象＜基準
表８： 負の概念に基づく比較と正差・負差のパターンの整理
 加算減算
求和求被加数求加数
比
較		 Ａ＋Δ＝ＢＢ−Δ＝ＡＢ−Ａ＝Δ
求対象求基準求差分
   
 増
加		Ａ＋Ｐ＝ＢＢ−Ｐ＝ＡＢ−Ａ＝Ｐ
正差求対象正差求基準正差求差分
（求大）（求小）（求差）
減
少		Ａ＋(−Ｎ)＝ＢＢ−(−Ｎ)＝ＡＢ−Ａ＝(−Ｎ)
負差求対象負差求基準負差求差分
（逆求大）（逆求小）（求差）

【執筆中】

*2 負差の場合は差の具現化した際には、排他的でなくす考え方も可能である。それは後述する。

参考文献 EditToHeaderToFooter
    数学 一覧 検索 最新 バックアップ リンク元   ヘルプ   最終更新のRSS