導入 


算数教育において、加算と減算に対して以下のように分類しているらしい。- 加算: 合併、増加、求大、減少前推論、逆求大
- 減算: 求残、求差、求補、求小、増加前推論、増加数推論、減少数推論、逆求小
全部で加算5種、減算8種で、全部で合わせて計13種。
自分は、合併、増加、求差、求補を知っていたが、他は最近教えていただくまでは聞いたことも無かった。
というわけで、理解を兼ねて再整理してみた。
とある加減算の分類 


加減算13種の分類は確かに存在するようだが、
残念ながら、ネット上に無料で公開されている資料では、中々定義を確認できなかった。
このため、資料を付きあわせて、定義を勘ぐるしかない。個人的に一番分かりやすかったのが、中尾氏が作った「文章題バイキング」にある説明である。
http://nakao.yu-nagi.com/kyouzai-viking-bunsyoudai.htm
例文には限定された題材と記述が用いられているため、注目点や相違点が際立っている。
以下が「文章題バイキング」に登場するパターンである。(ほぼ引用、例文の文体に変更あり)
|*演
算|*パターン名|*パターン式*1|* |*例文 |< |< |t=:加
算 | 合併 | A+B=X | 林檎がA個ある。 | 蜜柑がB個ある。 | 全部で何個ある? |
| 増加 | A+B=X | 林檎がA個ある。 | 林檎をB個貰った。 | 全部で何個ある? |
| 求大 | X=A+B | 林檎がA個ある。 | 蜜柑は林檎よりB個多い。 | 蜜柑は何個ある? |
| 減少前推論 | X−A=B | 林檎をA個あげた。 | 林檎がB個になった。 | 初めに何個あった? |
| 逆求小 | X−A=B | 林檎がA個ある。 | 林檎は蜜柑よりB個少ない。 | 蜜柑は何個ある? |
減
算 | 求残 | A−B=X | 林檎がA個ある。 | 林檎をB個あげた。 | 何個残っている? |
| 求補 | A−B=X | 林檎と蜜柑が全部でA個ある。 | 林檎はB個ある。 | 蜜柑は何個ある? |
| 求差 | A−B=X | 林檎がA個ある。 | 蜜柑はB個ある。 | 違いは何個? |
| 求小 | X=A−B | 林檎がA個ある。 | 蜜柑は林檎よりB個少ない。 | 蜜柑は何個ある? |
| 増加前推論 | X+A=B | 林檎をA個貰った。 | 林檎がB個になった。 | 初めに何個あった? |
| 減少数推論 | A−X=B | 林檎がA個あった。 | あげたらB個になった。 | 何個あげた? |
| 増加数推論 | A+X=B | 林檎がA個あった。 | 貰ったらB個になった。 | 何個貰った? |
| 求大 | A−X=B | 林檎がA個ある。 | 林檎は蜜柑よりB個多い。 | 蜜柑は何個ある? |
加
算 | 合併 | A+B=X | 林檎がA個ある。 | 蜜柑がB個ある。 | 全部で何個ある? |
|---|
| 増加 | A+B=X | 林檎がA個ある。 | 林檎をB個貰った。 | 全部で何個ある? |
|---|
| 減少前推論 | X−A=B | 林檎をA個あげた。 | 林檎がB個になった。 | 初めに何個あった? |
|---|
| 求大 | X=A+B | 林檎がA個ある。 | 蜜柑は林檎よりB個多い。 | 蜜柑は何個ある? |
|---|
| 逆求小 | X−A=B | 林檎がA個ある。 | 林檎は蜜柑よりB個少ない。 | 蜜柑は何個ある? |
|---|
減
算 | 求残 | A−B=X | 林檎がA個ある。 | 林檎をB個あげた。 | 何個残っている? |
|---|
| 求補 | A−B=X | 林檎と蜜柑が全部でA個ある。 | 林檎はB個ある。 | 蜜柑は何個ある? |
|---|
| 求差 | A−B=X | 林檎がA個ある。 | 蜜柑はB個ある。 | 違いは何個? |
|---|
| 増加前推論 | X+A=B | 林檎をA個貰った。 | 林檎がB個になった。 | 初めに何個あった? |
|---|
| 減少数推論 | A−X=B | 林檎がA個あった。 | あげたらB個になった。 | 何個あげた? |
|---|
| 増加数推論 | A+X=B | 林檎がA個あった。 | 貰ったらB個になった。 | 何個貰った? |
|---|
| 求小 | X=A−B | 林檎がA個ある。 | 蜜柑は林檎よりB個少ない。 | 蜜柑は何個ある? |
|---|
| 逆求大 | A−X=B | 林檎がA個ある。 | 林檎は蜜柑よりB個多い。 | 蜜柑は何個ある? |
|---|
表1のパターン式では、AとBが既知、Xが未知を表す。
解析的分類 


一般に、加算A+B=Cに関して、Aを被加数、Bを加数、Cを和と呼ぶ。
加算自体を和を求める演算と捕らえることができる。
その場合、減法は被加数と加数を求める加法の逆演算と捕らえられる。
その場合、減算は被加数または加数を求める加法の逆演算と考えられる*2。| 加法 | 減算 |
|---|
| 求和 | 求被加数 | 求加数 |
|---|
| A+B=C | C−B=A | C−A=B |
この関係のため、1つの式に意味付けすれば、他の2つの式も自ずと対応した意味が付く。
その対応した意味を並べると、表3が得られる。
この関係のため、1つの式に意味を付ければ、他の2つの式も自ずと対応した意味が付く。
表1のパターンに対し、意味の対応に着目して整理すると表3が得られる。
ただし、規則性を見出すため、以下の工夫を施した:- パターン式は「既知は左辺、未知は右辺」に統一
- キーとなる変数名には特別の文字を割当
- パターン式は「既知は左辺、未知は右辺」に統一した。
- 正思考を青字で明示した。
- キーとなる変数名には特別の文字を当てた。
- 名実になるよう、用法に基づいた仮の系統名を当てた(従来のパターン名は括弧書きとした)。
| 表3: 加算と減算の相関関係に基づくパターンの整理 |
|---|
| 表3: 加算と減算の相関関係に基づくパターンの整理 |
|---|
集合 


集合に関して、A、B、Cはそれぞれ集合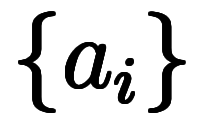 、
、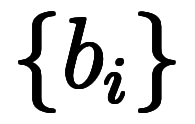 、
、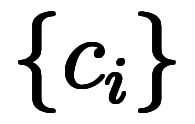 の要素数に対応している。
の要素数に対応している。
集合間には以下の関係が成立していることが立式の前提条件となっている。
同時条件は主に次の「変化」との区別である。時間が異なれば「変化」に分類される。
しかし、「合併」という名称は変化を暗示する動作動詞であるため、紛らわしい命名であると思う。
代わりとして、「求補」が「求部分」とも呼ばれるのに因み、「合併」を「求全部」と呼ぶ。
包含条件は主に次の「比較」との区別である。包含関係が無ければ「比較」に分類される。
合併の代表的動作である「合わせていくつ」が直結する和集合で条件式を記述しているが、
これは
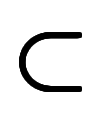
 、
、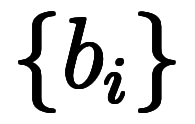

 と2つの包含関係に分解できる。
と2つの包含関係に分解できる。
排他条件は唯一、加算固有の前提条件である。これが成立しなければ加算を適応できない。
ただ、様々な例文を眺める限り、排他条件が明記されることは滅多にない。
例えば「人は必ず男または女」というような、数学以外の(所謂常識レベルの)知識が回答者に求められる。
ただ、実際問題、排他条件が明記されない場合も多々ある。
例えば「人は必ず男または女」というような、数学以外の常識ないし他教科の知識が回答者に求められる*4。
合併において、被加数と加数であるAとBが対称的である。
このため、減算の求被加数と求加数には違いが無く、同じく求補として分類される。
逆に、合併に関しても被加数と加数を区別せず交換可能で考えないと、この対称性を維持できなくなる。
包含条件は主に「比較」との区別である。包含関係が無ければ「比較」に分類される。
以上の排他条件と包含条件が合わせば、集合としての直和演算が満たされることになる。
同時条件は主に「変化」との区別である。時間が異なれば「変化」に分類される。
しかし、「合併」という名称は変化を暗示する動作動詞であるため、
系統名としては「求補」が「求部分」とも呼ばれるのを流用し、「合併」を「求全部」と呼ぶことにする。
直和で注目すべき現象は、減算の求被加数と求加数が区別されずに、求部分(求補)として纏められていることである。
このため、求全部(合併)においても、被加数と加数であるAとBが対称的で同一視しなければ、不整合が起きてしまう。
便宜上、斜体の 、
、 、
、 を集合記号とし、立体のA、B、Cをそれぞれ対応する集合の要素数とする。例えば、A= #
を集合記号とし、立体のA、B、Cをそれぞれ対応する集合の要素数とする。例えば、A= # そして、その常識が往々世界の非常識で、誤りを含む場合も稀に良くある。
そして、その常識が往々世界の非常識で、誤りを含む場合も稀に良くある。
変化 


変化に関して、変化前をA、変化後をB、AとBの大小関係で増加分I(increment)と減少分D(decrement)に分かれる。
以下の関係が成立していることが立式の前提条件となっている。- 異時条件:
- 排他条件:
変化に関して、変化前をA、変化後をBと置く。
3番目の量はAとBの大小関係に応じて、増加分I(increment)または減少分D(decrement)と置く。
そうすると、変化における立式の前提条件が表5のように纏められる。| 異時条件 |  と と は同時には存在しない は同時には存在しない |
|---|
排他条件と包含条件は直和と同じである。
直和に対し時間の概念が加わったのが変化(増加、求残、増加前推論、増加数推論、減少前推論、減少数推論)と捕えて良い。
変化が伴う場合、変化の前・後という区別が生じ、前後の大小関係で増加・減少の違いが生じる。
その違いを演算として扱うのが表1や表3の見方である。- 増加: 増加前<増加後、増加前+増加分=増加後
- 減少: 増加前>増加後、減少前−減少分=減少後
表1にあるパターン名でいう「増加」は、その意味から増加した後の量を求める用法であると分かる。
同様に、「求残」とは減少した後の量を求める用法と理解できる。
他の「○○○推論」は、「増加」と「求残」を正思考とする逆思考という考え方に由来する命名と理解できる。
増加・減少の違いを演算で表現する他に、量の方で表現する見方もできる。
それが後に習う負数を用いた用法となる。- 変化: 変化前+変化分=変化後
- 変化分>0: 増加前<増加後
- 変化分=0: 増加前=増加後
- 変化分>0: 増加前>増加後
変化と増加・減少を纏めると表6のようになる。
ここで、変化分ΔはΔ=IまたはΔ=−Dという関係が成り立つ。
負号の関係上、求減少後と求減少前(求残と減少前推論)の場所を交換し、求減少分(減少数推論)の被減数と減数を逆にした。| 表6: 負の概念に基づく変化と増加・減少のパターンの整理 |
|---|
減
少 | A+(−D)=B | B−(−D)=A | B−A=(−D) |
|---|
表6を見ると、増加・減少での所謂「正思考」とは、増加・減少の統合を見据えているようと思える。
つまり、時間の流れに沿って、変化前と変化分を既知とし、変化後を想像する思考を正としている。
被加数と加数の対称性に関しては、AとΔの意味が異なるため、非対称と言える。
そして、算数においては、変化前+変化分の順番に統一されているように見える。
さらに、物理学など科学分野でも習慣として、この順番で書かれる場合が多い。
比較 


比較に関して、基準となる量をA、対象となる量をBとする。
小さい量を基準をする正的な差を正差P (positive)、大きい量を基準とする負的な差を負差N (negative)とする。
「大きい」「多い」「高い」で問うのが正差、逆に「小さい」「少ない」「低い」で問うのが負差と考えて良い。
以上のように置くと、比較における立式の前提条件が表7のように纏められる。
参考文献 


比較では時間の有無を問わない。
時間の概念があっても、1対1対応が見いだせる場合は、比較と見なされる。
ところが、1対1対応により排他条件を包含条件に変換する必要があるため、対応関係が曖昧な場合が考えられる。
比較では差分を求める減算を正思考とされる。これが直和や変化との大きな違いである。
これに関して、1対1対応を具体的に考える際、具体物で表現しうる対象 と基準
と基準 が必要であると考えられる。
が必要であると考えられる。
特に負差自体が抽象的で、絵で具現化にしにくい。
正差・負差を演算で表現する他に、量の方で表現する見方もできる。
それが後に習う負数を用いた用法となる。- 比較: 対象−基準=差分
- 差分>0: 対象>基準
- 差分=0: 対象=基準
- 差分<0: 対象<基準
ここで、差分ΔはΔ=PまたはΔ=−Nという関係が成り立つ。
負号の関係上、負差求対象と負差求基準(求小と逆求小)の場所を交換し、負差求差分の被減数と減数を逆にした。| 表8: 負の概念に基づく比較と正差・負差のパターンの整理 |
|---|
負
差 | A+(−N)=B | B−(−N)=A | B−A=(−N) |
|---|
表8を見ると、求大・求小・逆求大・逆求小という分類は、正差・負差の統合を見据えているようと思える。
これで、「大」というのは正差が与えられる問題で、「小」というのは負差が与えられる問題と整理できる。
また、無印の求大・求小は基準が与えられる問題で、「逆」が着くのは対象が与えられる問題と整理できる。
これらに対し、「求差」には正差と負差を区別しない。
正差だけを答えさせる場合*5、 対象と正差の両方を答えさせる場合*6が全て求差に含まれる。
現時点では負差の問答例を確認できてないが、負差は正差より難しいらしい*7。
おまけ:外延量と内包量 


連続量について、「合併」が成り立つ量を外延量、成り立たない量を「内包量」と呼ぶ分類がある*8。
「合併」に限定している時点で、下記の変化や比較の話では区別できない分類と言える。
例えば、速度は内包量に分類されるが、比較が該当する相対速度の文脈では加減算が成り立つ。
直和条件は問題に依存するため、量だけで外延量と内包量に一般化するのは限界がある。
例えば、核反応有無で質量に関する直和条件が変わるため、一概に質量が外延量と言えなくなる。
このため、外延量と内包量は小学校限りなど条件を絞った使い方をされることに注意する必要がある。
まとめ 


これまで、算数の界隈で分類される13種の加減算の意味について再整理してみた。
その結果、意味を掘り下げると、3×5種類の用法として整列できた。
意味の命名に関しては、負の概念に基づいた統合を見据えている面も伺えた。
一方で、分類の判定条件として、時間の概念や1対1対応の有無を縦軸に用いた。
これらの判断は主観に基づくため、客観的に判断できないという問題がある。
ここでは、分類の整理を目的とするため、その良し悪しについては議論しない。
最後に、やってみて思ったのだが、これは「意味分類」というより「用法分類」かと。
参考 


リンク 


この記事は凌宮数学の本記事ではありません。
この記事に関する議論は以下でお願いします。
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)






 、
、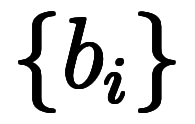 、
、 の要素数に対応している。
の要素数に対応している。 、
、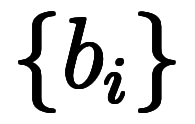 、
、 は同時に存在
は同時に存在
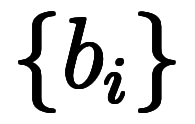




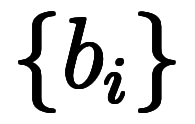

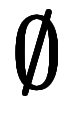



 、
、 、
、 の要素数とすると *3、
の要素数とすると *3、



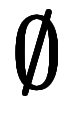






 、
、 、
、 は同時に存在
は同時に存在

 、
、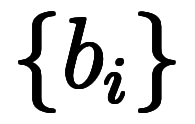

 と2つの包含関係に分解できる。
と2つの包含関係に分解できる。




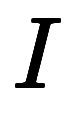









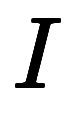







 と
と は同時には存在しない
は同時には存在しない




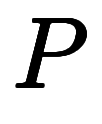

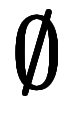




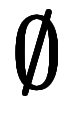




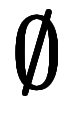



 と基準
と基準 が必要であると考えられる。
が必要であると考えられる。










