![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
指数対数の合成関数の無限級数展開 のバックアップ(No.16) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
指数対数の合成関数の無限級数展開 のバックアップ(No.16) |
設問 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
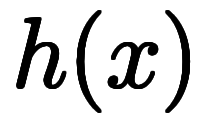

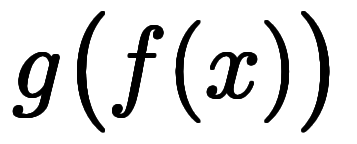 とすると、指数計算により
とすると、指数計算により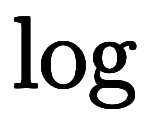 と
と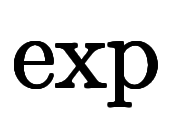 が打消し、簡単な式になる:
が打消し、簡単な式になる:
|
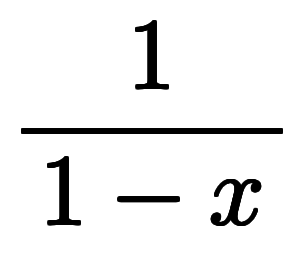 をデーラー展開すると、係数が全て1の級数が得られる。
をデーラー展開すると、係数が全て1の級数が得られる。
| ただし、成立するためには、収束条件 |
一方で、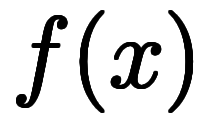 と
と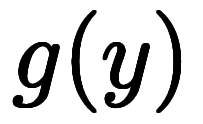 を級数展開しても
を級数展開しても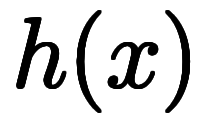 の級数展開が求まる:
の級数展開が求まる:
| 一般に、 |
| 一般に、 |
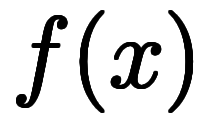 を
を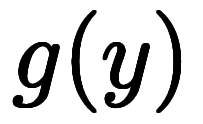 に代入して:
に代入して:
|
よって、上で求めた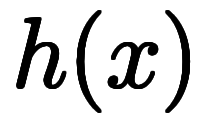

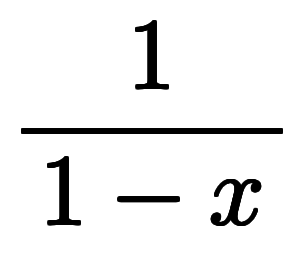 と合わせて、次の等式が成り立つことになる。
と合わせて、次の等式が成り立つことになる。
|
ここで係数比較をすると、任意の

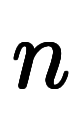

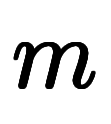 について
について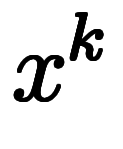 の係数が1でなければならない結論に至る。
の係数が1でなければならない結論に至る。
この関係式は指数・対数、そしてテーラー展開を経由しているが、単なる級数展開でも導けるはず。
しかし、無限級数の入子が含まれているため、簡単には導けない。
したがって、問題:
指数・対数を経由せずに |



問題は係数の証明であるため、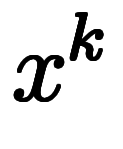 を作るべく、
を作るべく、
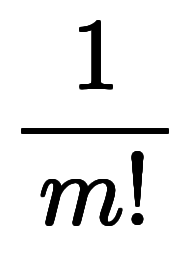


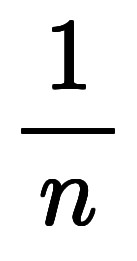
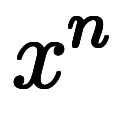
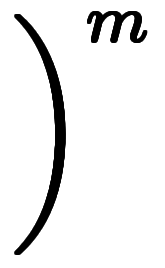 を展開する。
を展開する。
雰囲気を掴めるため、とりあえず具体的に展開し、係数や指数の流れを追う。
|
この展開からは、ざっくり以下のことが読み取れる:
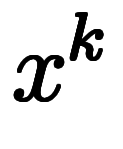 は
は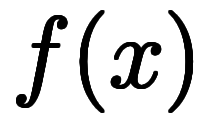 の展開に由来する
の展開に由来する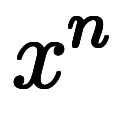 の積で構成される
の積で構成される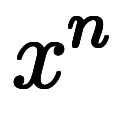 に対応した
に対応した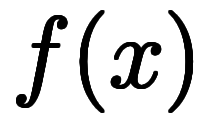 由来の
由来の が係数の因子に含まれる
が係数の因子に含まれる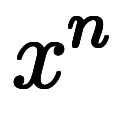 の数、つまり
の数、つまり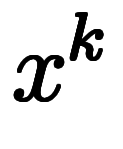 の分割数に対応する
の分割数に対応する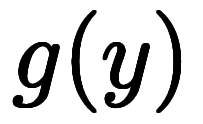 の展開に由来の
の展開に由来の が係数の因子に含まれる
が係数の因子に含まれるまとめると、各項は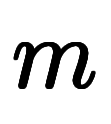 個の
個の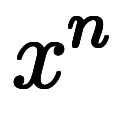 と、
と、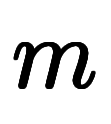 個の
個の と、1つの
と、1つの からなる。
からなる。
このため、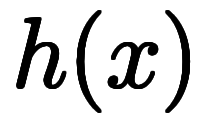 をこれらの因子で直接記述できる。
をこれらの因子で直接記述できる。
|
分割数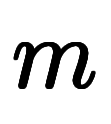 が同じでも分割の仕方が異なる項が存在するため、添字
が同じでも分割の仕方が異なる項が存在するため、添字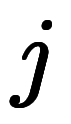 を作って区別することにした。
を作って区別することにした。
また、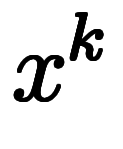 の分割であるため、
の分割であるため、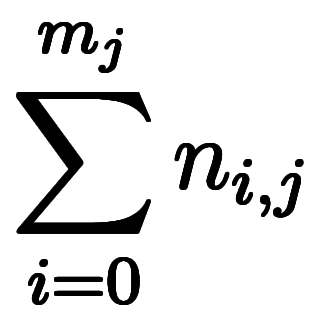

 という関係が成り立ち、
という関係が成り立ち、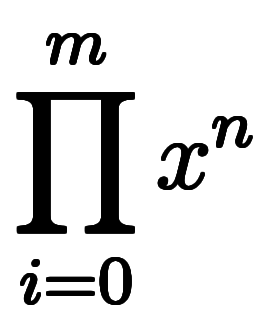

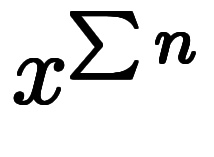

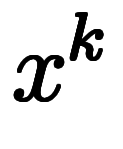 と変形できる。
と変形できる。
よって:
|



以上で、項を区別するために添字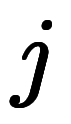 を導入したのは良いが、その上限はまだ知らない。
を導入したのは良いが、その上限はまだ知らない。
以下では、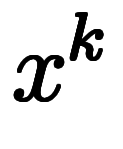 の分割について調べ、
の分割について調べ、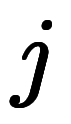 の上限を決定する。
の上限を決定する。
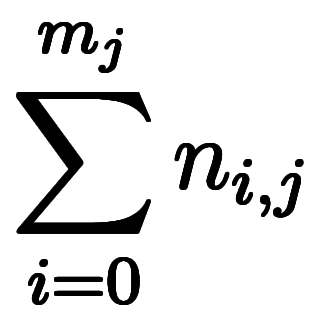

 の関係のため、
の関係のため、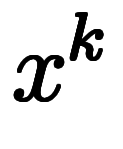 の分割は、
の分割は、 の加数分解と等価である。
の加数分解と等価である。
例えば の場合では、
の場合では、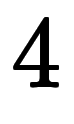 を以下の8通りに分解できる:
を以下の8通りに分解できる:
表1:  の場合の加数分解 の場合の加数分解 | |||
|---|---|---|---|
| 加数分解 | 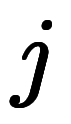 | ![[n_{i,j}] $$ [n_{i,j}] $$](./eq/eq-ni-800f5ef6a513c779ca2cb9f98db6e570.png) | 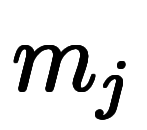  ![\dim[n_{i,j}] $$ \dim[n_{i,j}] $$](./eq/eq-ni-040c91f32ba3d92d57596b5427bb31c7.png) |
 | 1 | ![[4] $$ [4] $$](./eq/eq-ni-c29b8876a475c3670a3c12b9f86f83cd.png) |  |
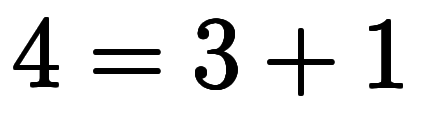 | 2 | ![[3, 1] $$ [3, 1] $$](./eq/eq-ni-bc85cb1ca723579e3620fd58f0f81c6e.png) | 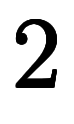 |
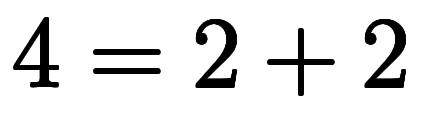 | 3 | ![[2, 2] $$ [2, 2] $$](./eq/eq-ni-cb0d829508e9fe594a58bea7221afebe.png) | 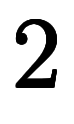 |
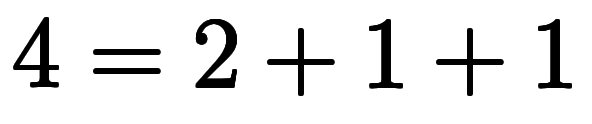 | 4 | ![[1, 1, 1] $$ [1, 1, 1] $$](./eq/eq-ni-6c8b1ef6d34ffe22ff722f5e384139ee.png) | 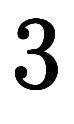 |
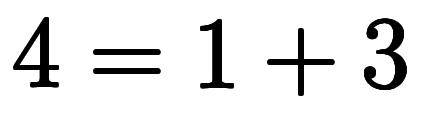 | 5 | ![[1, 3] $$ [1, 3] $$](./eq/eq-ni-c911ba0bf98ba221800ba849d25a3521.png) | 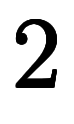 |
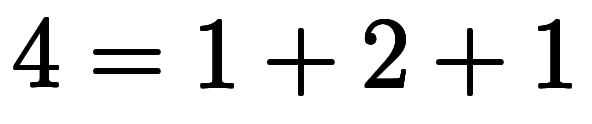 | 6 | ![[1, 2, 1] $$ [1, 2, 1] $$](./eq/eq-ni-8c5f162f7cb021763d4f79db6659fbb4.png) | 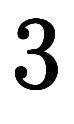 |
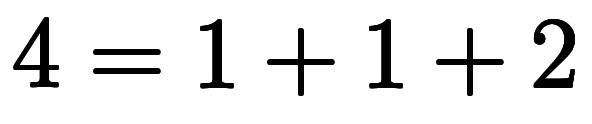 | 7 | ![[1, 1, 2] $$ [1, 1, 2] $$](./eq/eq-ni-a5219a4f32bb9b06d4631505d37c8383.png) | 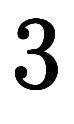 |
 | 8 | ![[1, 1, 1, 1] $$ [1, 1, 1, 1] $$](./eq/eq-ni-bdee9a930a273f9def272529f48c9ba9.png) | 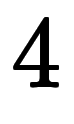 |
また、冪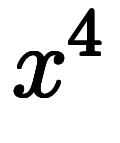 は4つの
は4つの の積を意味するが、その分割は次式の「
の積を意味するが、その分割は次式の「 」に「
」に「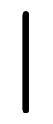 」を入れて区切る操作に等しい。
」を入れて区切る操作に等しい。
|
それぞれの「 」について「
」について「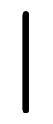 」を「入れる」または「入れない」の
」を「入れる」または「入れない」の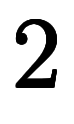 択であるため、
択であるため、
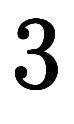 ヵ所であれば
ヵ所であれば 通り出来て、表1の
通り出来て、表1の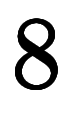 個の項に対応する。
個の項に対応する。
一般化すると、 個の
個の であれば、
であれば、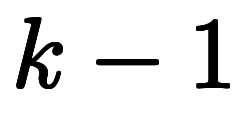 ヶ所に「
ヶ所に「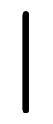 」を入れるため、全部で
」を入れるため、全部で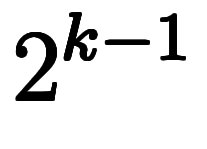 個の項が出来る。
個の項が出来る。
これが項を区別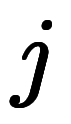 の上限となる。
の上限となる。
したがって:
|
以上より、与題は次と等価であると言える:
|






以上では、とりあえず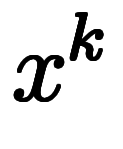 の積和型を作り、係数を抽出できた。
の積和型を作り、係数を抽出できた。
しかし、この総乗もまた厄介なもので、あまり扱いたくはない。
そこで、総乗を回避するべく、 についての漸化式を見いだし、数学的帰納法で攻めることにする。
についての漸化式を見いだし、数学的帰納法で攻めることにする。
項数が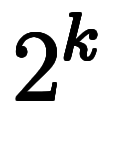 であるため、
であるため、 が増えるごとに項数が2倍になる。
が増えるごとに項数が2倍になる。
このため、漸化式を作るには、 の各項に対し
の各項に対し の項を2つ対応させる必要がある。
の項を2つ対応させる必要がある。
「





 」のような分割について、
」のような分割について、
分割しないことを表す「 」を「
」を「 」、分割することを表す「
」、分割することを表す「 」を「
」を「 」に符号化すると、
」に符号化すると、
分割を 桁の2進数
桁の2進数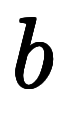 で表すことができる。
で表すことができる。
例えば、 の場合は次のようになる。
の場合は次のようになる。
| 表2: 分割の符号化 | |||||
|---|---|---|---|---|---|
| 加数分解 | 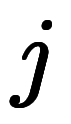 | ![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png) |  分割表現 分割表現 | 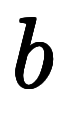 | 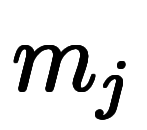  ![\dim[n_{i,j}] $$ \dim[n_{i,j}] $$](./eq/eq-ni-040c91f32ba3d92d57596b5427bb31c7.png) |
 | 1 | ![[4] $$ [4] $$](./eq/eq-ni-c29b8876a475c3670a3c12b9f86f83cd.png) |        | 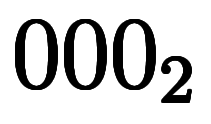 |  |
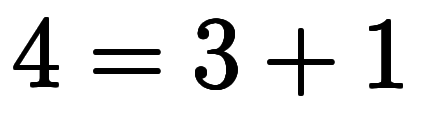 | 2 | ![[3, 1] $$ [3, 1] $$](./eq/eq-ni-bc85cb1ca723579e3620fd58f0f81c6e.png) |        | 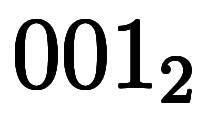 |  |
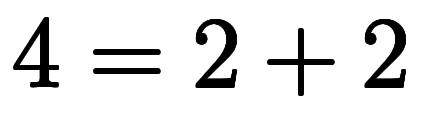 | 3 | ![[2, 2] $$ [2, 2] $$](./eq/eq-ni-cb0d829508e9fe594a58bea7221afebe.png) |        | 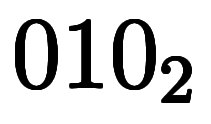 | 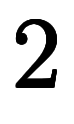 |
 | 4 | ![[2, 1, 1] $$ [2, 1, 1] $$](./eq/eq-ni-d370a482ea47deface2cd97d32d2f52c.png) |        | 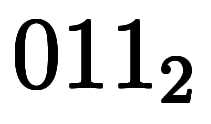 | 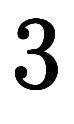 |
 | 5 | ![[1, 3] $$ [1, 3] $$](./eq/eq-ni-c911ba0bf98ba221800ba849d25a3521.png) |        | 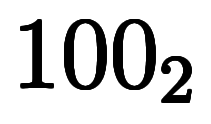 | 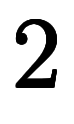 |
 | 6 | ![[1, 2, 1] $$ [1, 2, 1] $$](./eq/eq-ni-8c5f162f7cb021763d4f79db6659fbb4.png) |        | 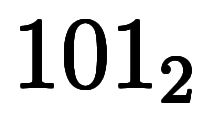 | 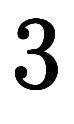 |
 | 7 | ![[1, 1, 2] $$ [1, 1, 2] $$](./eq/eq-ni-a5219a4f32bb9b06d4631505d37c8383.png) |        | 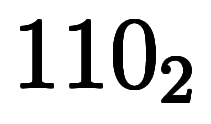 | 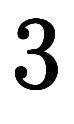 |
 | 8 | ![[1, 1, 1, 1] $$ [1, 1, 1, 1] $$](./eq/eq-ni-bdee9a930a273f9def272529f48c9ba9.png) |        | 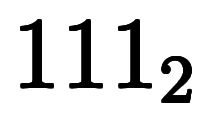 | 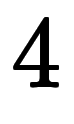 |
2進数であるため、1桁増やすことは、末尾に「 」または「
」または「 」を付ける規則で表現できる。
」を付ける規則で表現できる。
この規則を利用すると、 桁の分割から
桁の分割から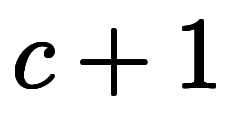 桁の分割を過不足無く作り出せる。
桁の分割を過不足無く作り出せる。
表3: 漸化式的な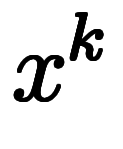 | ||||||||
|---|---|---|---|---|---|---|---|---|
 |  | |||||||
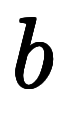 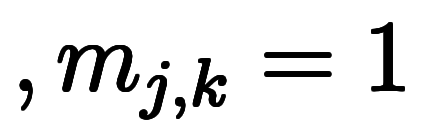 | ||||||||
 |    |     | ||||||
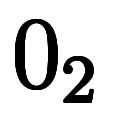 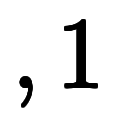 | 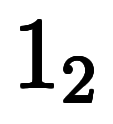 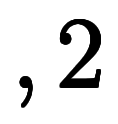 | |||||||
 |      |      |       |      | ||||
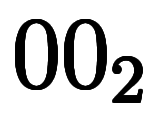  | 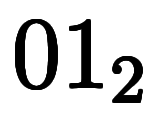 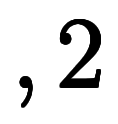 | 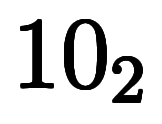 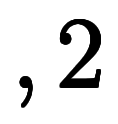 | 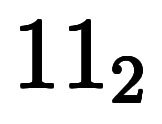 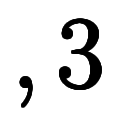 | |||||
 |        |        |        |         |         |        |      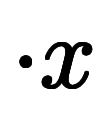 |        |
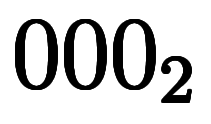  | 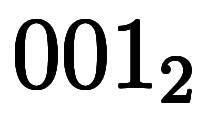  | 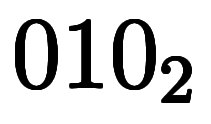 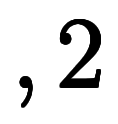 | 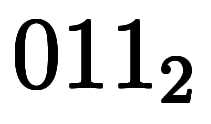 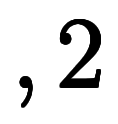 | 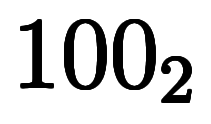  | 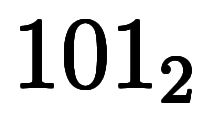  | 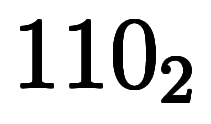 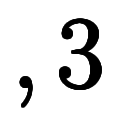 |   | |
 |  | |||||||
これから、 のとき、
のとき、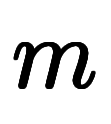 分割される
分割される![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png) について考え、漸化式を作る。
について考え、漸化式を作る。
厳密にするため、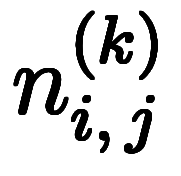 のように右上添字で異なる
のように右上添字で異なる を作る
を作る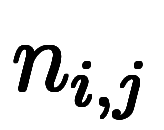 を区別する。
を区別する。
![[n_{i,\,j}^{(k)}] $$ [n_{i,\,j}^{(k)}] $$](./eq/eq-ni-e625adebff610dac571913cb93161de1.png)

![[n_1, n_2, \cdots, n_m] $$ [n_1, n_2, \cdots, n_m] $$](./eq/eq-ni-c0378bde6e194811b7015897b5eb0863.png) とおくと、
とおくと、 の項を作る規則を次のように表現できる:
の項を作る規則を次のように表現できる:
|
|



「係数の抽出」の節で得られた結果より、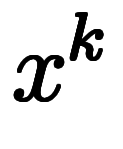 の係数は
の係数は

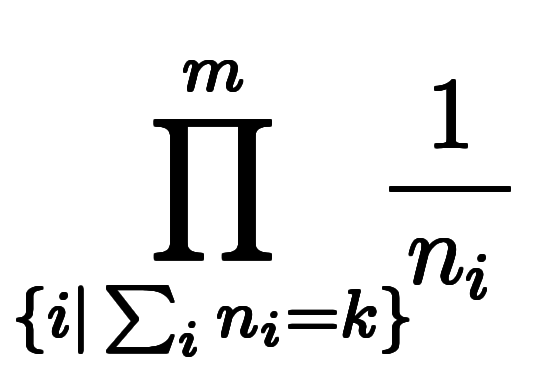 。
。
「冪の漸化式」の節で得られた結果より、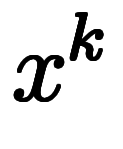 となる項は全部で
となる項は全部で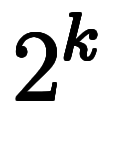 個現れる。
個現れる。
このため、総和記号 の上限は実際
の上限は実際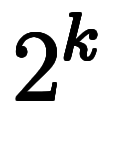 で止まり*1、
で止まり*1、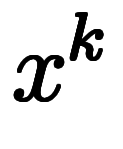 の係数は
の係数は

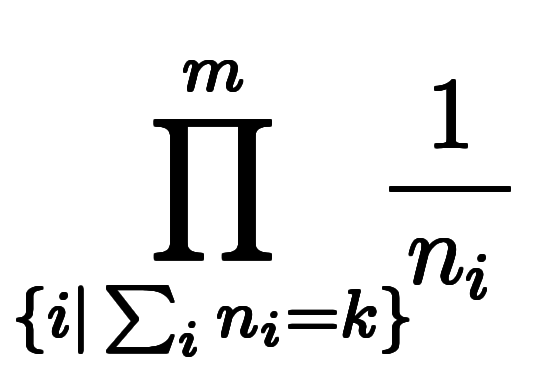 になる。
になる。
さらに、総和記号 を落とすと、
を落とすと、![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png)

![[n_1, n_2, \cdots, n_m] $$ [n_1, n_2, \cdots, n_m] $$](./eq/eq-ni-c0378bde6e194811b7015897b5eb0863.png) のように分割される
のように分割される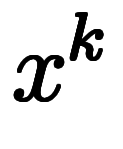 の係数
の係数![a_{[n_i]} $$ a_{[n_i]} $$](./eq/eq-ni-bbf05caa73b5019bba05d5c9ca0df9aa.png) が得られる:
が得られる:
|
同様に、![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png) に対応する
に対応する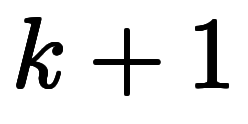 次の係数は以下のようになる。
次の係数は以下のようになる。
|
|
共に分母分子を調節して、![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png) を作り出すと係数の漸近式になる:
を作り出すと係数の漸近式になる:
| |
|
|
|
|

















