![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
指数対数の合成関数の無限級数展開 のバックアップ(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
指数対数の合成関数の無限級数展開 のバックアップ(No.3) |
設問 |
|
|
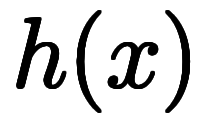

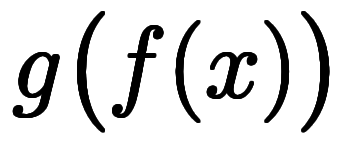 とすると、指数計算により
とすると、指数計算により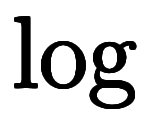 と
と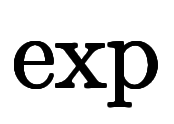 が打消し、簡単な式になる:
が打消し、簡単な式になる:
|
一方で、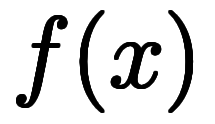 と
と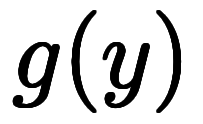 を級数展開しても
を級数展開しても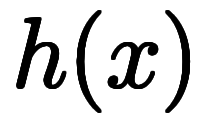 の級数の形で求まるはず:
の級数の形で求まるはず:
|
|
よって: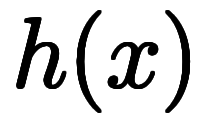

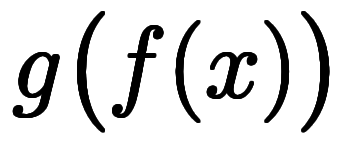


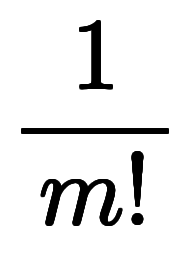
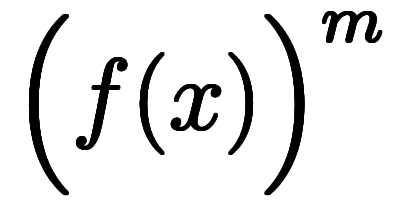



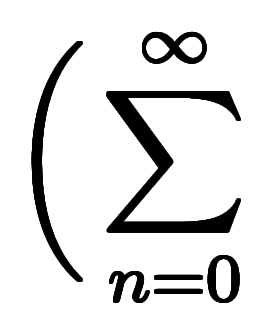
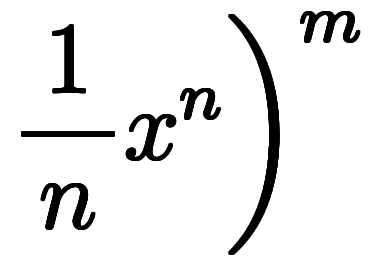
一方で、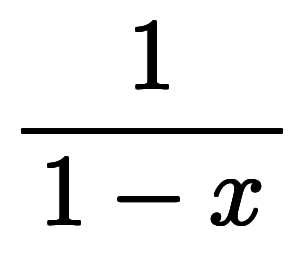


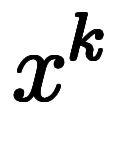 *2のため、
*2のため、

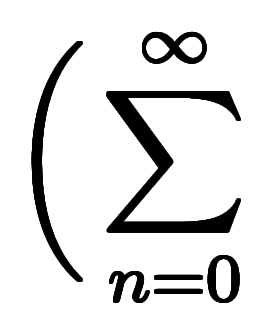
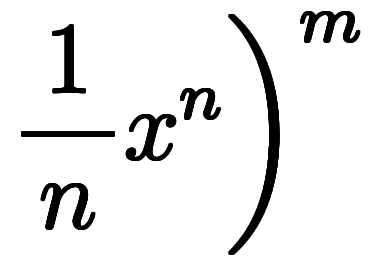


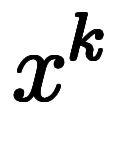 が成り立つ。
が成り立つ。
そこで係数比較すると、任意の

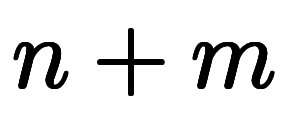 について
について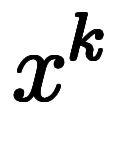 の係数は1でなければならない結論に至る。
の係数は1でなければならない結論に至る。
が、真面目に展開しても無限級数の入子であるため、簡単には導けない。





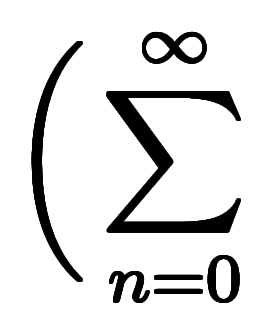
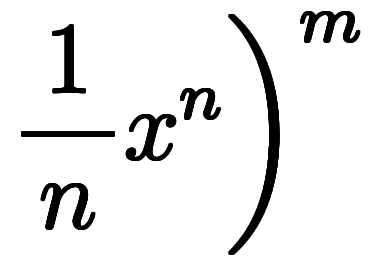 について、
について、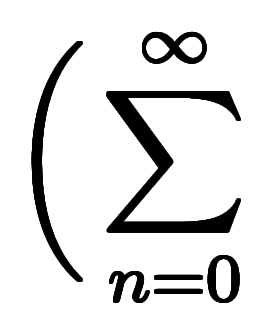
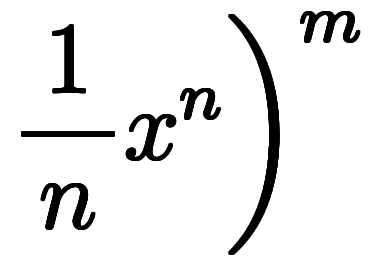 の部分は
の部分は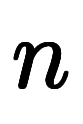 次多項式の
次多項式の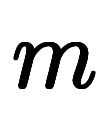 乗展開を意味する。
乗展開を意味する。
このため、直接多項式展開の記述
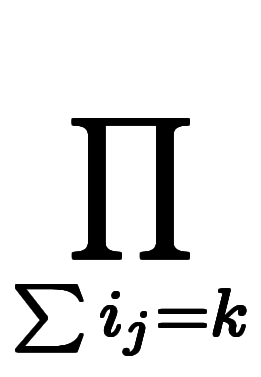
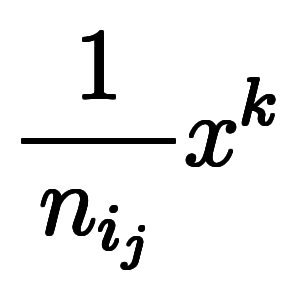 に置き換えできる。
に置き換えできる。
したがって、

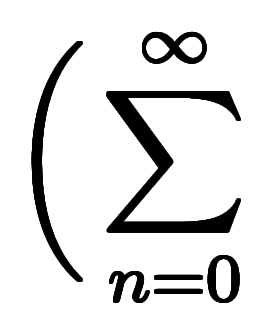
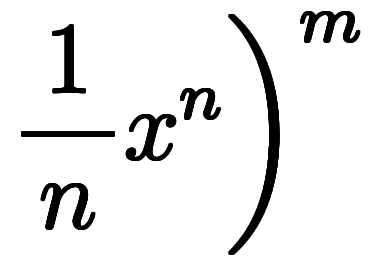





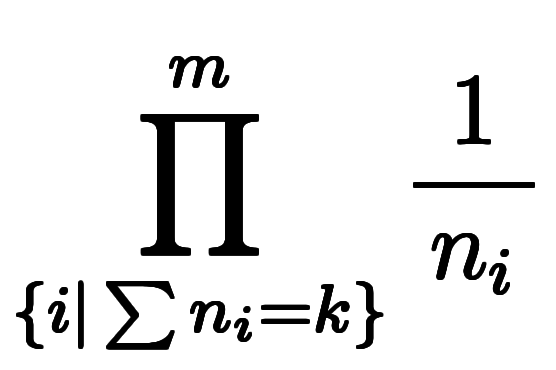

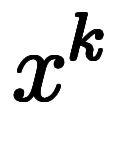






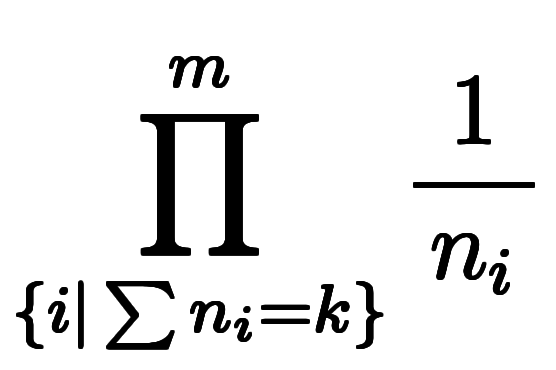

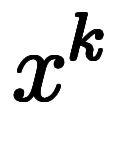
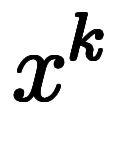 の係数を抜き出すと、任意の
の係数を抜き出すと、任意の について以下の式が成り立つ。
について以下の式が成り立つ。
|
ここで、総乗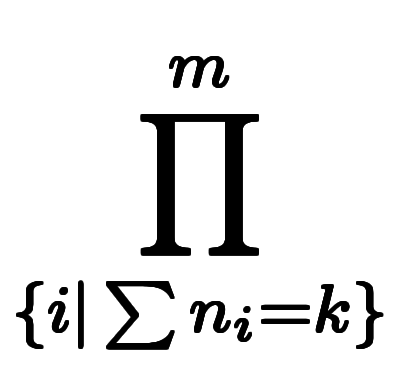 の条件式は、自然数範囲で
の条件式は、自然数範囲で について多項の加数分解を行い、結果の加数の総乗を取る意味である。
について多項の加数分解を行い、結果の加数の総乗を取る意味である。
また、上限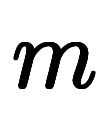 は、加数分解結果より
は、加数分解結果より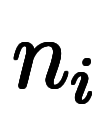 項数が決まり、
項数が決まり、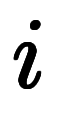 の上限である
の上限である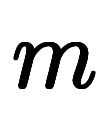 が逆に制限されることを意味する。
が逆に制限されることを意味する。
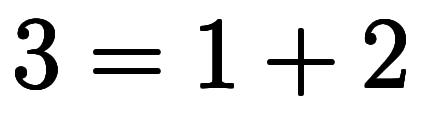
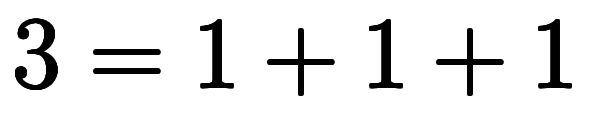
例えば、具体的に の場合、
の場合、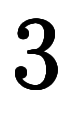 を以下のように加数分解を行い、
を以下のように加数分解を行い、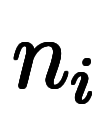 と
と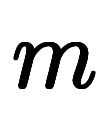 が決まる:
が決まる:
| 加数分解 | ![[n_i] $$ [n_i] $$](./eq/eq-ni-c4509dece8c8dd9bf1fc88ae8c4b4b50.png) | 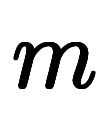 |
|---|---|---|
 | ![[3] $$ [3] $$](./eq/eq-ni-50a97a3b5b3348fbc68b43b203994c07.png) |  |
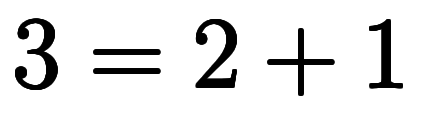 | ![[2, 1] $$ [2, 1] $$](./eq/eq-ni-6f1753ca2b432d81e0d05bf782b0c3da.png) | 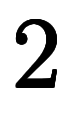 |
 | ![[1, 2] $$ [1, 2] $$](./eq/eq-ni-2f4e1906214533bb447e699d1e3c641e.png) | 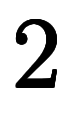 |
 | ![[1, 1, 1] $$ [1, 1, 1] $$](./eq/eq-ni-6c8b1ef6d34ffe22ff722f5e384139ee.png) | 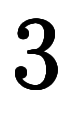 |