![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
単位ベクトル のバックアップの現在との差分(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
単位ベクトル のバックアップの現在との差分(No.3) |
|
  ![\iro[ao]{|\:a|} $$ \iro[ao]{|\:a|} $$](./eq/eq-ni-aaaf42a9e1f3473b26002cdd16c6d118.png) ![\iro[md]{\ffd{\:a}{|\:a|}} $$ \iro[md]{\ffd{\:a}{|\:a|}} $$](./eq/eq-ni-b1b9ae7a7f5ea86552d0a4aee4440694.png) (ただし、 (ただし、![\iro[md]{|\:a|} $$ \iro[md]{|\:a|} $$](./eq/eq-ni-43887727d84f3e77e01ad306f5658933.png)   ) ) |
 という表記法がある*1。しかし、この表記法は
という表記法がある*1。しかし、この表記法は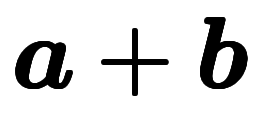 や
や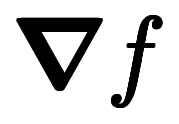 のような式には使えない。
のような式には使えない。 や
や のような式の単位ベクトルには使い難い。そこで、凌宮数学では、単位ベクトルを「
のような式の単位ベクトルには使い難い。そこで、凌宮数学では、単位ベクトルを「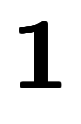 」と表記する。大きさが「1」だから「1」と書きたいだけだが、これより式が直感的に読みやすくなる。また、表記の自由度を高めるため、作用対象との関係を以下の2通りとする。
」と表記する。大きさが「1」だから「1」と書きたいだけだが、これより式が直感的に読みやすくなる。また、表記の自由度を高めるため、作用対象との関係を以下の2通りとする。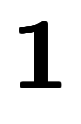 」と表記する。
」と表記する。 のベクトルであるため、太字の1を選んだ。
のベクトルであるため、太字の1を選んだ。 に対する単位ベクトルは
に対する単位ベクトルは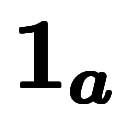 と表記する。これは主に
と表記する。これは主に の表記に対応し、全体を一つの記号として扱うときに用いる省略記法である。
の表記に対応し、全体を一つの記号として扱うときに用いる省略記法である。 に対する単位ベクトルは
に対する単位ベクトルは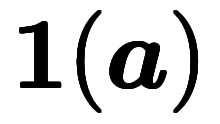 と表記する。これより、式に対して
と表記する。これより、式に対して や
や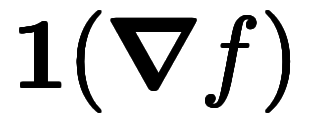 のように表記できる。
のように表記できる。 に対し、以下2つの表記を定義する。
に対し、以下2つの表記を定義する。 : 単位ベクトル自体を表す意味合いが強い略記法。
: 単位ベクトル自体を表す意味合いが強い略記法。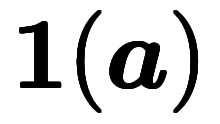 : 単位ベクトルを求める演算を表す意味外が強い表記法。
: 単位ベクトルを求める演算を表す意味外が強い表記法。


 や
や 。
。 と同じ向きの方向ベクトルを
と同じ向きの方向ベクトルを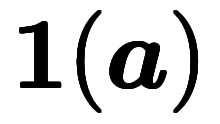

 と定義できる。
と定義できる。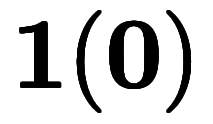

 と定義しておくと、
と定義しておくと、  ![\iro[ao]{|\:a|} $$ \iro[ao]{|\:a|} $$](./eq/eq-ni-aaaf42a9e1f3473b26002cdd16c6d118.png) ![\iro[md]{\:1_{\:a}} $$ \iro[md]{\:1_{\:a}} $$](./eq/eq-ni-e36ab77c22469b0ee3e27cffc4235935.png) |



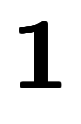 」は役になったことになる。「1」っぽく書いて初めて気づくのであれば、この「
」は役になったことになる。「1」っぽく書いて初めて気づくのであれば、この「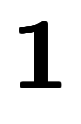 」は役に立ったことになる。
」は役に立ったことになる。



 、
、 、
、 座標系の単位ベクトルは、添字表記を用いて
座標系の単位ベクトルは、添字表記を用いて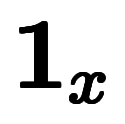 、
、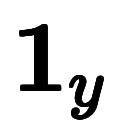 、
、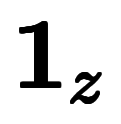 と表記する。
と表記する。
任意のベクトル に対し、単位方向ベクトルを
に対し、単位方向ベクトルを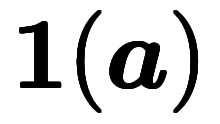 または
または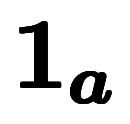 と表記する。
と表記する。



 を基底とする1次元ベクトルと見なすことができる。このため、任意のスカラー
を基底とする1次元ベクトルと見なすことができる。このため、任意のスカラー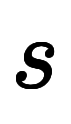 の単位ベクトルを
の単位ベクトルを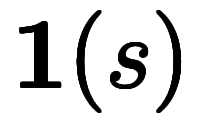

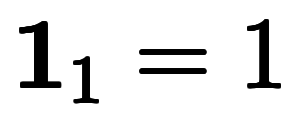 と表記できる。
と表記できる。



 を基底とする1次元ベクトルと見なせる。このため、任意のスカラー
を基底とする1次元ベクトルと見なせる。このため、任意のスカラー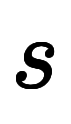 の単位ベクトルを
の単位ベクトルを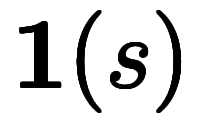 と表記できる。
と表記できる。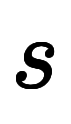 は正の数
は正の数 なら、
なら、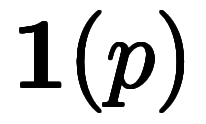

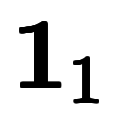

 となる。
となる。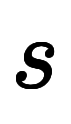 は負の数
は負の数 なら、
なら、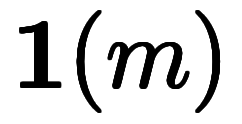

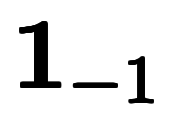

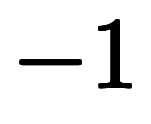 となる。
となる。 もまた立派な単位ベクトルである。また、この結果から、実数では
もまた立派な単位ベクトルである。また、この結果から、実数では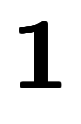 で符号を表せるのが分かる
で符号を表せるのが分かる



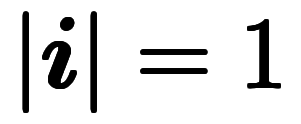 のため正規である。このため、
のため正規である。このため、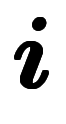 を
を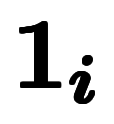 と表記できる。複素数では
と表記できる。複素数では と虚数単位
と虚数単位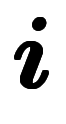 を基底とするベクトルと見なせる。このため、任意の複素数
を基底とするベクトルと見なせる。このため、任意の複素数 に対し、
に対し、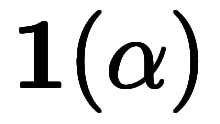

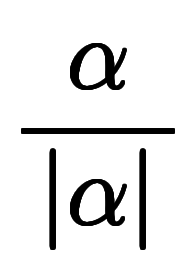 と定義できる。この定義に従えば、
と定義できる。この定義に従えば、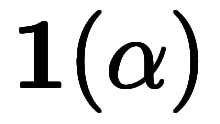 は虚数平面上の単位円上の点となる。値としては、
は虚数平面上の単位円上の点となる。値としては、 の極形式を
の極形式を とすると、
とすると、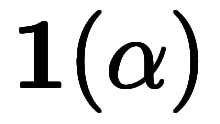



 となる。特殊な単位ベクトルとして、実数にあった
となる。特殊な単位ベクトルとして、実数にあった と
と の他、虚数単位
の他、虚数単位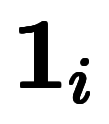

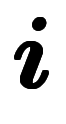 とその逆である
とその逆である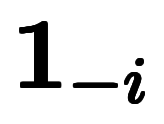

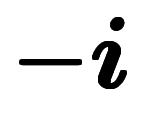 が挙げられる。
が挙げられる。




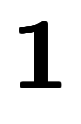 に一致する。実数
に一致する。実数 に対し、符号関数は
に対し、符号関数は


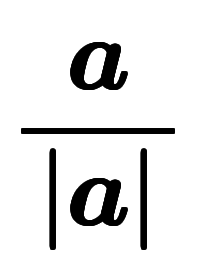
#spanend &spanadd; \Bigg\{&spanend; &spanadd; \begin{array}{rcc}&spanend; &spanadd; 1 & : & a > 0&spanend; &spanadd; \\ 0 & : & a = 0&spanend; &spanadd; \\ -1 & : & a < 0&spanend; &spanadd; \end{array}&spanend; #spanadd として定義される。また、複素数に拡張した場合、


#spanend &spanadd; \bigg\{&spanend; &spanadd; \begin{array}{ccc}&spanend; &spanadd; \ffd{\alpha}{|\alpha|} & : & \alpha \neq 0&spanend; &spanadd; \\ 0 & : & \alpha = 0 \ffdstrut&spanend; &spanadd; \end{array}&spanend; #spanadd となる。この複素数の定義は実数の定義を含む。ここで、複素数の定義は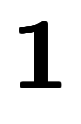 の定義と一致しているのが分かる。したがって、複素数に対し、
の定義と一致しているのが分かる。したがって、複素数に対し、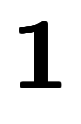 と
と は等価である。
は等価である。