![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分演算子 のバックアップ(No.4) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数1階線形常微分演算子 のバックアップ(No.4) |
【編集中】凌宮読取術: |
|
定数係数の高階線形常微分方程式を解くため、
微分演算子

 による演算子法が工学で多用される*1:
による演算子法が工学で多用される*1:
|
右辺を比較すれば、次の関係式が出てくる。
|
一般的な演算子法でも、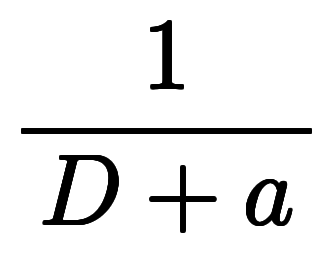 は暗記対象になるが、
は暗記対象になるが、
しかし、この左辺と右辺の対応は直観的ではなく、暗記は難しい。
これに対し、凌宮数学では、線形偏微分演算子 を更に分解し、
を更に分解し、
直感的に考えやすいように単純な演算子を用いて、暗記な暗記に置き換える。



 の逆演算子
の逆演算子 


一般に、微分


 に対し、不定積分
に対し、不定積分



 が定義される。
が定義される。
このため、微分演算 の逆演算
の逆演算 は不定積分
は不定積分 〜
〜 となる。
となる。
 の分解表記
の分解表記 


定数係数の1階線形常微分方程式とその解の公式の積分を で書き換えると:
で書き換えると:
|
このため、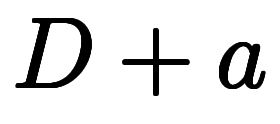 の逆演算子である
の逆演算子である は形式的に次のように分解できる:
は形式的に次のように分解できる:
|
 と書いている箇所に作用対象が入る。
と書いている箇所に作用対象が入る。
 と
と の作用対象である
の作用対象である の両方が
の両方が の積分対象に入るのがポイントである。
の積分対象に入るのがポイントである。
しかし、 を抜いて、単に
を抜いて、単に
 と書くと、
と書くと、 だけの積分に化けてしまう。
だけの積分に化けてしまう。
表記の曖昧さを無くすため、 も演算子にする必要がある。
も演算子にする必要がある。






凌宮数学では指数変換演算子を以下のように定義する。
|
演算子であるため、必ず何かに作用し、
 だけで
だけで
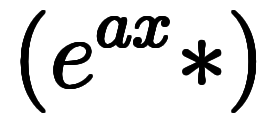 を意味する。
を意味する。
すると、 は
は と
と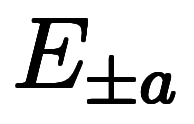 の演算子チェーンとして記述できる:
の演算子チェーンとして記述できる:
|
さらに、 は
は の掛算であるため、逆演算子
の掛算であるため、逆演算子 は
は の逆数の掛算となる:
の逆数の掛算となる:
|
これを利用すれば、 は
は と
と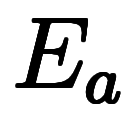 だけの演算子チェーンとして記述できる:
だけの演算子チェーンとして記述できる:
|
意味は、 で変換してから、積分して、逆変換を掛ける、と読める。
で変換してから、積分して、逆変換を掛ける、と読める。
 の分解表記
の分解表記 




 の逆演算を取ると、
の逆演算を取ると、 が得られる:
が得られる:
| |
= | 演算子チェーンの逆演算は、各演算子の逆演算を逆順に並び |
= | 逆演算の逆演算は正演算 |
ポイントは が正演算に戻るだけで、
が正演算に戻るだけで、 と
と に関しては変わりが無い。
に関しては変わりが無い。
|
意味は、 で指数変換してから、微分し、逆変換を掛ける、と読める。
で指数変換してから、微分し、逆変換を掛ける、と読める。



未知関数 と既知関数
と既知関数 に着目すると、原方程式と解の公式はそれぞれ次のように捉えられる:
に着目すると、原方程式と解の公式はそれぞれ次のように捉えられる:
 に対し微分を含む操作を施すと既知関数
に対し微分を含む操作を施すと既知関数 が得られる
が得られる に対し微分を含む操作を施すと未知関数
に対し微分を含む操作を施すと未知関数 が得られる
が得られるそうすると、上記解答は次のように見える:
| |
| 原方程式 |
⇔ | 両辺に積分因子 |
⇔ | 積の微分に嵌める(不定積分を実行) |
⇔ | 1つの微分に纏める(部分積分を実行) |
⇔ | 積分する |
⇔ | 両辺に |
上記の解き方では、 と
と では単純な微分・積分の関係にならないため、
では単純な微分・積分の関係にならないため、
一旦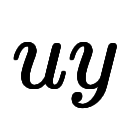

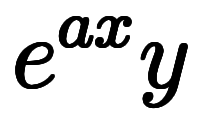 と
と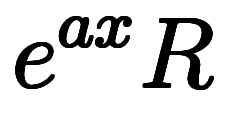 に変換してから、単純な微分を単純な積分に直している。
に変換してから、単純な微分を単純な積分に直している。
そういう意味で、解答例の最初と最後だけに着目すると、 と
と に関する一対の複雑な微分と積分にも見える:
に関する一対の複雑な微分と積分にも見える:




 が
が から
から への複雑な微分
への複雑な微分

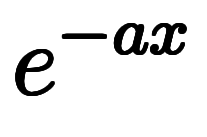



 は
は から
から への複雑な積分
への複雑な積分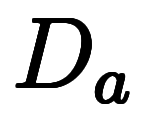 を
を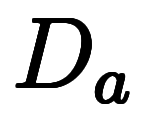






 と定義し、
と定義し、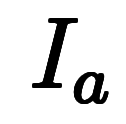 を
を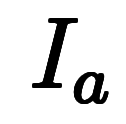






 と定義すると、
と定義すると、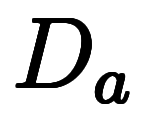
![\iro[gy]y $$ \iro[gy]y $$](./eq/eq-ni-48d32a2569f09f042196c7ad3e4b5898.png)

![\iro[gy]R $$ \iro[gy]R $$](./eq/eq-ni-2d930a54fd3cb219703755c888a54f90.png) ⇔
⇔ ![\iro[gy]y $$ \iro[gy]y $$](./eq/eq-ni-48d32a2569f09f042196c7ad3e4b5898.png)

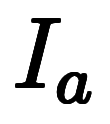
![\iro[gy]R $$ \iro[gy]R $$](./eq/eq-ni-2d930a54fd3cb219703755c888a54f90.png)
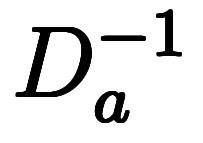

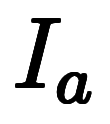





 と置きながら
と置きながら


 の解になるのが非論理的な面がある
の解になるのが非論理的な面がある