![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分/偏微分と常微分の違い のバックアップ(No.6) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分/偏微分と常微分の違い のバックアップ(No.6) |
偏微分と常微分の違いは、定義式から「固定する変数の有無」というのがお墨付きの答えである。
ここで言う「固定する変数」とは偏微分の方に現れる赤い「 しかし、その違いは関数
このため、偏微分と常微分の違いを説明するには、 偏微分と常微分が異なる |
|
もし

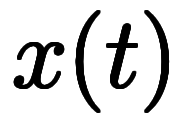 、
、

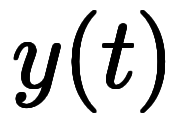 という関係であれば、
という関係であれば、 を
を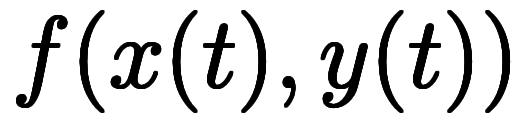 として
として の関数に書き換えられる。このため、
の関数に書き換えられる。このため、 による
による の常微分が存在する:
の常微分が存在する:
ここまでは多くのテキストで述べられている。これの を
を に直せば、
に直せば、![\iro[ak]{\ppd{f}{x}} $$ \iro[ak]{\ppd{f}{x}} $$](./eq/eq-ni-9e129251ddbbe5ac2b9870f5586ff4c7.png) と
と![\iro[ao]{\ddd{f}{x}} $$ \iro[ao]{\ddd{f}{x}} $$](./eq/eq-ni-28748a8b3bf61554b0b035e62d970bd3.png) が出揃う。
が出揃う。
|



これを利用し、![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) と
と![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) を揃えるには、
を揃えるには、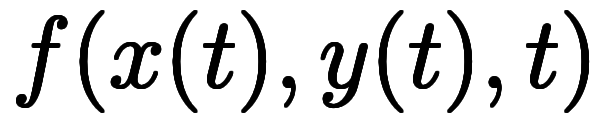 *2のような
*2のような を含む関数を考える必要がある。
を含む関数を考える必要がある。
まず、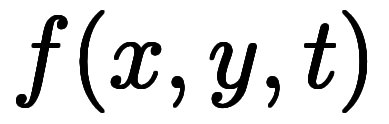 から、
から、 の全微分は次のよう書ける。
の全微分は次のよう書ける。
|
次ぎに、

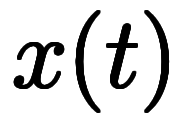 、
、

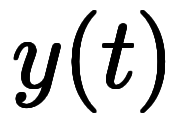 を代入すれば、
を代入すれば、 は
は の関数に化ける*3。このため、常微分が存在し、式の両辺を
の関数に化ける*3。このため、常微分が存在し、式の両辺を で割ることで
で割ることで![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) を作り出せる。
を作り出せる。
|
 が
が と
と と
と の影響を受ける限り、どの項も消えず、「偏微分と常微分は違う」という結論に至る。
の影響を受ける限り、どの項も消えず、「偏微分と常微分は違う」という結論に至る。
|
 は、
は、 と
と に関する2変数関数でありながら、
に関する2変数関数でありながら、 に関する1変数関数にもなっている。変数の数が絶対的でなくなっている点に注意。
に関する1変数関数にもなっている。変数の数が絶対的でなくなっている点に注意。


偏微分と常微分の違いは前節の通りである。しかし、これは一見良さそうだが、式の意味を読み取ろうとすると偏微分の矛盾が見えてくる*4。
例えば、 が
が に関する1変数関数に化けられるなら、冒頭で述べたように1変数関数を多変数関数の特例と見なせて、常微分と等価な青い偏微分が存在することになる。
に関する1変数関数に化けられるなら、冒頭で述べたように1変数関数を多変数関数の特例と見なせて、常微分と等価な青い偏微分が存在することになる。
|
これに、前節で得た![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png)

![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) を合わせると、次の矛盾が得られる。
を合わせると、次の矛盾が得られる。
|




条件を少し変えて、中途半端な について考えてみよう。「
について考えてみよう。「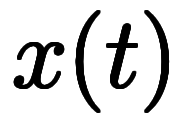 と書いていたが、実は
と書いていたが、実は に
に が含まれて無く、
が含まれて無く、 だけに
だけに が含まれていた」という話。
が含まれていた」という話。
すると、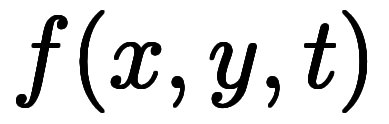 であることに変わらないため、次の全微分も変わらず成立する。
であることに変わらないため、次の全微分も変わらず成立する。
|
しかし、今度は に
に

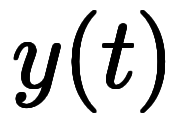 を代入しても
を代入しても だけの関数にはならない。代わりに
だけの関数にはならない。代わりに は
は と
と に関する2変数関数になるため、次の全微分が成り立つ。
に関する2変数関数になるため、次の全微分が成り立つ。
|
問題は、この紫の偏微分は赤い偏微分と別物で、両式を比較すると以下の関係が得られる。
|
それも、 が
が の影響を、
の影響を、 が
が の影響を受ける限り、どの項も消えず
の影響を受ける限り、どの項も消えず![\iro[mr]{\ppd{f}{t}} $$ \iro[mr]{\ppd{f}{t}} $$](./eq/eq-ni-907eadbab741099886ff2ddc100fa0fc.png)

![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) の関係を持つ。
の関係を持つ。
同様に代入の加減をすれば、赤、紫、青以外にも、色んな偏微分を作ることができる。



多くの場合、赤い偏微分と青い偏微分しか使われないため、![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) と
と![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) で区別できる。ただ、他の偏微分に気づいた人から混乱が始まる。
で区別できる。ただ、他の偏微分に気づいた人から混乱が始まる。
この混乱を無くすには、色んな偏微分を厳密に書き分け、正しく整理する必要がある。そうすれば、自ずと偏微分と常微分を一貫した表記で書けるようになる。また、書き表せないものを書けるようになったとき、新しい発想ができるようになるかもしれない。