![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分と常微分の違い のバックアップ(No.14) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分と常微分の違い のバックアップ(No.14) |
偏微分と常微分の違いを問われて、多くの人は「固定する変数の有無」と答える。 これは定義式を眺めば頷ける。
ここで言う「固定する変数」とは偏微分の方に現れる赤い「 しかし、「その違いは関数 実際、1変数関数は2変数関数の特殊例と見なすことができ、その場合の偏微分は常微分と一致する。
この疑問に答えるには、同一関数に対し 偏微分と常微分の違い準備として、2変数関数
ここで、 ここまでは多くのテキストで述べられている。これを利用し、 まず、
次ぎに、
しかし、これは一見良さそうに見えるが、式の意味を読み取ろうとすると偏微分の限界が見えてくる*4。 例えば、
ここから、 *1
偏微分を駆け足で学ぶ人には、恐らくこれが同一関数に対して
 と と が並存する最初の式で、混乱が始まりである。 が並存する最初の式で、混乱が始まりである。*2 この関数は、EMANの物理学/解析力学/全微分で偏微分と常微分の違いを説明するのに用いられている。ページ自体は全微分の話である。偏微分と常微分の違いはその一番最後の節で述べられている。 *3 この時点で、  は、 は、 と と に関する2変数関数でありながら、 に関する2変数関数でありながら、 に関する1変数関数にもなっている。変数の数が絶対的でなくなっている点に注意。 に関する1変数関数にもなっている。変数の数が絶対的でなくなっている点に注意。*4 注意:問題は偏微分の方である。EMANの物理の説明自体は正しい。その説明は私が納得できた唯一の説明でもある。むしろ、偏微分の欠点を上手く隠した分かりやすい説明である。 中途半端な |
|
しかし、今度は

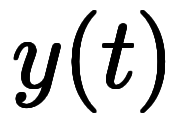 を代入しても
を代入しても だけの関数にはならない。代わりに
だけの関数にはならない。代わりに は
は と
と に関する2変数関数になるため、次の全微分が成り立つ。
に関する2変数関数になるため、次の全微分が成り立つ。
|
問題は、この紫の偏微分は赤い偏微分と別物で、両式を比較すると以下の関係が得られる。
|
それも、 が
が の影響を、
の影響を、 が
が の影響を受ける限り、どの項も消えず
の影響を受ける限り、どの項も消えず![\iro[mr]{\ppd{f}{t}} $$ \iro[mr]{\ppd{f}{t}} $$](./eq/eq-ni-907eadbab741099886ff2ddc100fa0fc.png)

![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) の関係を持つ。
の関係を持つ。
以下では、

![\iro[md]{1x} $$ \iro[md]{1x} $$](./eq/eq-ni-7f152d84d7df2ed88a6bed84e68c9704.png)

![\iro[ao]{2y} $$ \iro[ao]{2y} $$](./eq/eq-ni-e20a6979c935857e8ed753e95c144a37.png)

![\iro[ak]{3t} $$ \iro[ak]{3t} $$](./eq/eq-ni-1884eb78aab12b6b85dde699ef562340.png) を用いて、これまでの問題を直観的に纏める。
を用いて、これまでの問題を直観的に纏める。
まず、 を次のように展開できる。
を次のように展開できる。
|
これに対し、全微分は次のように作れる。
|


![\iro[md]{1x} $$ \iro[md]{1x} $$](./eq/eq-ni-7f152d84d7df2ed88a6bed84e68c9704.png)

![\iro[ao]{2y} $$ \iro[ao]{2y} $$](./eq/eq-ni-e20a6979c935857e8ed753e95c144a37.png)

![\iro[ak]{3t} $$ \iro[ak]{3t} $$](./eq/eq-ni-1884eb78aab12b6b85dde699ef562340.png) から、赤い偏微分
から、赤い偏微分![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png)

![\iro[ak]{3} $$ \iro[ak]{3} $$](./eq/eq-ni-0d2932b6e42863b6345e67bb27901bb4.png) が得られる。
が得られる。
ポイントは、![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) を「赤い
を「赤い![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) の個数」として読めることである。
の個数」として読めることである。
同様に、 に
に

 と
と

 を代入すると、
を代入すると、

 を得る。
を得る。
全微分は

![\iro[md]{dt} $$ \iro[md]{dt} $$](./eq/eq-ni-71de70cdce3d687d27433034d74add37.png)

![\iro[md]{dt} $$ \iro[md]{dt} $$](./eq/eq-ni-71de70cdce3d687d27433034d74add37.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) 。
。
常微分![\iro[md]{\ddd{f}{t}} $$ \iro[md]{\ddd{f}{t}} $$](./eq/eq-ni-5ec43bfb81da30364796b6d2fcd4f4cf.png)

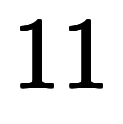 は「緑、青、赤を合わせた
は「緑、青、赤を合わせた を個数」を表す。
を個数」を表す。
対して、赤い偏微分は変わらず、赤い![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) のみを数えた
のみを数えた![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png)

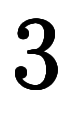 である。
である。
一見良さそうに見えるが、

 を見る限り、
を見る限り、
次ぎに、限界の話では

 のみを代入し、
のみを代入し、



 作った。
作った。
全微分は

![\iro[md]{dx} $$ \iro[md]{dx} $$](./eq/eq-ni-562390122be48ed65e2944b6051cf330.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) 。
。
登場した青い偏微分は![\iro[ao]{dy} $$ \iro[ao]{dy} $$](./eq/eq-ni-c594c98f7b472814d977dfd12fd44681.png) と
と![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) の分を数えた
の分を数えた![\iro[ao]{\ppd{f}{t}} $$ \iro[ao]{\ppd{f}{t}} $$](./eq/eq-ni-bd06a061e32f7d1959c5b7d8d7cb2d55.png)

 である。
である。
対して、赤い偏微分は![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) の分のみを数えた
の分のみを数えた![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png)

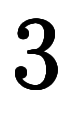 である。
である。
さらに、際どく「1つの だけを
だけを に変換」して、
に変換」して、





 を作ることもできる。この場合、全微分は
を作ることもできる。この場合、全微分は

![\iro[md]{dx} $$ \iro[md]{dx} $$](./eq/eq-ni-562390122be48ed65e2944b6051cf330.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png)

![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) 、
、
1つの![\iro[ao]{dy} $$ \iro[ao]{dy} $$](./eq/eq-ni-c594c98f7b472814d977dfd12fd44681.png) と
と![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) を数えた紫の偏微分
を数えた紫の偏微分![\iro[mr]{\ppd{f}{t}} $$ \iro[mr]{\ppd{f}{t}} $$](./eq/eq-ni-907eadbab741099886ff2ddc100fa0fc.png)

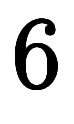 と、
と、
赤い![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) のみを数えた赤い
のみを数えた赤い![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png)

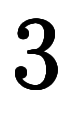 が考えられる。
が考えられる。
以上を図に纏めると次のようになる:
以上から次の結論が得られる:
同じ関数に対し、常微分と偏微分が同時に存在して異なる場合は、偏微分が複数の意味を持って破綻する。 |
このように、 、
、 、
、 の間に関係式を持てば、
の間に関係式を持てば、 を変えずに
を変えずに の数を任意に増減できてしまう。その結果、
の数を任意に増減できてしまう。その結果、 は何個の
は何個の を数えても良く、任意の値を取れることになる。
を数えても良く、任意の値を取れることになる。
1変数関数が多変数関数の特殊例と見なせば、偏微分![\iro[md]{\ppd{f}{t}} $$ \iro[md]{\ppd{f}{t}} $$](./eq/eq-ni-b34e25c863643312177565e3181efe59.png)

 も同じ意味で成り立つ。
も同じ意味で成り立つ。
「

 」と書かれる以上、どの
」と書かれる以上、どの が何色か分からなくなる。
が何色か分からなくなる。
このため、赤い![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) だけを数えたくても無理である。
だけを数えたくても無理である。
以上から、同じ関数の常微分と偏微分が異なる値を表す場合はあるが、その場合に次のことも言える:
 が複数の意味を持ってしまう。
が複数の意味を持ってしまう。 は
は の1例に見える。
の1例に見える。