![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分と常微分の違い のバックアップの現在との差分(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分と常微分の違い のバックアップの現在との差分(No.3) |
|
偏微分と常微分の違いを問われて、多くの人は「固定する変数の有無」と答える。定義式を眺めば頷ける。偏微分と常微分の違いは、定義式から「固定する変数の有無」というのがお墨付きの答えである。
![\iro[ak]{, y} $$ \iro[ak]{, y} $$](./eq/eq-ni-6537dabaa10445ae34895d651b9b5002.png) 」の部分である。ここで言う「固定する変数」とは偏微分の方に現れる赤い「 」の部分である。ここで言う「固定する変数」とは偏微分の方に現れる赤い「![\iro[ak]{, y} $$ \iro[ak]{, y} $$](./eq/eq-ni-6537dabaa10445ae34895d651b9b5002.png) 」である。しかし、その違いは関数 」である。しかし、その違いは関数 の違いで、微分操作自体は青い部分と変わらないようにも見える。 の違いで、微分操作自体は青い部分と変わらないようにも見える。実際、1変数関数は2変数関数の特殊例と見なすことができ、その偏微分は常微分に一致する。 しかし、その違いは「関数 の違いで、微分操作自体は青い部分のまま変わらない」ようにも見える。実際、1変数関数は2変数関数の特殊例と見なすことができ、その場合の偏微分は常微分と一致する。 の違いで、微分操作自体は青い部分のまま変わらない」ようにも見える。実際、1変数関数は2変数関数の特殊例と見なすことができ、その場合の偏微分は常微分と一致する。
   を示す必要がある。 を示す必要がある。その答えは「EMANの物理学/解析力学/全微分/偏微分と常微分の違い*1」でやっと見つかった。 このため、偏微分と常微分の違いを説明するには、同一の多変数関数に対し![\iro[ak]{\ppd{f}{x}} $$ \iro[ak]{\ppd{f}{x}} $$](./eq/eq-ni-9e129251ddbbe5ac2b9870f5586ff4c7.png)  ![\iro[ao]{\ddd{f}{x}} $$ \iro[ao]{\ddd{f}{x}} $$](./eq/eq-ni-28748a8b3bf61554b0b035e62d970bd3.png) を示す必要がある。 を示す必要がある。偏微分と常微分の違いまず、準備として、2変数関数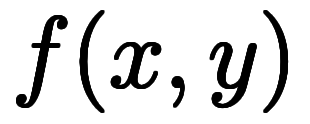 について、次の全微分 について、次の全微分 が次のように定義される。準備として、2変数関数 が次のように定義される。準備として、2変数関数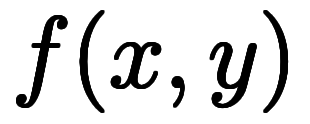 について、次のように定義される全微分 について、次のように定義される全微分 について考える。 について考える。
  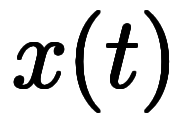 、 、  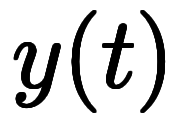 であれば、 であれば、  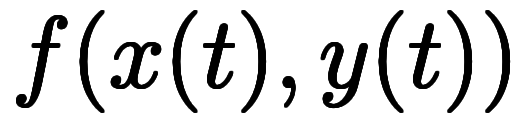 と書けて、 と書けて、 は は の関数ということになる。このため、 の関数ということになる。このため、 による による 常微分が存在し、次のようになる。ここで、 常微分が存在し、次のようになる。ここで、  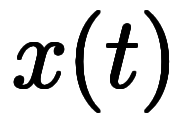 、 、  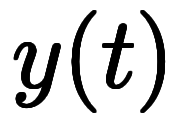 であれば、 であれば、  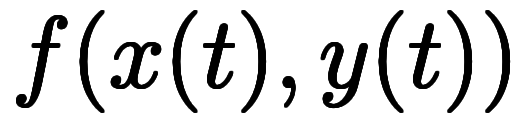 と、 と、 の関数に書き換えられる。このため、 の関数に書き換えられる。このため、 による による の常微分が存在し、次のようになる。 の常微分が存在し、次のようになる。
 に対して に対して と と が並存する初めて式のはず。そして、多くの人はここで混乱するはず。ここまでは多くのテキストで述べられている。しかし、この式では、「分母」が が並存する初めて式のはず。そして、多くの人はここで混乱するはず。ここまでは多くのテキストで述べられている。しかし、この式では、「分母」が 、 、 、 、 と異なっているため、まだ同じ微分とは言えない。これを揃えたのがEMANの物理学で登場する と異なっているため、まだ同じ微分とは言えない。これを揃えたのがEMANの物理学で登場する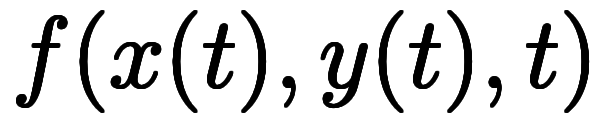 という上手い関数である。これを利用し、 という上手い関数である。これを利用し、![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) と と![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) を揃えるには、 を揃えるには、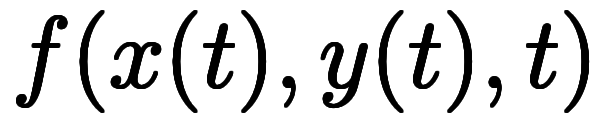 *3のような *3のような を含む関数を考える必要がある。まず、 を含む関数を考える必要がある。まず、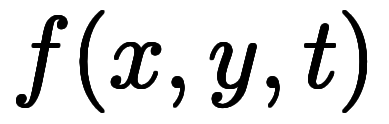 であるため、全微分は次のようになる。まず、 であるため、全微分は次のようになる。まず、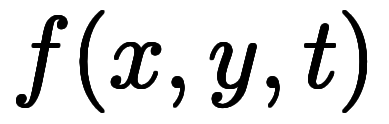 から、 から、 の全微分は次のよう書ける。 の全微分は次のよう書ける。
  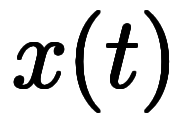 、 、  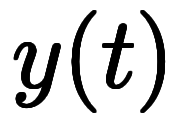 を適応すれば、 を適応すれば、 は は の関数になるため、常微分が次のようになる。次ぎに、 の関数になるため、常微分が次のようになる。次ぎに、  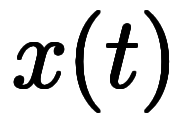 、 、  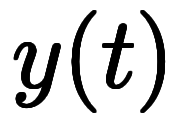 を代入すれば、 を代入すれば、 は は の関数に化ける*4。このため、常微分が存在し、式の両辺を の関数に化ける*4。このため、常微分が存在し、式の両辺を で割ることで で割ることで![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) を作り出せる。 を作り出せる。
   であるため、次のようになる。 であるため、次のようになる。 が が と と と と の影響を受ける限り、どの項も消えず、「偏微分と常微分は違う」という結論に至る。 の影響を受ける限り、どの項も消えず、「偏微分と常微分は違う」という結論に至る。
 が が と と と と の影響を受ける限り、どの項も消えず の影響を受ける限り、どの項も消えず![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png)  ![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) となる。しかし、EMANの物理では話しがココまでだが、この式の意味を読み取ろうとすると、微分表記 となる。しかし、EMANの物理では話しがココまでだが、この式の意味を読み取ろうとすると、微分表記 の限界が見えてくる。 の限界が見えてくる。*2
偏微分を駆け足で学ぶ人には、恐らくこれが同一の関数に対して
 と と が並存する最初の式で、混乱が始まりである。 が並存する最初の式で、混乱が始まりである。*3 この関数は、EMANの物理学/解析力学/全微分で偏微分と常微分の違いを説明するのに用いられている。ページ自体は全微分の話で、偏微分と常微分の違いはその一番最後の節で述べられている。 *4 この時点で、  は、 は、 と と に関する2変数関数でありながら、 に関する2変数関数でありながら、 に関する1変数関数にもなっている。変数の数が絶対的でなくなっている点に注意。 に関する1変数関数にもなっている。変数の数が絶対的でなくなっている点に注意。偏微分と偏微分の違い偏微分と常微分の違いは前節の通りである。しかし、これは一見良さそうだが、式の意味を読み取ろうとすると偏微分の矛盾が見えてくる*5。例えば、 が が に関する1変数関数に化けられるなら、冒頭で述べたように1変数関数を多変数関数の特例と見なせて、常微分と等価な青い偏微分が存在することになる。 に関する1変数関数に化けられるなら、冒頭で述べたように1変数関数を多変数関数の特例と見なせて、常微分と等価な青い偏微分が存在することになる。
![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png)  ![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) を合わせると、次の矛盾が得られる。 を合わせると、次の矛盾が得られる。
|
|
 を代入しても
を代入しても が
が と
と の関数にはなるが、
の関数にはなるが、 だけの関数にはならない。このため、精々次のようにな偏微分しか存在しない。しかし、今度は
だけの関数にはならない。このため、精々次のようにな偏微分しか存在しない。しかし、今度は に
に

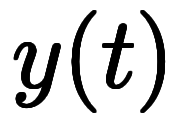 を代入しても
を代入しても だけの関数にはならない。代わりに
だけの関数にはならない。代わりに は
は と
と に関する2変数関数になるため、次の全微分が成り立つ。
に関する2変数関数になるため、次の全微分が成り立つ。 |
 が
が と
と と
と の影響を受ける限り、どの項も消えず
の影響を受ける限り、どの項も消えず![\iro[ao]{\ppd{f}{t}} $$ \iro[ao]{\ppd{f}{t}} $$](./eq/eq-ni-bd06a061e32f7d1959c5b7d8d7cb2d55.png)

![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) となる。問題は、この紫の偏微分は赤い偏微分と別物で、両式を比較すると以下の関係が得られる。
となる。問題は、この紫の偏微分は赤い偏微分と別物で、両式を比較すると以下の関係が得られる。 ;. ![\iro[mr]{\ppd{f}{t}} $$ \iro[mr]{\ppd{f}{t}} $$](./eq/eq-ni-907eadbab741099886ff2ddc100fa0fc.png)     ![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) |
 が
が の影響を、
の影響を、 が
が の影響を受ける限り、どの項も消えず
の影響を受ける限り、どの項も消えず![\iro[mr]{\ppd{f}{t}} $$ \iro[mr]{\ppd{f}{t}} $$](./eq/eq-ni-907eadbab741099886ff2ddc100fa0fc.png)

![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) の関係を持つ。記号衝突である。同様に代入の加減をすれば、赤、紫、青以外にも、色んな偏微分を作ることができる。
の関係を持つ。記号衝突である。同様に代入の加減をすれば、赤、紫、青以外にも、色んな偏微分を作ることができる。
 の限界、その2
の限界、その2 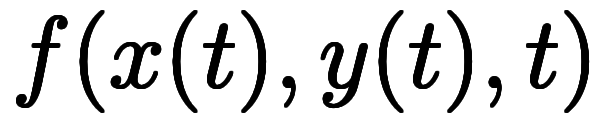 の具体例を考えてみよう。以下では、偏微分の矛盾を
の具体例を考えてみよう。以下では、偏微分の矛盾を

![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)

![\iro[mr]{2y} $$ \iro[mr]{2y} $$](./eq/eq-ni-70701dda354fee189bd626564f8aec53.png)

![\iro[ak]{3t} $$ \iro[ak]{3t} $$](./eq/eq-ni-1884eb78aab12b6b85dde699ef562340.png) という具体例を用いて、直観的に纏めてみる。まず、
という具体例を用いて、直観的に纏めてみる。まず、 に
に

 と
と

 を少しずつ代入すると次の変形が得られる。
を少しずつ代入すると次の変形が得られる。 |  ![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)  ![\iro[mr]{2y} $$ \iro[mr]{2y} $$](./eq/eq-ni-70701dda354fee189bd626564f8aec53.png)  ![\iro[ak]{3t} $$ \iro[ak]{3t} $$](./eq/eq-ni-1884eb78aab12b6b85dde699ef562340.png) | 与式 |
 ![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)  ![\iro[mr]{1y} $$ \iro[mr]{1y} $$](./eq/eq-ni-8e5a0bdbc6ae0340f33135f3f0a2bdb9.png)  ![\iro[pk]{6t} $$ \iro[pk]{6t} $$](./eq/eq-ni-ff6581ba1f6a6f984a72c0cf6beebf9d.png) |    を用いて、1つの を用いて、1つの を を に変換 に変換 | |
 ![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)    ![\iro[mr]{9t} $$ \iro[mr]{9t} $$](./eq/eq-ni-27d7c80343ecb1c1e735b721c2fb7529.png) | もう1つの  も も に変換 に変換 | |
     ![\iro[ao]{11t} $$ \iro[ao]{11t} $$](./eq/eq-ni-d5afd8dfdfec76914aed26944a8959ab.png) |    を用いて、 を用いて、 を を に変換 に変換 |
 のため、
のため、

 は間違いない。それぞれの式から次の偏微分が考えられる:
は間違いない。それぞれの式から次の偏微分が考えられる: |  ![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)  ![\iro[mr]{2y} $$ \iro[mr]{2y} $$](./eq/eq-ni-70701dda354fee189bd626564f8aec53.png)  ![\iro[ak]{3t} $$ \iro[ak]{3t} $$](./eq/eq-ni-1884eb78aab12b6b85dde699ef562340.png) | ⇒ ![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png)  ![\iro[ak]{3} $$ \iro[ak]{3} $$](./eq/eq-ni-0d2932b6e42863b6345e67bb27901bb4.png) |
 ![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)  ![\iro[mr]{1y} $$ \iro[mr]{1y} $$](./eq/eq-ni-8e5a0bdbc6ae0340f33135f3f0a2bdb9.png)  ![\iro[pk]{6t} $$ \iro[pk]{6t} $$](./eq/eq-ni-ff6581ba1f6a6f984a72c0cf6beebf9d.png) | ⇒ ![\iro[pk]{\ppd{f}{t}} $$ \iro[pk]{\ppd{f}{t}} $$](./eq/eq-ni-088f059290225a1fed7cda1c2fbf8926.png)  ![\iro[pk]{6} $$ \iro[pk]{6} $$](./eq/eq-ni-cb431da695136bafbd053ca83b02c02d.png) | |
 ![\iro[ao]{1x} $$ \iro[ao]{1x} $$](./eq/eq-ni-b8d44956fe1fa2e07c37f0f3156eef34.png)    ![\iro[mr]{9t} $$ \iro[mr]{9t} $$](./eq/eq-ni-27d7c80343ecb1c1e735b721c2fb7529.png) | ⇒ ![\iro[mr]{\ppd{f}{t}} $$ \iro[mr]{\ppd{f}{t}} $$](./eq/eq-ni-907eadbab741099886ff2ddc100fa0fc.png)  ![\iro[mr]{9} $$ \iro[mr]{9} $$](./eq/eq-ni-ab7c00b616eb67326db34be5086c9cbe.png) | |
     ![\iro[ao]{11t} $$ \iro[ao]{11t} $$](./eq/eq-ni-d5afd8dfdfec76914aed26944a8959ab.png) | ⇒ ![\iro[ao]{\ppd{f}{t}} $$ \iro[ao]{\ppd{f}{t}} $$](./eq/eq-ni-bd06a061e32f7d1959c5b7d8d7cb2d55.png)  ![\iro[ao]{11} $$ \iro[ao]{11} $$](./eq/eq-ni-89dd7d1b96c0316f990f85ff4cb5e08b.png)  ![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) |
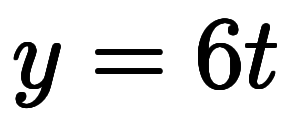 を
を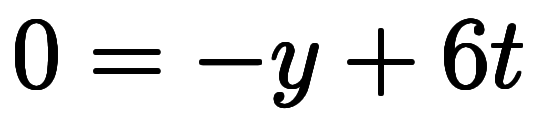 に変形して
に変形して の式に足せば
の式に足せば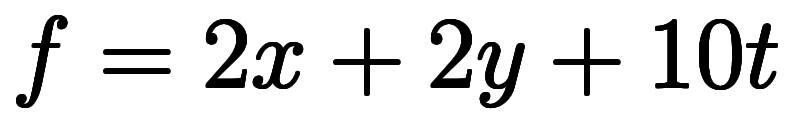 が得られる。このため、
が得られる。このため、

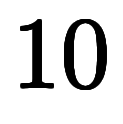 にもなれる。その気になれば無数の偏微分を作れる。例えば、こんな色のも作れる。
にもなれる。その気になれば無数の偏微分を作れる。例えば、こんな色のも作れる。 |  ![\iro[ao]{-1x} $$ \iro[ao]{-1x} $$](./eq/eq-ni-50cb19ee0a760e05bce3000bc7ad9ebd.png)    ![\iro[mz]{13t} $$ \iro[mz]{13t} $$](./eq/eq-ni-788f475f941814b0ab81b29c39bca992.png) | ⇒ ![\iro[mz]{\ppd{f}{t}} $$ \iro[mz]{\ppd{f}{t}} $$](./eq/eq-ni-d561006bbd7daafbd134b1cea555e789.png)  ![\iro[mz]{13} $$ \iro[mz]{13} $$](./eq/eq-ni-e8c6517be319a92794416fcf870c8512.png) |
 は不定値である。纏めると:
は不定値である。纏めると: の数を自由に変えられる
の数を自由に変えられる 以外に文字が無いときの偏微分が常微分である
以外に文字が無いときの偏微分が常微分である![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) と
と![\iro[ao]{\ddd{f}{t}} $$ \iro[ao]{\ddd{f}{t}} $$](./eq/eq-ni-3105d31bafa342246070375fe0b308e8.png) で区別できる。ただ、他の偏微分に気づいた人から混乱が始まる。この混乱を無くすには、色んな偏微分を厳密に書き分け、正しく整理する必要がある。そうすれば、自ずと偏微分と常微分を一貫した表記で書けるようになる。また、書き表せないものを書けるようになったとき、新しい発想ができるようになるかもしれない。実際、熱力学では赤と青の他、紫に相当する偏微分も登場する。そのため、
で区別できる。ただ、他の偏微分に気づいた人から混乱が始まる。この混乱を無くすには、色んな偏微分を厳密に書き分け、正しく整理する必要がある。そうすれば、自ずと偏微分と常微分を一貫した表記で書けるようになる。また、書き表せないものを書けるようになったとき、新しい発想ができるようになるかもしれない。実際、熱力学では赤と青の他、紫に相当する偏微分も登場する。そのため、 よりも強力な偏微分表記が用いられている。それでも全ての偏微分を書き分けるには不十分であるが、次回は、その強力な表記を通じて偏微分の意味について確認しておく。
よりも強力な偏微分表記が用いられている。それでも全ての偏微分を書き分けるには不十分であるが、次回は、その強力な表記を通じて偏微分の意味について確認しておく。