![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分と常微分の違い のバックアップ(No.4) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
偏微分と常微分の違い のバックアップ(No.4) |
偏微分と常微分の違いを問われて、多くの人は「固定する変数の有無」と答える。 定義式を眺めば頷ける。
ここで言う「固定する変数」とは偏微分の方に現れる赤い「 しかし、その違いは関数 実際、1変数関数は2変数関数の特殊例と見なすことができ、その偏微分は常微分に一致する。
この疑問に答えるには、同じ関数に対し その答えは「EMANの物理学/解析力学/全微分/偏微分と常微分の違い*1」でやっと見つかった。 偏微分と常微分の違いまず、準備として、2変数関数
ここで、
恐らく、偏微分を急いで学ぶ人にとって、これが同じ関数 ここまでは多くのテキストで述べられている。しかし、この式では、「分母」が まず、
次ぎに、
ここで、
EMANの物理では話しがココで終りである。しかし、さらに一歩踏み込んで式の意味を読み取ろうとすると、微分表記
|
|
しかし、今度は を代入しても
を代入しても が
が と
と の関数にはなるが、
の関数にはなるが、 だけの関数にはならない。このため、精々次のようにな偏微分しか存在しない。
だけの関数にはならない。このため、精々次のようにな偏微分しか存在しない。
|
同様に、 が
が と
と と
と の影響を受ける限り、どの項も消えず
の影響を受ける限り、どの項も消えず![\iro[ao]{\ppd{f}{t}} $$ \iro[ao]{\ppd{f}{t}} $$](./eq/eq-ni-bd06a061e32f7d1959c5b7d8d7cb2d55.png)

![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png) となる。
となる。
 の限界、その2
の限界、その2 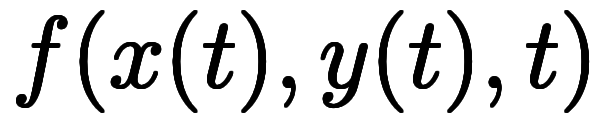 の具体例を考えてみよう。
の具体例を考えてみよう。
|
まず、 のため、
のため、

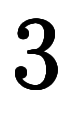 は間違いない。
は間違いない。
次ぎに、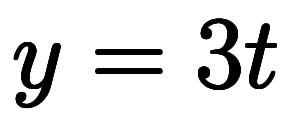 を
を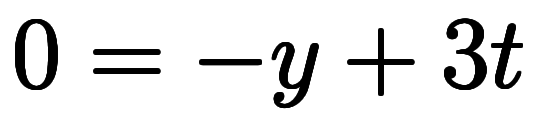 に変形して
に変形して の式に足せば
の式に足せば が得られる。このため、
が得られる。このため、

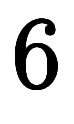 にもなれる。
にもなれる。
以下では、これまでの問題を直観的に説明してみる。
まず、![f = \iro[md]{1x} + \iro[ao]{2y} + \iro[ak]{3t} $$ f = \iro[md]{1x} + \iro[ao]{2y} + \iro[ak]{3t} $$](./eq/eq-ni-7f80055027a63fcd4a9f189db7b9e139.png) を
を![f = \iro[md]{x} + \iro[ao]{y} + \iro[ao]{y} + \iro[ak]{t} + \iro[ak]{t} + \iro[ak]{t} $$ f = \iro[md]{x} + \iro[ao]{y} + \iro[ao]{y} + \iro[ak]{t} + \iro[ak]{t} + \iro[ak]{t} $$](./eq/eq-ni-5838baab5c717f4cf49099137077f2fa.png) に変形する。
に変形する。
すると、自ずと![df = \iro[md]{dx} + \iro[ao]{dy} + \iro[ao]{dy} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$ df = \iro[md]{dx} + \iro[ao]{dy} + \iro[ao]{dy} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$](./eq/eq-ni-19b794233a95dfdbb8149a79c942bf9e.png) が得られる。
が得られる。
偏微分

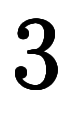 というのは、
というのは、 の個数を表す。
の個数を表す。
 に
に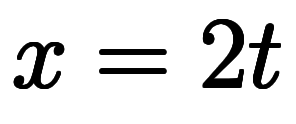 と
と を代入すると、
を代入すると、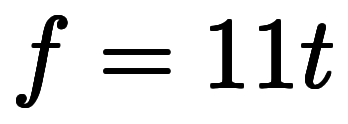 となる。
となる。
全微分は![df = \iro[md]{dt} + \iro[md]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$ df = \iro[md]{dt} + \iro[md]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$](./eq/eq-ni-5cca288749a0d738e58e9c02a247fbf7.png) 。
。
常微分

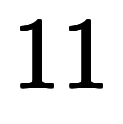 は全ての
は全ての の個数を表す。
の個数を表す。
次ぎに、限界その1では のみを適応して、
のみを適応して、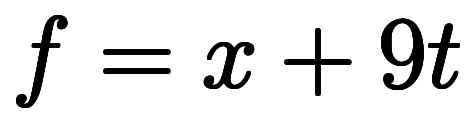 となる。
となる。
全微分は![df = \iro[md]{dx} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$ df = \iro[md]{dx} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$](./eq/eq-ni-3886f7b3ef4898c40b2e9efaa7284dc6.png) 。
。
登場した青い偏微分は![\iro[ao]{dy} $$ \iro[ao]{dy} $$](./eq/eq-ni-c594c98f7b472814d977dfd12fd44681.png) と
と![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png) の分を数えた
の分を数えた![\iro[ao]{\ppd{f}{t}} $$ \iro[ao]{\ppd{f}{t}} $$](./eq/eq-ni-bd06a061e32f7d1959c5b7d8d7cb2d55.png)

 である。
である。
対して、赤い偏微分は![\iro[ak]{dt} $$ \iro[ak]{dt} $$](./eq/eq-ni-024b3fcb224faff14eed289b902d46f8.png) の分のみを数えた
の分のみを数えた![\iro[ak]{\ppd{f}{t}} $$ \iro[ak]{\ppd{f}{t}} $$](./eq/eq-ni-a9f04482acc579f710fe583a5f6d1172.png)

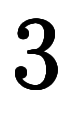 である。
である。
続けて、限界その2では1つの だけを
だけを に変換して
に変換して を作った。
を作った。
全微分は![df = \iro[md]{dx} + \iro[ao]{dy} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$ df = \iro[md]{dx} + \iro[ao]{dy} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ao]{dt} + \iro[ak]{dt} + \iro[ak]{dt} + \iro[ak]{dt} $$](./eq/eq-ni-c8eaf818821e6fc0155900aba27ac09d.png) 。
。
登場した偏微分は変換された![\iro[ao]{dy} $$ \iro[ao]{dy} $$](./eq/eq-ni-c594c98f7b472814d977dfd12fd44681.png) と
と![\iro[ao]{dt} $$ \iro[ao]{dt} $$](./eq/eq-ni-5482baaaafd3dfb95bf127b8566d6084.png) の分を数えた
の分を数えた

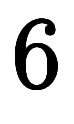 である。
である。
以上を図に纏めると次のようになる:
【編集中: を数える図】
を数える図】