![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
冪乗・冪根・対数の表記 のバックアップ(No.2) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
冪乗・冪根・対数の表記 のバックアップ(No.2) |
現行表記 |
|||||||||||||||||||||||||||||||||||||||
| 演算 | 現行表記 | 添字表記 |
|---|---|---|
| 冪乗 |  |  |
| 冪根 | ![\rt[b]{c} $$ \rt[b]{c} $$](./eq/eq-ni-d1148a38743032389d72eeab4f02bb6d.png) |  |
| 対数 |  |  |
代わりに、 と
と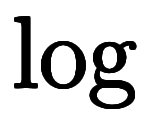 を省いた最大の利点として、不要な飾りに惑わされずに済む。
を省いた最大の利点として、不要な飾りに惑わされずに済む。
その上で、添え字表記に揃えることで、幾つかの性質が形式的にも簡潔に見える。



一般に、冪乗 を基準に、冪根
を基準に、冪根![\rt[b]{c}=a $$ \rt[b]{c}=a $$](./eq/eq-ni-cba096b96e4780aab885c193b2076ecc.png) と対数
と対数 はその左側と右側を求める逆算と言う。
はその左側と右側を求める逆算と言う。
3量の相互関係であるため、冪根と対数もまた互いに逆演算と言える。
逆演算の場合は、重ねると演算が打ち消して元に戻る性質を持つ。
| 正演算&逆演算 | 現行表記 | 添字表記 | |
|---|---|---|---|
| 冪乗→冪根 | ![\rt[b]{a^b}=a $$ \rt[b]{a^b}=a $$](./eq/eq-ni-2988b16fbfd2734a949d3448cfd85496.png) | 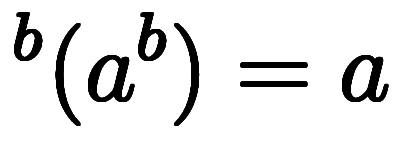 |  |
| 冪根→冪乗 | ![{\rt[b]a}^b=a $$ {\rt[b]a}^b=a $$](./eq/eq-ni-4324ae96e5f0bbe57c6826f1ec0e16c9.png) |  | |
| 冪乗→対数 |  | 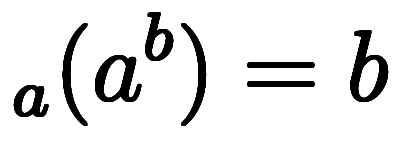 | |
| 対数→冪乗 | 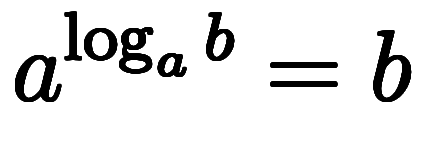 |  | |
| 対数→冪乗 | ![\rt[\log_a{c}]{c} = a $$ \rt[\log_a{c}]{c} = a $$](./eq/eq-ni-f4ab69cfe3ac279c209a2c07240e1f09.png) | 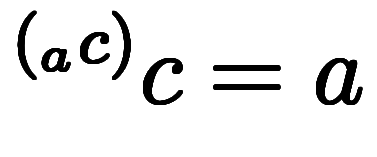 | |
| 冪根→対数 | ![\log_{\rt[b]{c}}c = b $$ \log_{\rt[b]{c}}c = b $$](./eq/eq-ni-e6efd21dec5890de5f4f4fed119ec5bc.png) | 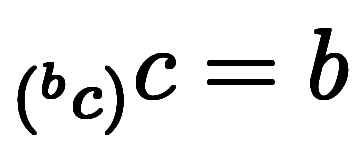 | |