![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
出合い算 のバックアップ(No.1) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
出合い算 のバックアップ(No.1) |
例題 |
Aの速度: |
Bの速度: |
相対距離: |
Cの速度: |
ここから、
相対速度: |
出合時間: |
飛行距離: |
よって、答え:240 km。



この問題を代数で考えると図1のようになる。
| 図1:時空間図 |
|---|
| File not found: "出合い算01.png" at page "出合い算"[添付] |
時間と位置のグラフを時空間図というが、横軸が時間の進み、縦軸が位置になる。移動した軌跡が線として現われる。図1では A と B を青い線、C を赤い線で表している。また、速さは向きと合わせて速度として軌跡線の傾きとして現われる。
図1では、時間は進む向きを正、位置には北を正としている。B の居る場所を基準にすると、 =0km、
=0km、 =300km、
=300km、 =150km になる。速度は、Aが
=150km になる。速度は、Aが =−75km/h、Bが
=−75km/h、Bが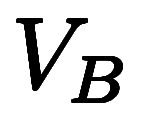 =+80km/h、Cが
=+80km/h、Cが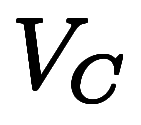 =±120km/h となる。特に C は速さが同じでも、AやBに出合う度に向きを逆転するため、速度は+120km/hのときと−120km/hのときに分かれる。しかし、向きも合わせて
=±120km/h となる。特に C は速さが同じでも、AやBに出合う度に向きを逆転するため、速度は+120km/hのときと−120km/hのときに分かれる。しかし、向きも合わせて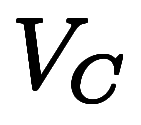 と置き、計算するときに値を変えるのが代数のヤリ方である。
と置き、計算するときに値を変えるのが代数のヤリ方である。
そして、A、B、Cが動きだし、C が A に出合うまでの時間を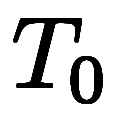 、その時Aの位置を
、その時Aの位置を 、Bの位置を
、Bの位置を として、さらに動き続け、C が B に出合うまでの時間を
として、さらに動き続け、C が B に出合うまでの時間を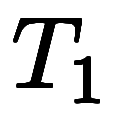 、その時Aの位置を
、その時Aの位置を 、Bの位置を
、Bの位置を として、A と B が出合うまで鳥 C を追い続けば、答えが求まる。
として、A と B が出合うまで鳥 C を追い続けば、答えが求まる。
具体的に、 、
、 、
、 、
、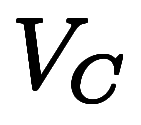 から
から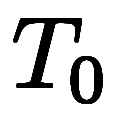 が
が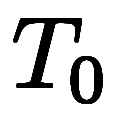

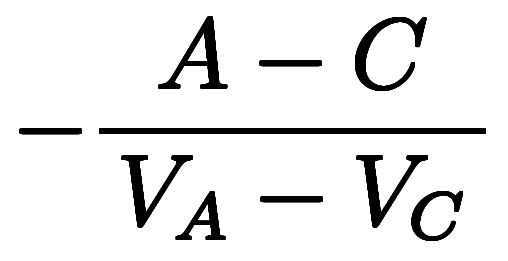 として求まる。
として求まる。
そのとき、




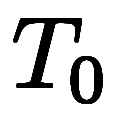 、
、



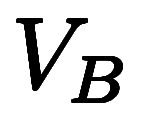
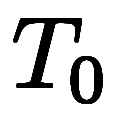 で求まる。
で求まる。
また、Cの進む距離は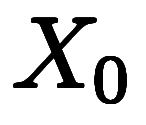

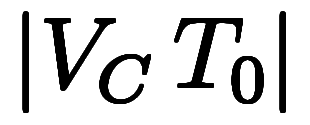 と求まる。
と求まる。
今、鳥が から
から に移り、今度は
に移り、今度は に居るBに向かって進む。このため、上の式に対し、
に居るBに向かって進む。このため、上の式に対し、 ⇒
⇒ 、
、 ⇒
⇒ に置換して、同様に計算を進められる。
に置換して、同様に計算を進められる。
結果として、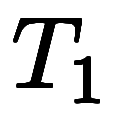

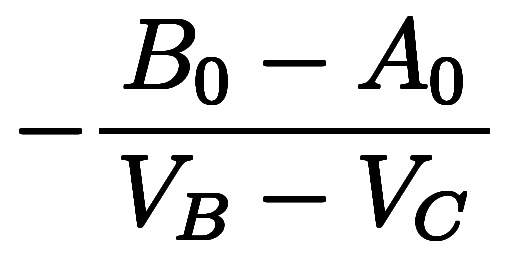 、
、




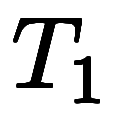 、
、



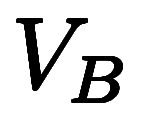
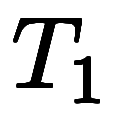 、
、

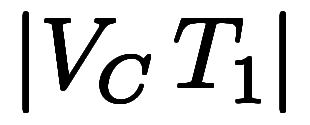 。
。
同様に、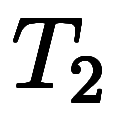

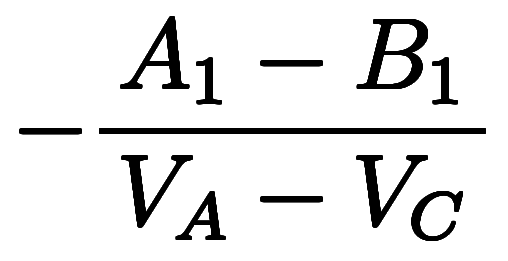 、
、




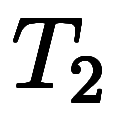 、
、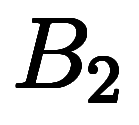



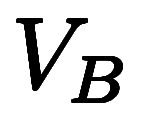
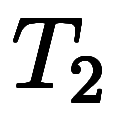 、
、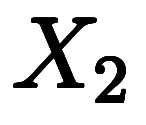

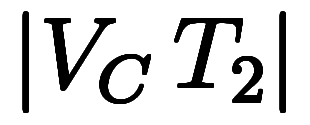 。
。
計算結果を表にすると次のようになる:
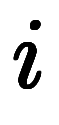 | 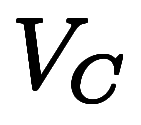 |  |  | 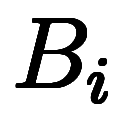 |  | 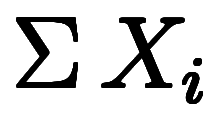 |
| 0 | +120 km/h | 0.789 h | 244.737 km | 63.158 km | 94.737 km | 94.737 km |
| 1 | -120 km/h | 0.908 h | 181.184 km | 135.789 km | 108.974 km | 203.684 km |
| 2 | +120 km/h | 0.239 h | 164.460 km | 154.903 km | 28.670 km | 232.355 km |
| 3 | -120 km/h | 0.048 h | 161.115 km | 158.726 km | 5.734 km | 238.089 km |
| 4 | +120 km/h | 0.013 h | 160.235 km | 159.732 km | 1.509 km | 239.598 km |
| 5 | -120 km/h | 0.003 h | 160.059 km | 159.933 km | 0.301 km | 239.899 km |
| … | … | … | … | … | … | … |
一番右の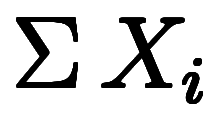 は
は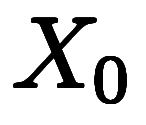 から
から までの合計で、今回の求める答えである。しかし、段々と答えの 240km に近づいていくものの、毎回近づける量
までの合計で、今回の求める答えである。しかし、段々と答えの 240km に近づいていくものの、毎回近づける量 も段々小さくなって、中々240kmにはならない。もっとも、AとBが出合って
も段々小さくなって、中々240kmにはならない。もっとも、AとBが出合って =
=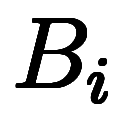 になることもなく、計算自体が終わらない。実際、
になることもなく、計算自体が終わらない。実際、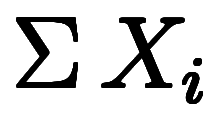 はこの後 239.979 ⇒ 239.995 ⇒ 239.999 ⇒ と永遠に続く。
はこの後 239.979 ⇒ 239.995 ⇒ 239.999 ⇒ と永遠に続く。
図で言うと、赤い折れ線はAとBの軌跡の間をずっと往復するが、AとBが出合う青い線の交点にピタッと辿り付くことが無く、往復が終わらない。
この方法は数値計算と呼ばれて、問題が複雑すぎて簡単に計算できないときに使われる。この場合、十分の桁数を計算したら計算を打ち切り、近似値で答えることになるが、例えば、5回目で打ち切る場合、必要な桁数に応じて 239.899 km、239.900、239.90 または 240 などで答えることになる。



では、最初にやった算数の時空間図を考えてみよう。
| 図2:時空間図(算数版) |
|---|
| File not found: "出合い算02.png" at page "出合い算"[添付] |
AとBがそれぞれ と
と から出発し、速度
から出発し、速度 と
と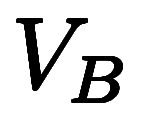 で走り、時間
で走り、時間 の後で出合う。ここまでは普通であるが、問題は速さの扱いである。
の後で出合う。ここまでは普通であるが、問題は速さの扱いである。
速さは速度の絶対値であり、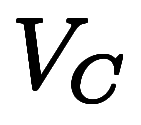 が+120kmのときも−120kmのときも120kmのままである。このため、赤い実線が折れ曲がり、−120kmで右下に向かって進むとき、赤い点線のように無理やり+120kmとして進ませば、
が+120kmのときも−120kmのときも120kmのままである。このため、赤い実線が折れ曲がり、−120kmで右下に向かって進むとき、赤い点線のように無理やり+120kmとして進ませば、 になるまで進んだ距離が答えの
になるまで進んだ距離が答えの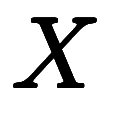 になる。さらに、点線はずっと同じ速度+120km/hで進むため、
になる。さらに、点線はずっと同じ速度+120km/hで進むため、 は
は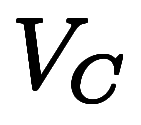 と
と の単純乗算で求まる。
の単純乗算で求まる。