![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/ベクトル積分演算子 のバックアップ(No.2) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/ベクトル積分演算子 のバックアップ(No.2) |
ベクトル積分と置換積分公式 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 分数形 | 演算子形 | |
|---|---|---|
![\inte[R] \ffd{\b F\,dx}{d} $$ \inte[R] \ffd{\b F\,dx}{d} $$](./eq/eq-ni-64e51e04b09c6f43c4541f9886d7e75c.png) | ![\inte[R] \ffd{dx}{d} \b F $$ \inte[R] \ffd{dx}{d} \b F $$](./eq/eq-ni-608bbdcc9e2dd056e8429a7513a3c448.png) | ![\inte[R] d^-\!\!dx\,\b F $$ \inte[R] d^-\!\!dx\,\b F $$](./eq/eq-ni-27fda508e9a8e8922472078ca6d57dc5.png) |



3次元における線積分、面積分、体積分の微小要素を成分で書くと、線要素 =
=![\!\left[\begin{array}{c} dx \\ dy \\ dz \end{array}\right]\! $$ \!\left[\begin{array}{c} dx \\ dy \\ dz \end{array}\right]\! $$](./eq/eq-ni-14c1dbc462f83fd3a28dc2e0f4ef3abf.png) 、面要素
、面要素 =
=![\!\left[\begin{array}{c} dydz \\ dzdx \\ dxdy \end{array}\right]\! $$ \!\left[\begin{array}{c} dydz \\ dzdx \\ dxdy \end{array}\right]\! $$](./eq/eq-ni-26b34d17e0dc834680b058a003f9b56b.png) 、体要素
、体要素 =
= 。等式の両辺で
。等式の両辺で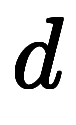 の数が異なるのが問題。微分では
の数が異なるのが問題。微分では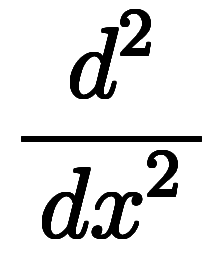 が2階微分を表すように、
が2階微分を表すように、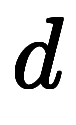 の数は微分の階数。同様に、猫式表記では
の数は微分の階数。同様に、猫式表記では は積分を表し、
は積分を表し、 の数は積分の階数。これら階数が冒頭にあった「次元」の実体で、「次元」を超える置換積分では階数が変化する。このため、微小要素の表記次第で階数が変わっては困る。
の数は積分の階数。これら階数が冒頭にあった「次元」の実体で、「次元」を超える置換積分では階数が変化する。このため、微小要素の表記次第で階数が変わっては困る。
これを回避するため、猫式では微小要素の記号に階数を記入する。 ⇒
⇒ 、
、 ⇒
⇒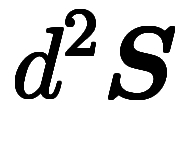 、
、 ⇒
⇒ 。また、それぞれの積分には対応して
。また、それぞれの積分には対応して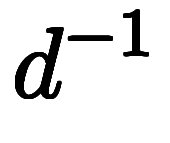 、
、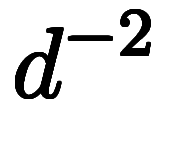 、
、 を使う。ただし、1階の場合は省略して
を使う。ただし、1階の場合は省略して のままも可とする。
のままも可とする。
以上の規則を導入すると、各積分は次のようになる。
| 分数形 | 演算子形 | ||
|---|---|---|---|
| 線積分 | ![\inte[R] \ffd{\b F \sx d^1\b r}{d^1} $$ \inte[R] \ffd{\b F \sx d^1\b r}{d^1} $$](./eq/eq-ni-9b570a97d4b631c9e12c27e4a44e3838.png) | ![\inte[R] \ddd{^1\b r}{^1} \sx \b F $$ \inte[R] \ddd{^1\b r}{^1} \sx \b F $$](./eq/eq-ni-890f3b549d3687f278fdb72ba6dad9a5.png) | ![\inte[R] d^{-1}d^1 \b r \sx \b F $$ \inte[R] d^{-1}d^1 \b r \sx \b F $$](./eq/eq-ni-845f0a75c60360ed3583393f426de81f.png) |
| 面積分 | ![\inte[S] \ffd{\b F \sx d^2\b S}{d^2} $$ \inte[S] \ffd{\b F \sx d^2\b S}{d^2} $$](./eq/eq-ni-44db6f7202186262b17c951ab0901a41.png) | ![\inte[S] \ddd{^2\b S}{^2} \sx \b F $$ \inte[S] \ddd{^2\b S}{^2} \sx \b F $$](./eq/eq-ni-30784ee21f78b08d83e0593e26237d2e.png) | ![\inte[R] d^{-2}d^2 \b S \sx \b F $$ \inte[R] d^{-2}d^2 \b S \sx \b F $$](./eq/eq-ni-e87d4f43bfa13efe1d54b4b565804b19.png) |
| 体積分 | ![\inte[V] \ffd{\b F \, d^3 V}{d^3} $$ \inte[V] \ffd{\b F \, d^3 V}{d^3} $$](./eq/eq-ni-1fefb89a1ee34a0c3c34c511e55abf8f.png) | ![\inte[V] \ddd{^3 V}{^3} \, \b F $$ \inte[V] \ddd{^3 V}{^3} \, \b F $$](./eq/eq-ni-a9776710c04a65f7cacffeb5cdbc3355.png) | ![\inte[R] d^{-3}d^3 V \, \b F $$ \inte[R] d^{-3}d^3 V \, \b F $$](./eq/eq-ni-86666975fafa2fffdc7788b400d2f52c.png) |



猫式では置換積分は次のように書き換わる。
| 通常表記 | 猫式表記 | |
|---|---|---|
| ストークスの定理 | ![\inte[R] \b F \sx d\b r $$ \inte[R] \b F \sx d\b r $$](./eq/eq-ni-5fad66952913cdb79c319e6bc2e1d6d7.png) = =![\inte[S] \nabla \vx \b F \sx d\b S $$ \inte[S] \nabla \vx \b F \sx d\b S $$](./eq/eq-ni-64ace8ceb1570e0f1535a1d7517e72d1.png) | ![\inte[R] \ddd{^1\b r \sx}{^1} \b F $$ \inte[R] \ddd{^1\b r \sx}{^1} \b F $$](./eq/eq-ni-683d6ba3cf238eac155cffca0217c170.png) = =![\inte[S] \ddd{^2\b S \sx}{^2} \ddd{\,\vx}{\b r} \b F $$ \inte[S] \ddd{^2\b S \sx}{^2} \ddd{\,\vx}{\b r} \b F $$](./eq/eq-ni-382a06dd1bc1da224a67bfe37b2a7629.png) |
| ガウスの定理 | ![\inte[S] \b F \sx d\b S $$ \inte[S] \b F \sx d\b S $$](./eq/eq-ni-297029a07ea1238a9ca1eee66f79d173.png) = =![\inte[V] \nabla \sx \b F \, d V $$ \inte[V] \nabla \sx \b F \, d V $$](./eq/eq-ni-6f4e537470e94b9400bf5daa3b1b7868.png) | ![\inte[S] \ddd{^2\b S \sx}{^2} \b F $$ \inte[S] \ddd{^2\b S \sx}{^2} \b F $$](./eq/eq-ni-66290dd45bc242700ead4330b0708859.png) = =![\inte[V] \ddd{^3 V }{^3} \ddd{\,\sx}{\b r} \b F $$ \inte[V] \ddd{^3 V }{^3} \ddd{\,\sx}{\b r} \b F $$](./eq/eq-ni-f315ae810d2e2e6aaf984779a1a6e9ba.png) |
作用対象の を抜けば、演算子の等価変換となる。
を抜けば、演算子の等価変換となる。
ストークスの定理:![\inte[R] \ddd{^1\b r \sx}{^1} $$ \inte[R] \ddd{^1\b r \sx}{^1} $$](./eq/eq-ni-27579130f0f62efc220b03025e7cd18a.png) =
=![\inte[S] \ddd{^2\b S \sx}{^2} \ddd{\,\vx}{\b r} $$ \inte[S] \ddd{^2\b S \sx}{^2} \ddd{\,\vx}{\b r} $$](./eq/eq-ni-ecd2165d33f2305ccdac078e4dfbe65b.png)
ガウスの定理:![\inte[S] \ddd{^2\b S \sx}{^2} $$ \inte[S] \ddd{^2\b S \sx}{^2} $$](./eq/eq-ni-97ae034cb734aa9cfdd1b0c45c35eb6d.png) =
=![\inte[V] \ddd{^3 V }{^3} \ddd{\,\sx}{\b r} $$ \inte[V] \ddd{^3 V }{^3} \ddd{\,\sx}{\b r} $$](./eq/eq-ni-f2dadb2e88032b69bcbf8d36dfd4a72c.png)
演算子としては成立すべき式ではあるが、残念ながらベクトル演算のみでは導けない。したがって、今回の真面目な話はココまで。



ここからはふざけててみます。外積代数を習うまでに苦労して開発したイカサマ計算なり。



先に偶然に成立してしまうガウスの定理から。
ガウスの定理の右辺= | |
= | 分離形で、倍積内積の結合則 |
= | 成分表示 |
= | 倍積実行、除算実行 |
= |
|
= | 累次積分に変形して積分実行 |
= | 積分領域再解釈 |
= |



続いて、同じ手順をストークスの定理に。
ストークスの定理の右辺= | |
= | 分離形で、スカラ三重積の置換則 |
= | 成分表示 |
= | 外積実行、除算実行 |
= |
はい、外積と除算の結果、ゼロ。



上の計算は、実は初っぱなのスカラ三重積からもう成立してない。しかし、逆から計算すれば分かるが、減算の項さえなければ成立する、という非常に惜しい形で破綻している。
このため、
イカサマ規則:微小要素に関わるベクトル演算で、減算項を に書き換える。これで、とりあえず計算は通せる。
に書き換える。これで、とりあえず計算は通せる。
そもそも論すらないが、証拠。
⇒ | イカサマ外積実行、 |
= |
|
= | 累次積分に変形して積分実行 |
= | 積分領域再解釈 |
= |



このイカサマ規則は、ストークスの定理を両辺から計算し、違いを吸収するルールとして導入した。目的は、あくまでも3次元ベクトル演算の範囲内で、図を借りずに置換積分を得るだった。上では細かく書いているが、 =
=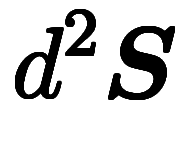 、
、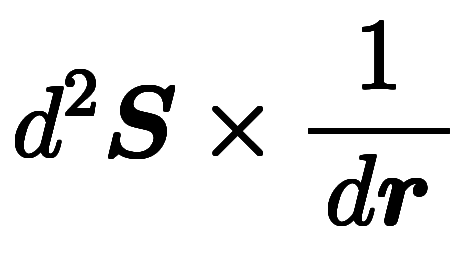 =
= のセンスさえ持っていれば、次のように飛ばせる。
のセンスさえ持っていれば、次のように飛ばせる。
ガウスの定理:![\inte[V] \ffd{1}{d^3} d^3V \left( \ffd{1}{d\b r} \sx d \b F \right) $$ \inte[V] \ffd{1}{d^3} d^3V \left( \ffd{1}{d\b r} \sx d \b F \right) $$](./eq/eq-ni-40cf1859db14e630e4e99a892eda23b3.png) =
=![\inte[V] \ffd{1}{d^2} \ddd{^3V}{\b r} \sx \ddd{\b F}{} $$ \inte[V] \ffd{1}{d^2} \ddd{^3V}{\b r} \sx \ddd{\b F}{} $$](./eq/eq-ni-c3f5b22af698789ca2f86495ade634be.png) =
=![\inte[S] \ffd{1}{d^2} d^2S \sx \b F $$ \inte[S] \ffd{1}{d^2} d^2S \sx \b F $$](./eq/eq-ni-fe64399ff7e41bf7a398923c55f914ff.png)
ストークスの定理:![\inte[S] \ffd{1}{d^2} d^2\b S \sx \left( \ffd{1}{d\b r} \vx d \b F \right) $$ \inte[S] \ffd{1}{d^2} d^2\b S \sx \left( \ffd{1}{d\b r} \vx d \b F \right) $$](./eq/eq-ni-9a4c75a9d9422dc64a7a18477992aa80.png) =
=![\inte[S] \ffd{1}{d^2} d \b F \sx \left( d^2\b S \vx \ffd{1}{d\b r} \right) $$ \inte[S] \ffd{1}{d^2} d \b F \sx \left( d^2\b S \vx \ffd{1}{d\b r} \right) $$](./eq/eq-ni-e246298c8ea30d478997a0cd217394b6.png) =
=![\inte[R] \ffd{1}{d } \b F \sx d\b r $$ \inte[R] \ffd{1}{d } \b F \sx d\b r $$](./eq/eq-ni-c0881b9ac6f652295d9a3506a42e3755.png)
さらに、このイカサマも捨てたものではない。実は、ベクトルの次元に関係無く、積分の「次元」を跨がる全ての置換積分に効く。ガウスの定理も減算項が無かったためにイカサマせずに済んだようなもの。微分形式と外積代数から、このイカサマもまた意味を持っていることが分かる。
というわけで、次回は微分形式と外積代数を導入。でも、タイトルは基底成分表記(仮)。