![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/ベクトル微分演算子 のバックアップ(No.4) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/ベクトル微分演算子 のバックアップ(No.4) |
|
||||||||||||||||||||||||||||
| 流派 | 勾配 | 回転 | 発散 | |
|---|---|---|---|---|
| 文字名 | 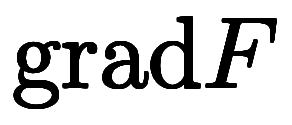 | 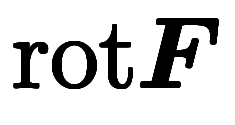 | 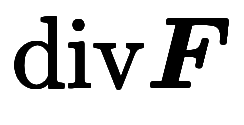 | |
| ナブラ |  | 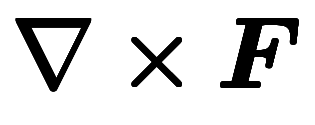 | 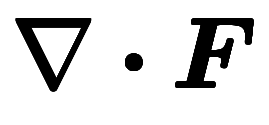 | |
| 猫式 | 分数形 |  | 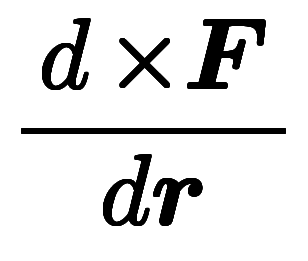 | 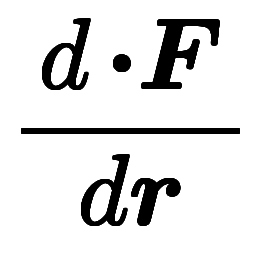 |
| 演算子形 | 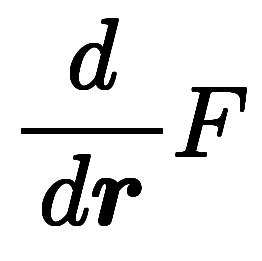 | 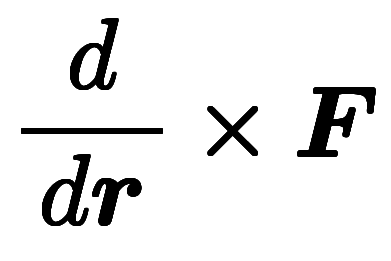 |  | |
| 分離形 | 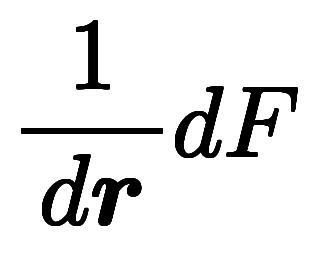 | 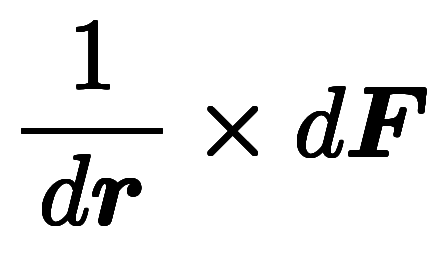 | 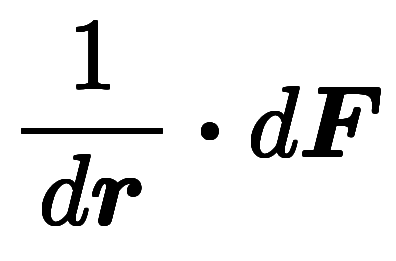 | |



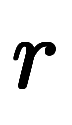 がスカラの場合、
がスカラの場合、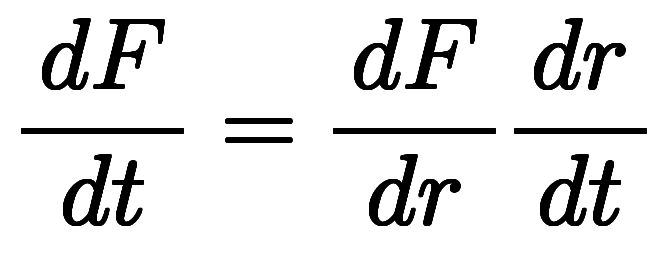 が
が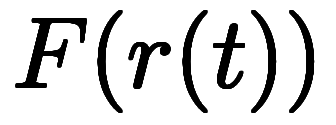 に対する連鎖則。分数形で記述する場合、あくまでも形式的だが、約分の感覚で直観的に式変形できる。
に対する連鎖則。分数形で記述する場合、あくまでも形式的だが、約分の感覚で直観的に式変形できる。
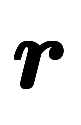 がベクトルの場合、
がベクトルの場合、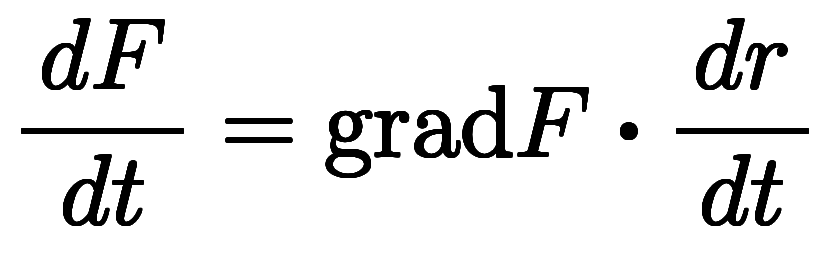 が
が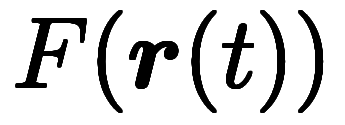 に対する連鎖則。ナブラを使っても
に対する連鎖則。ナブラを使っても 。微分に関しては、文字名もナブラも表現力に差はない。
。微分に関しては、文字名もナブラも表現力に差はない。
猫式分数形で書けば、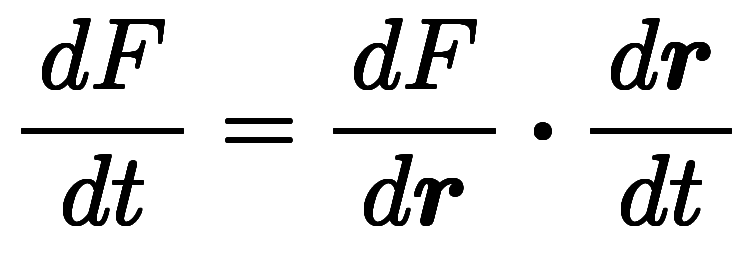 になる。スカラの積がスカラ内積になることを除けば、連鎖則の姿がそのまま生き残り、式を直観的に操作できる。
になる。スカラの積がスカラ内積になることを除けば、連鎖則の姿がそのまま生き残り、式を直観的に操作できる。



外積勾配の公式: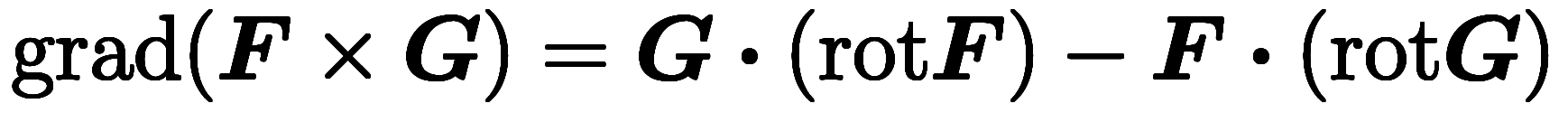
ナブラを使う場合、微分対積の分配則とスカラー三重積の交換則で計算可能。ただし、計算途中で作用対象が離れるため、工夫が必要。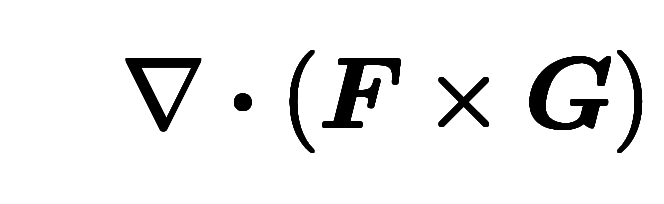
 // 微分対乗算の分配則
// 微分対乗算の分配則 // スカラ三重積の交換則
// スカラ三重積の交換則 // クロス外積の交代則
// クロス外積の交代則
一方、分離形表記では次のように記述可能。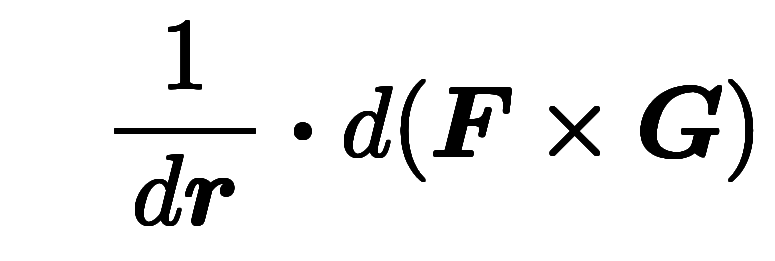
 // 微分対乗算の分配則
// 微分対乗算の分配則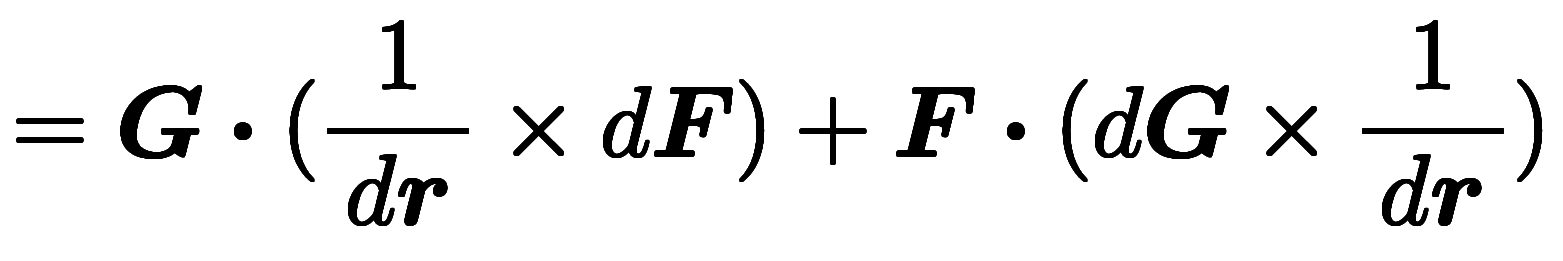 // スカラ三重積の交換則
// スカラ三重積の交換則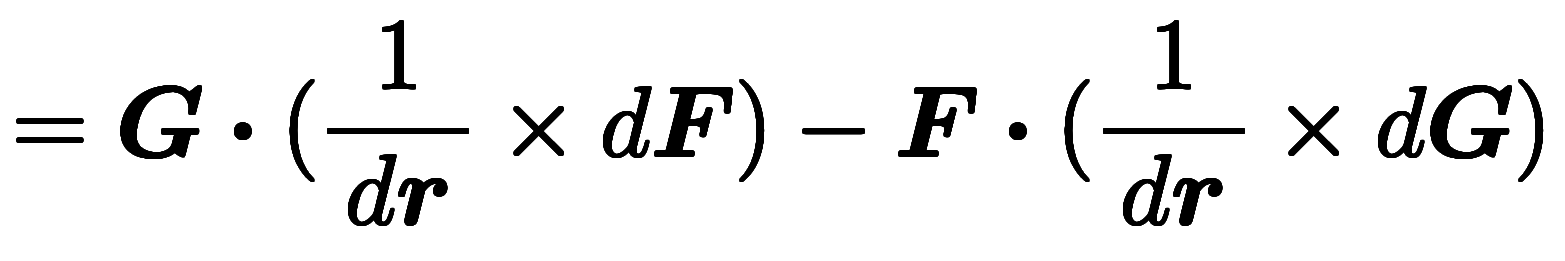 // クロス外積の交代則
// クロス外積の交代則