![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/基底成分表記 のバックアップ(No.2) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/基底成分表記 のバックアップ(No.2) |
混合基底 |
|
|
= | = |
= | = |
結果として、基底1を略せば、直感的にスカラを各成分に分配できる。
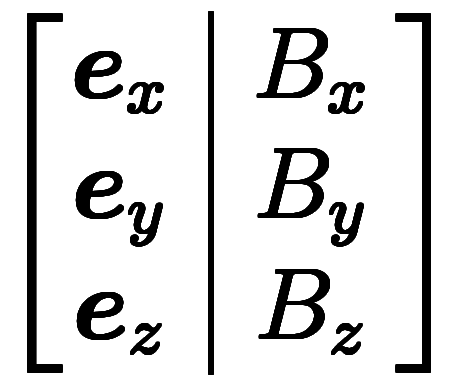 =
=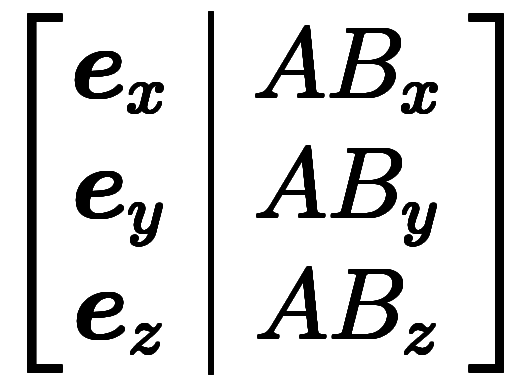
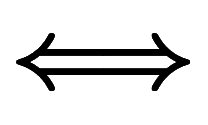

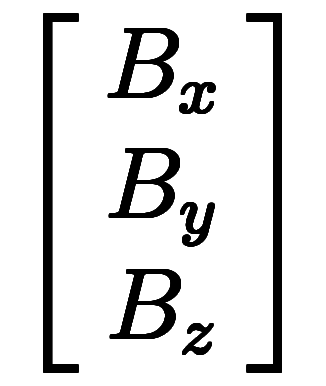 =
=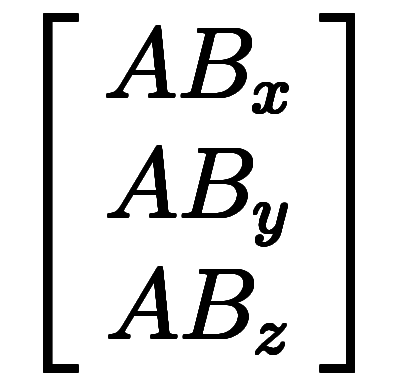



|
|
= |
|
= |
|
= |
|
結果として、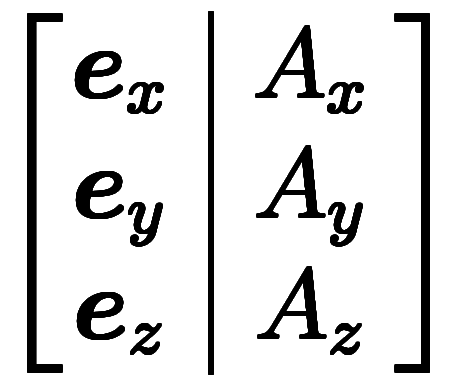

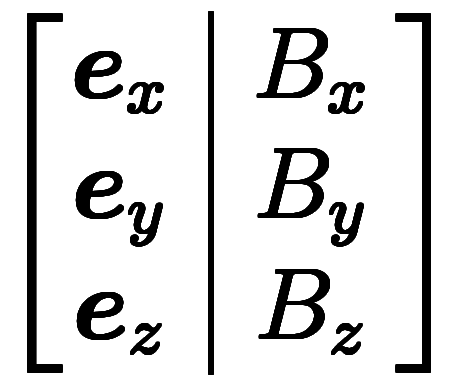 =
=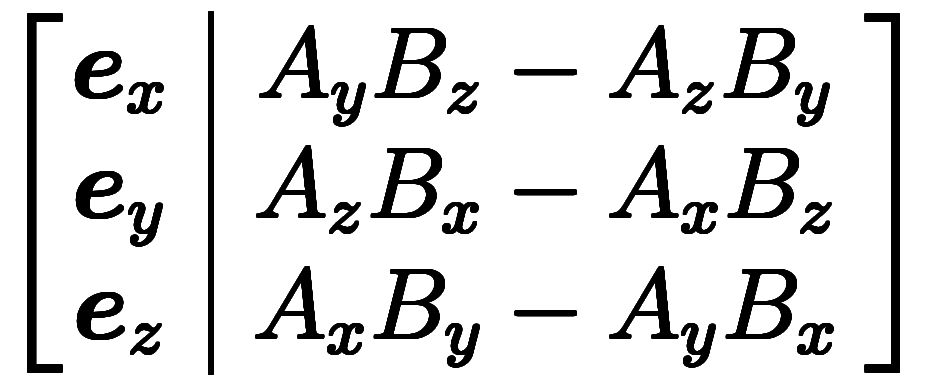

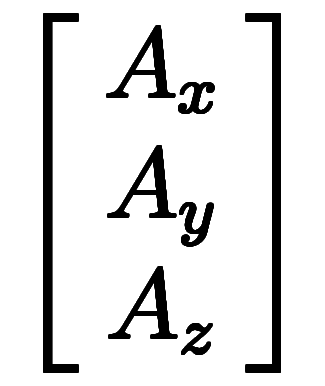

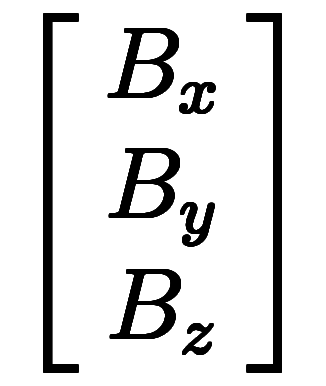 =
=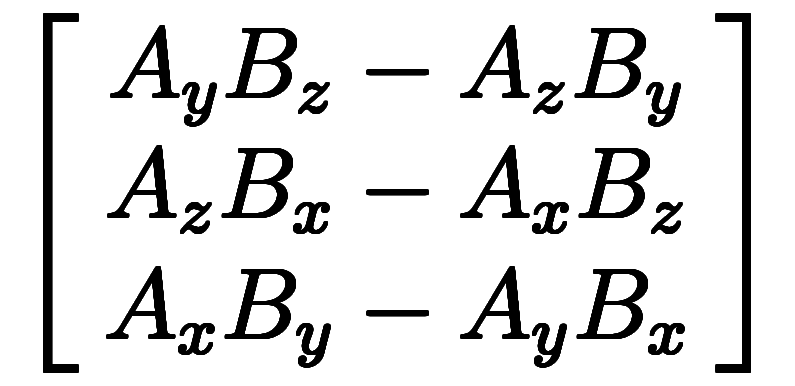
基底成分表記で覚えるなら、先に基底を埋め、輪環順で加算項を埋め、逆順で減算項を埋めると良い。![\arrb{ \b e_{\clr[gr]{x}} & \phantom{ A_y B_z - A_z B_y } \\ \b e_{\clr[gr]{y}} & \phantom{ A_z B_x - A_x B_z } \\ \b e_{\clr[gr]{z}} & \phantom{ A_x B_y - A_y B_x } } $$ \arrb{ \b e_{\clr[gr]{x}} & \phantom{ A_y B_z - A_z B_y } \\ \b e_{\clr[gr]{y}} & \phantom{ A_z B_x - A_x B_z } \\ \b e_{\clr[gr]{z}} & \phantom{ A_x B_y - A_y B_x } } $$](./eq/eq-ni-393cce550ac02e3d98a63ce743bb1b49.png) ⇒
⇒![\arrb{ \b e_{\clr[gr]{x}} & A_{\clr[gr]{y}} B_{\clr[gr]{z}} \phantom{ - A_z B_y } \\ \b e_{ y } & A_{ z } B_{ x } \phantom{ - A_x B_z } \\ \b e_{ z } & A_{ x } B_{ y } \phantom{ - A_y B_x } } $$ \arrb{ \b e_{\clr[gr]{x}} & A_{\clr[gr]{y}} B_{\clr[gr]{z}} \phantom{ - A_z B_y } \\ \b e_{ y } & A_{ z } B_{ x } \phantom{ - A_x B_z } \\ \b e_{ z } & A_{ x } B_{ y } \phantom{ - A_y B_x } } $$](./eq/eq-ni-90fb3dd7229e1dd0ef3aa98f7c0bdf73.png) ⇒
⇒![\arrb{ \b e_{\clr[gr]{x}} & A_y B_z - A_{\clr[gr]{z}} B_{\clr[gr]{y}} \\ \b e_{ y } & A_z B_x - A_{ x } B_{ z } \\ \b e_{ z } & A_x B_y - A_{ y } B_{ x } } $$ \arrb{ \b e_{\clr[gr]{x}} & A_y B_z - A_{\clr[gr]{z}} B_{\clr[gr]{y}} \\ \b e_{ y } & A_z B_x - A_{ x } B_{ z } \\ \b e_{ z } & A_x B_y - A_{ y } B_{ x } } $$](./eq/eq-ni-3f1914e954e791b937007adaf0bab189.png)



内積は外積と手順が同じのため、結果だけを示す。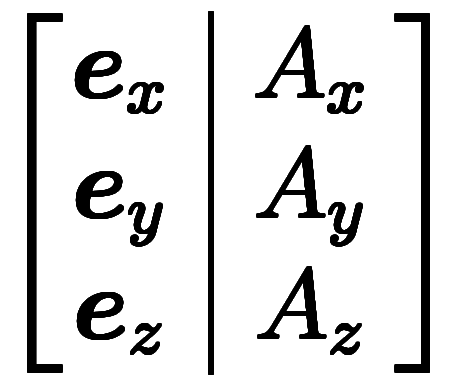
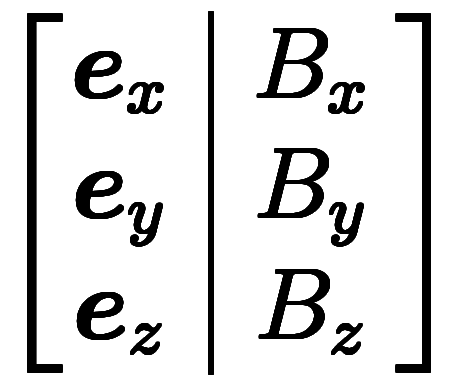 =
=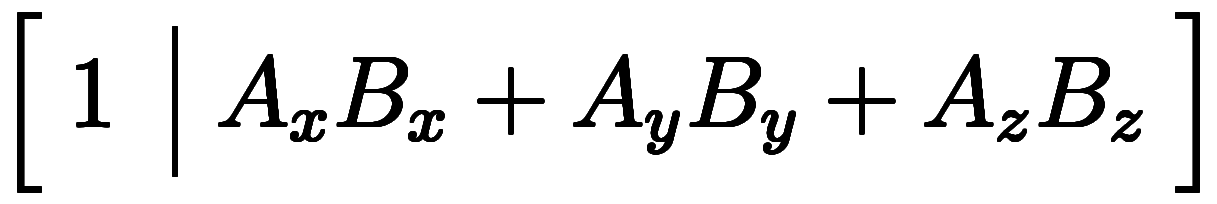

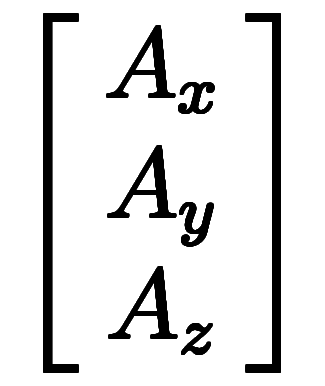
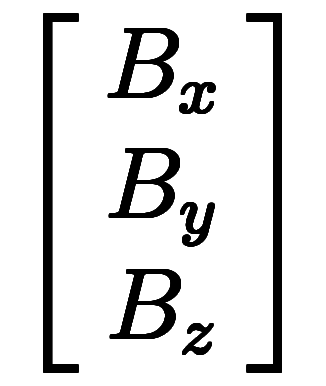 =
=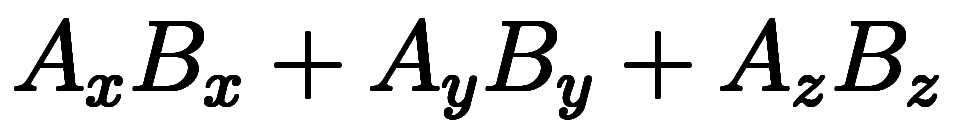



微分基底の乗算はウェッジ積と呼ばれる拡張された外積に統一されるている。普通はウェッジ記号「 」で常に表記されるが、猫式では互換性を考え、省略可能とする。代わりに、微分基底間の乗算は常に外積規則が適応され、交換不可とする。
」で常に表記されるが、猫式では互換性を考え、省略可能とする。代わりに、微分基底間の乗算は常に外積規則が適応され、交換不可とする。
手順は幾何基底の外積演算と全く同じのため、結果のみを示す。
 0次形式
0次形式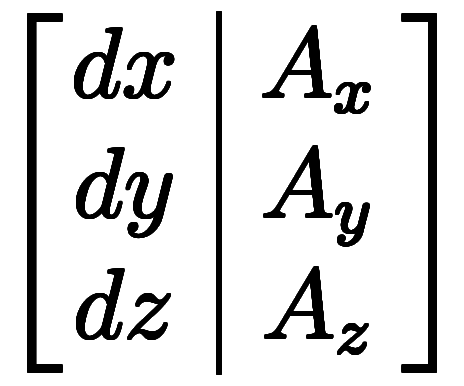

 =
=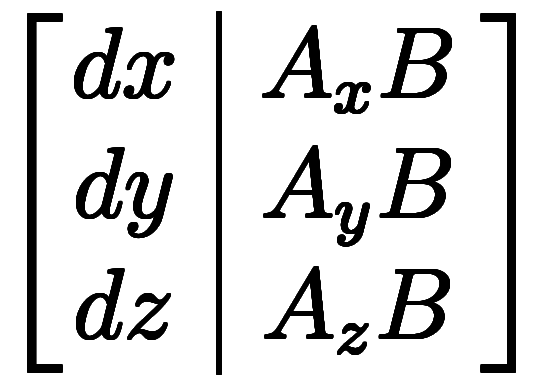
 1次形式
1次形式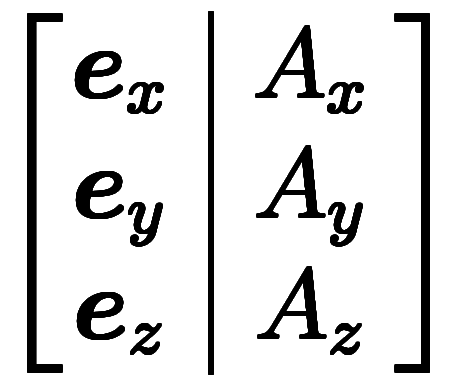

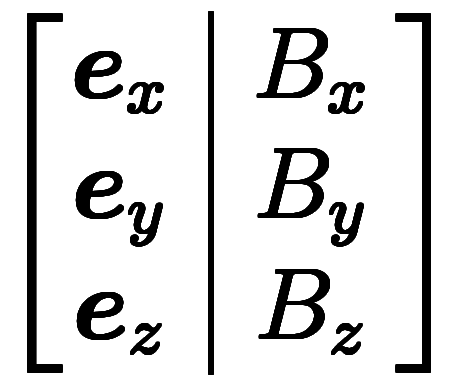 =
=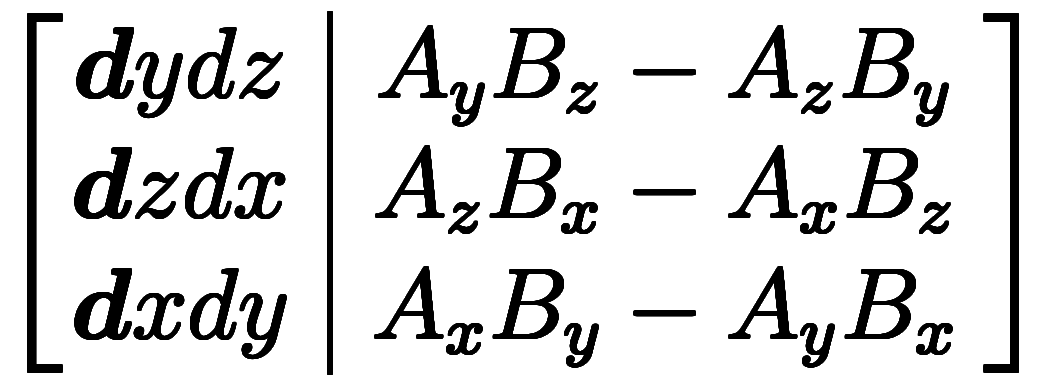
 2次形式
2次形式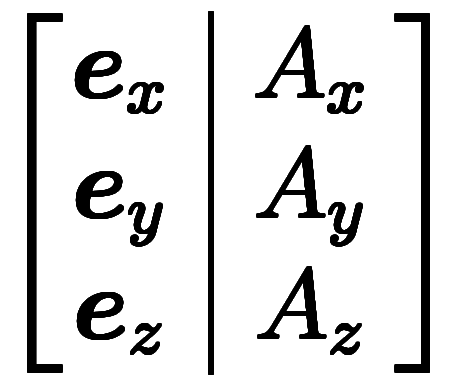

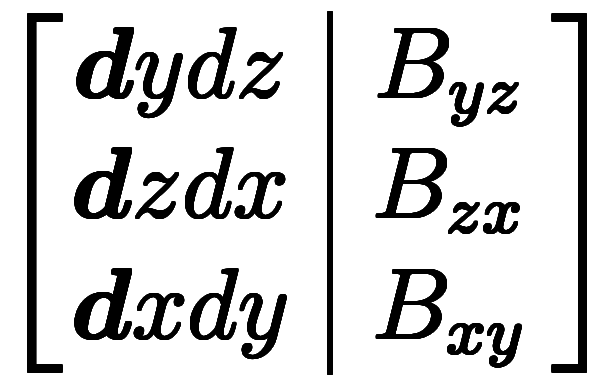 =
=



ベクトル積分演算子のところで、微小量に対する計算では減算項を抜くインチキ規則を導入した。実は、その意味は1次形式  1次形式の右辺にある。注目すべき点は、基底側と成分側の非対称性である。
1次形式の右辺にある。注目すべき点は、基底側と成分側の非対称性である。
まず、成分側は幾何基底の外積の成分側と一致する。このため、通常のベクトル計算は成分側の計算と言える。次ぎに、基底側には減算項が無く、成分側の計算と異なっている。通常のベクトル計算をしようとしても、微分基底が成分側になく、別の計算となっているため、当然失敗する。
一方で、加算項と基底は常に対応しているため、成分側として計算した結果から減算項を消すだけで、基底側の計算になる。後付けではあるが、これがインチキ規則の真の意味である。
また、倍積と内積の演算には元から減算項が現れないため、インチキするまでもない。したがって、通常のベクトル演算で上手く処理できないのは微分基底間の外積のみと言える。



……



……



……
 、
、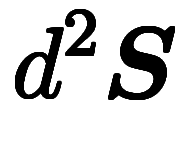 、
、 がそれぞれ、微分形式の1次形式、2次形式、3次形式の微分基底に対応している。1、2、3と並んだら、0を考えるのが猫式。線積分、面積分、体積分も同様、線、面、体と並んだら、点を考えるべし。というわけで、次回、
がそれぞれ、微分形式の1次形式、2次形式、3次形式の微分基底に対応している。1、2、3と並んだら、0を考えるのが猫式。線積分、面積分、体積分も同様、線、面、体と並んだら、点を考えるべし。というわけで、次回、 ──「点積分」。
──「点積分」。