加法定理 EditToHeaderToFooter

加法定理は、加減算の三角関数を三角関数の積に分解する公式。

三角関数は指数関数の仲間であり、加法定理は指数法則の１つに相当する。三角関数が$$ \csin $$か$$ \ccos $$のどちらかで未定であることを$$ \ctri $$と表記すると、加法定理を指数法則と似た形で書ける：

指数法則： $$ \exp(\alpha + \beta) = \exp(\alpha) \, \exp(\beta) $$

$$ (e^{\alpha + \beta} = e^\alpha \, e^\beta) $$

加法定理： $$ \spc{\ctri}{\exp}(\alpha \pm \beta) $$$$ \Rightarrow $$$$ \spc{\ctri}{\!\exp}(\alpha) \, \spc{\ctri}{\exp}(\beta) $$

要は、加法が乗法になるのが$$ \csin $$と$$ \ccos $$*1。

等号ではないのは、符号や係数、定数項などを省略しているため。そこで、式の左辺がそれぞれ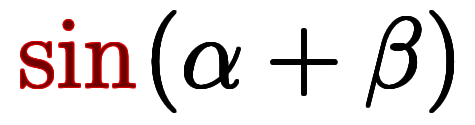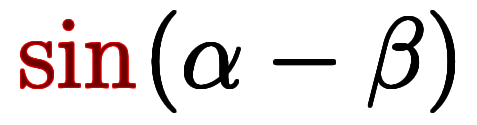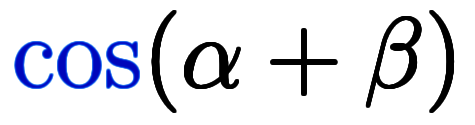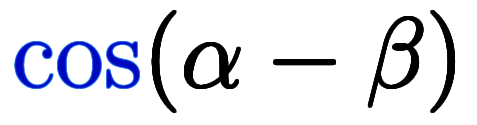$$ \csin(\alpha + \beta) $$、$$ \csin(\alpha - \beta) $$、$$ \ccos(\alpha + \beta) $$、$$ \ccos(\alpha - \beta) $$の場合について、等号が成立するように右辺を決めて行くのが組立の仕事。

*1 三角公式なんかよりこのような性質を覚える方が遥かに重要

1. 正弦合わせ

組立は$$ \ctri $$の決定から始める。三角関数は三角公式の骨組みのようなもので、これが決まらないと何も決まらない。

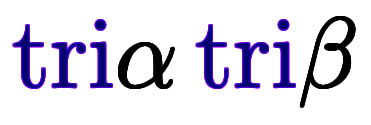猫式では、個々の項に対し、乗算している$$ \csin $$の数をその項の正弦数と定義する。加法定理の右辺にある$$ \ctri \alpha \, \ctri \beta $$には未定表記が2つあるため、組み合せは2×2＝4通り。それぞれの正弦数は次のようになる：

$$ \ccos \alpha $$$$ \ccos \beta $$ ── ０個 ── 偶数
$$ \csin \alpha $$$$ \ccos \beta $$ ── １個 ── 奇数
$$ \ccos \alpha $$$$ \csin \beta $$ ── １個 ── 奇数
$$ \csin \alpha $$$$ \csin \beta $$ ── ２個 ── 偶数

正弦数に関して次の組立規則が成り立つ：

正弦陰性則： $$ \csin $$が２つ掛け合わせる毎に、項の前に「$$ \iro[ak]- $$」が１つ増える

正弦奇偶則： 等式の各項において、正弦数は「全て奇数」または「全て偶数」

これらは猫式組立の真髄である。説明するには、大学で習う知識が必要になるため、後回し。ともかく、これらの規則を適応すると、負号が１つ現れ、右辺はそれぞれ２組ずつ絞られる：

$$ \csin(\alpha \pm \beta) $$ ── 奇数 ── $$ \csin \alpha $$$$ \ccos \beta $$、$$ \phantom-\! $$$$ \ccos \alpha $$$$ \csin \beta $$
$$ \ccos(\alpha \pm \beta) $$ ── 偶数 ── $$ \ccos \alpha $$$$ \ccos \beta $$、$$ \iro[ak]-\! $$$$ \csin \alpha $$$$ \csin \beta $$

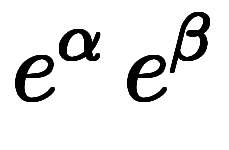これは、指数法則では$$ e $$しかないため、右辺は$$ e^\alpha \, e^\beta $$の１通りに決まるが、三角関数の場合は$$ \csin $$と$$ \ccos $$があるため、組合せは１通りに決まらないと考える程度で良い。

問題は２組の候補から左辺に来るべき１つの値を作り出す方法である。結論から言えば、単純に加算で繋げて積和形にすれば良い*2。ここまでの作業で次の形になる：

$$ \csin(\alpha \pm \beta) $$$$ \Rightarrow $$$$ \csin \alpha $$$$ \ccos \beta $$$$ + $$$$ \ccos \alpha $$$$ \csin \beta $$
$$ \ccos(\alpha \pm \beta) $$$$ \Rightarrow $$$$ \ccos \alpha $$$$ \ccos \beta $$$$ \iro[ak]- $$$$ \csin \alpha $$$$ \csin \beta $$

*2 和積公式でも同じ状況になるが積和形にはしない。それとの区別には補足を参考。

2. 符号合わせ

続けて、式に残る符号を決める。一般に、数式では「$$ + $$」が普通であり、「$$ \iro[ak]- $$」になるには理由が必要。実は、加法定理の中、左辺に減算の無い次の２式は既に出来上がっている。

$$ \csin(\alpha + \beta) $$$$ \Rightarrow $$$$ \csin \alpha $$$$ \ccos \beta $$$$ + $$$$ \ccos \alpha $$$$ \csin \beta $$
$$ \ccos(\alpha + \beta) $$$$ \Rightarrow $$$$ \ccos \alpha $$$$ \ccos \beta $$$$ - $$$$ \csin \alpha $$$$ \csin \beta $$

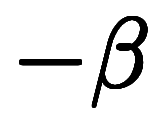残りの２式では、$$ \beta $$の符号が「$$ \iro[ak]- $$」に反転するため、右辺でも符号反転が起こる。結果的に、右辺でも$$ \beta $$を$$ -\beta $$に置き換えて、符号を計算することになるが、計算をしない猫式では次の簡易方法を用いる：

三角公式では、$$ \ccos $$が$$ \ccos(\iro[ak]- \beta) $$$$ = $$$$ \ccos(\beta) $$と符号を消すのを除き、他は全て$$ \csin(\iro[ak]- \beta) $$$$ = $$$$ \iro[ak]- \csin(\beta) $$のように符号を通す。このため、右辺は$$ \ccos \beta $$のみを見つけ、見つからなければ符号反転させれば良い。

以上の結果、加法定理の４式は次のようになる。

$$ \csin(\alpha \clr[ai]+ \beta) $$$$ = $$$$ \csin \alpha $$$$ \ccos \beta $$$$ \clr[ai]+ $$$$ \ccos \alpha $$$$ \csin \beta $$
$$ \csin(\alpha \clr[ak]- \beta) $$$$ = $$$$ \csin \alpha $$$$ \ccos \beta $$$$ \clr[ak]- $$$$ \ccos \alpha $$$$ \csin \beta $$
$$ \ccos(\alpha \clr[ai]+ \beta) $$$$ = $$$$ \ccos \alpha $$$$ \ccos \beta $$$$ \clr[ak]- $$$$ \csin \alpha $$$$ \csin \beta $$
$$ \ccos(\alpha \clr[ak]- \beta) $$$$ = $$$$ \ccos \alpha $$$$ \ccos \beta $$$$ \clr[ak]+ $$$$ \csin \alpha $$$$ \csin \beta $$

つづき ── 倍角公式? EditToHeaderToFooter
    初基 一覧 検索 最新 バックアップ リンク元   ヘルプ   最終更新のRSS