![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/三角公式/虚数正弦 のバックアップ(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/三角公式/虚数正弦 のバックアップ(No.3) |
虚数正弦 |
|
これらを使えば全ての三角公式を導ける。例えば、加法定理は次のように導ける:
| |
| オイラーの公式 |
| 指数法則 |
| オイラーの公式 |
| 乗算分配則 |
| 実部と虚部の分離 |
実部と虚部を別々に比較して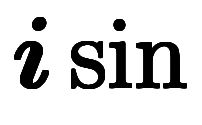 版の加法定理を得る:
版の加法定理を得る:
|
|
さらに虚数単位を計算して、通常の加法定理を得る:
|
|
表面的ではあるが、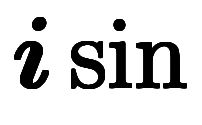 版の方では全て
版の方では全て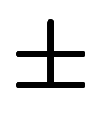 に統一しているのに対し、通常版では
に統一しているのに対し、通常版では の中に
の中に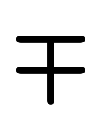 が1つだけ混ざっている。問題は、そこに複素数の計算規則があって、
が1つだけ混ざっている。問題は、そこに複素数の計算規則があって、 は
は の計算結果である。さらに、
の計算結果である。さらに、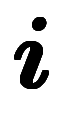 と
と は一緒に動くため、
は一緒に動くため、 があるところは必ず
があるところは必ず があり、「
があり、「 」が付く。よって、次の法則が成り立つ:
」が付く。よって、次の法則が成り立つ:
正弦奇偶則: 正弦数は、等式の各項を通して「全て奇数」または「全て偶数」 |
次に、通常の三角公式は全て実数である。複素数の式が実数の式になるには、「全ての項が純虚数」または「全ての項が実数」を満たす必要がある。純虚数の項では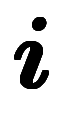 の数は奇数、実数の項では
の数は奇数、実数の項では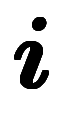 の数は偶数になる。これに加え、
の数は偶数になる。これに加え、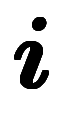 と
と は一緒に動くため、
は一緒に動くため、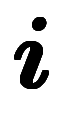 に対して言えることは、
に対して言えることは、 の数に対しても同じことが言えて、次の法則が成り立つ:
の数に対しても同じことが言えて、次の法則が成り立つ:
正弦陰性則: |



名前の問題。従来の余弦 や正弦
や正弦 と区別のため、猫式では
と区別のため、猫式では を実弦、
を実弦、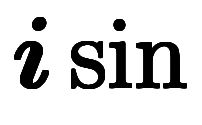 を虚弦と呼ぶ。
を虚弦と呼ぶ。
本質の問題。図1に示すように、余弦と正弦は、二次元平面上で考えようが、複素数平面上で考えようが、実数値の座標値に過ぎない。一方、図2に示すように、猫式の実弦と虚弦は座標値ではなく、複素数値である。