![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/点積分 のバックアップ(No.1) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
猫式/点積分 のバックアップ(No.1) |
点積分 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 猫式ベクトル積分表記 | 微小要素 | 対応する微分形式 | |
|---|---|---|---|
| 点積分 | ![\clr[bl]{\inte[P] d^{-0} f \, d^{0} p} $$ \clr[bl]{\inte[P] d^{-0} f \, d^{0} p} $$](./eq/eq-ni-8498b7499dac4372a4f5cebcda39cbfc.png) | 点要素 | 0次形式: |
| 線積分 | ![\inte[R] d^{-1} \b f \sx d^{1}\b r $$ \inte[R] d^{-1} \b f \sx d^{1}\b r $$](./eq/eq-ni-885981c73fbde7b1caddea7d2fa25406.png) | 線要素 | 1次形式: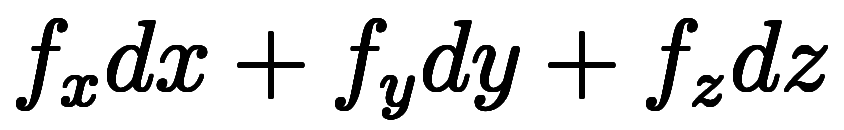 |
| 面積分 | ![\inte[S] d^{-2} \b f \sx d^{2}\b S $$ \inte[S] d^{-2} \b f \sx d^{2}\b S $$](./eq/eq-ni-a1849aeb4e4488161f56fe71b589ecd9.png) | 面要素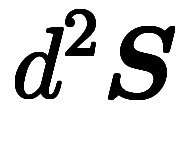 | 2次形式: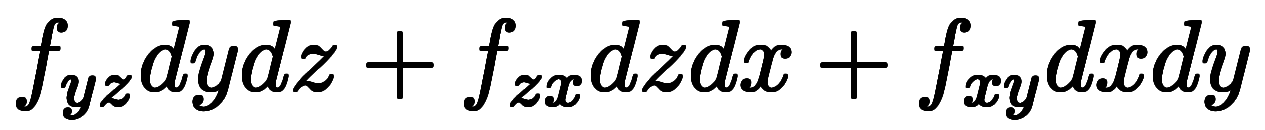 |
| 体積分 | ![\inte[V] d^{-3} f \, d^{3} V $$ \inte[V] d^{-3} f \, d^{3} V $$](./eq/eq-ni-6286457538502db0b53d18a8af996396.png) | 体要素 | 3次形式: |
数字は3、2、1、0で類推できるが、 、
、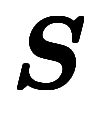 、
、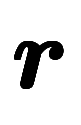 の次と言われても予測不能ので、とりあえず「点」→「point」→「p」のセンスで仮置き。
の次と言われても予測不能ので、とりあえず「点」→「point」→「p」のセンスで仮置き。
猫式で積分の回数を表す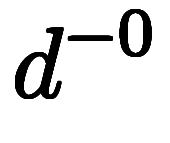 が
が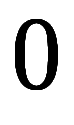 なのは積分が無いため、点積分は名ばかりで、実際の計算では積分は無いのが分かる。これは累次積分で計算するときの積分回数や、対応する微分形式からも類推可能。
なのは積分が無いため、点積分は名ばかりで、実際の計算では積分は無いのが分かる。これは累次積分で計算するときの積分回数や、対応する微分形式からも類推可能。
今回のポイントは、![\inte[P] d^{-0} f \, d^{0} p $$ \inte[P] d^{-0} f \, d^{0} p $$](./eq/eq-ni-7f0a6e4b6f98854a4e1183e843dac761.png) から
から と
と が消えても、
が消えても、![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png)
 が残る。猫式では、
が残る。猫式では、 は範囲指定の専用記号。
は範囲指定の専用記号。![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png)
 は範囲
は範囲 における
における の値と読める。例えば、
の値と読める。例えば、 は点
は点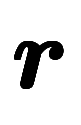 =
=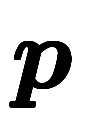 とすると、
とすると、![\inte[P] f(\b r) $$ \inte[P] f(\b r) $$](./eq/eq-ni-909c22dd0ce4fd57fab271fefe98ad12.png) =
=![\inte[p] f(\b r) $$ \inte[p] f(\b r) $$](./eq/eq-ni-ea524876606c39fb557b564088472273.png) =
= 。つまり、点積分は代入演算と等価。
。つまり、点積分は代入演算と等価。
![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) の意味
の意味 


3次元のベクトル置換積分定理には、線積分と面積分を結ぶストークスの定理、面積分と体積分を結ぶガウスの定理がある。点積分を考えば、点積分と線積分を結ぶ定理もあるはず。実際、以下の類推で形式的に式を作り出すと、それが積分の基本定理のベクトル版に見える。
| 系統名 | 略称 | 慣用名 | 猫式表記 |
|---|---|---|---|
| 点線置換積分 | 点線置換 | 積分の基本定理 | ![\clr[bl]{\inte[P] d^{-0} f \sx d^{0} p = \inte[R] d^{-1} \ddd{ f}{\b r} \sx d^{1}\b r} $$ \clr[bl]{\inte[P] d^{-0} f \sx d^{0} p = \inte[R] d^{-1} \ddd{ f}{\b r} \sx d^{1}\b r} $$](./eq/eq-ni-630087ea5fc990914936555f8b844a3e.png) |
| 線面置換積分 | 線面置換 | ストークスの定理 | ![\inte[R] d^{-1} \b f \sx d^{1}\b r = \inte[S] d^{-2} \ddd{\vx \b f}{\b r} \sx d^{2}\b S $$ \inte[R] d^{-1} \b f \sx d^{1}\b r = \inte[S] d^{-2} \ddd{\vx \b f}{\b r} \sx d^{2}\b S $$](./eq/eq-ni-34c622df05d7eb684a5b403afdab291d.png) |
| 面体置換積分 | 面体置換 | ガウスの定理 | ![\inte[S] d^{-2} \b f \sx d^{2}\b S = \inte[V] d^{-3} \ddd{\sx \b f}{\b r} \sx d^{3} V $$ \inte[S] d^{-2} \b f \sx d^{2}\b S = \inte[V] d^{-3} \ddd{\sx \b f}{\b r} \sx d^{3} V $$](./eq/eq-ni-6d3affc74a3feb1613f146105818c02a.png) |
積分の基本定理とは、1次元で![\inte[a]^b\! \ddd{f(r)}{r} dr $$ \inte[a]^b\! \ddd{f(r)}{r} dr $$](./eq/eq-ni-231a8597c1194b78addff52748373fd1.png) =
=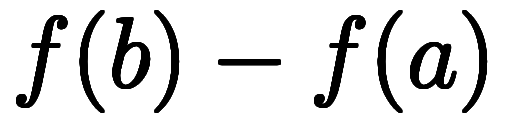 。ベクトル場では、
。ベクトル場では、![\inte[\b a]^{\b b}\! \ddd{f(\b r)}{\b r} \sx d\b r $$ \inte[\b a]^{\b b}\! \ddd{f(\b r)}{\b r} \sx d\b r $$](./eq/eq-ni-d6b72a95fa2e73e18924d70419167024.png) =
= 。点積分を使えば、大雑把に
。点積分を使えば、大雑把に![\inte[\b a]^{\b b}\! d^- \ddd{f(\b r)}{\b r} d\b r $$ \inte[\b a]^{\b b}\! d^- \ddd{f(\b r)}{\b r} d\b r $$](./eq/eq-ni-e8ddce8c71aa881bfa21969b2c5ea62d.png) =
=![\inte[\b a]^{\b b}\! f(\b r) $$ \inte[\b a]^{\b b}\! f(\b r) $$](./eq/eq-ni-24e81edbc6684477a0290ece862b1656.png) 。
。
厳密には、線積分の![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は
は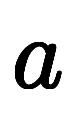 から
から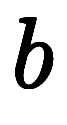 までの区間
までの区間![\inte[R] $$ \inte[R] $$](./eq/eq-ni-36407cd8870cb013ab519e692d6f8e33.png) 、点積分の
、点積分の![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は
は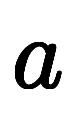 と
と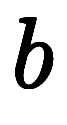 の2点
の2点![\inte[P] $$ \inte[P] $$](./eq/eq-ni-2ab83b26f02d30bea1a1a8b5fdac4b8a.png) と意味が微妙に異なる。猫式では、区別するため、次のように線積分を不定積分と点積分に分けて考え、
と意味が微妙に異なる。猫式では、区別するため、次のように線積分を不定積分と点積分に分けて考え、![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は常に点の範囲指定と読む。
は常に点の範囲指定と読む。
| | 左側は猫式、右側は対応する通常表記 |
= | = | 線積分を不定積分と点積分に分離 |
= | = | 不定積分実行 |
= | = | 点積分実行 |
この解釈では、![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は定積分の
は定積分の![\left[ \fracstrut \cdots \right]_b^a $$ \left[ \fracstrut \cdots \right]_b^a $$](./eq/eq-ni-c5a76d639d93701aa320abd23ea70aba.png) と等価になる。一般に、線積分の被積分関数が
と等価になる。一般に、線積分の被積分関数が と書けない限り*1、積分値は経路に依存し、2つの端点だけでは決まらない。このためにも、1次元という特殊な場合でも、
と書けない限り*1、積分値は経路に依存し、2つの端点だけでは決まらない。このためにも、1次元という特殊な場合でも、![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は端から端点の表現であって、区間ではないと考えた方が良い。
は端から端点の表現であって、区間ではないと考えた方が良い。



上記3つの公式を基底成分表記で書くと次のようになる。
| 低階側 | 高階側 | |||
|---|---|---|---|---|
| 点線置換 | ![\inte[P] d^{-1} \arrb{ d^0 p & f } $$ \inte[P] d^{-1} \arrb{ d^0 p & f } $$](./eq/eq-ni-305fe28fc34518d2a934ad2632e47f84.png) | =![\inte[R] d^{-1} \arrb{d\b r & \ddd{}{\b r}} \wx \arrb{ d^0 p & f } $$ \inte[R] d^{-1} \arrb{d\b r & \ddd{}{\b r}} \wx \arrb{ d^0 p & f } $$](./eq/eq-ni-b273a329db8669de43e0813a7bb80425.png) | =![\inte[R] d^{-1} \arrb{d\b r \wx d^0 p & \ddd{}{\b r} f } $$ \inte[R] d^{-1} \arrb{d\b r \wx d^0 p & \ddd{}{\b r} f } $$](./eq/eq-ni-5cd3142365430be6b0ab97a461cc93d1.png) | =![\inte[R] d^{-0} \arrb{d^1\b r & \ddd{}{\b r} f } $$ \inte[R] d^{-0} \arrb{d^1\b r & \ddd{}{\b r} f } $$](./eq/eq-ni-29a690435b94bd7a8b6c94480c4312ec.png) |
| 線面置換 | ![\inte[R] d^{-2} \arrb{ d^1\b r & \b f } $$ \inte[R] d^{-2} \arrb{ d^1\b r & \b f } $$](./eq/eq-ni-02f34c6222a68683ea1da20361023e7f.png) | =![\inte[S] d^{-2} \arrb{d\b r & \ddd{}{\b r}} \wx \arrb{ d^1\b r & \b f } $$ \inte[S] d^{-2} \arrb{d\b r & \ddd{}{\b r}} \wx \arrb{ d^1\b r & \b f } $$](./eq/eq-ni-d4a5243a382d1655c616bcc10cb105ae.png) | =![\inte[S] d^{-2} \arrb{d\b r \wx d^1\b r & \ddd{}{\b r} \vx \b f } $$ \inte[S] d^{-2} \arrb{d\b r \wx d^1\b r & \ddd{}{\b r} \vx \b f } $$](./eq/eq-ni-7289be3005fc3560df4ebb7cd311fa1b.png) | =![\inte[S] d^{-1} \arrb{d^2\b S & \ddd{}{\b r} \vx \b f } $$ \inte[S] d^{-1} \arrb{d^2\b S & \ddd{}{\b r} \vx \b f } $$](./eq/eq-ni-7bb9eb328619764e36390059e86600c9.png) |
| 面体置換 | ![\inte[S] d^{-3} \arrb{ d^2\b S & \b f } $$ \inte[S] d^{-3} \arrb{ d^2\b S & \b f } $$](./eq/eq-ni-a33ecd7944fc3f48c9638aa9c067deb5.png) | =![\inte[V] d^{-3} \arrb{d\b r & \ddd{}{\b r}} \wx \arrb{ d^2\b S & \b f } $$ \inte[V] d^{-3} \arrb{d\b r & \ddd{}{\b r}} \wx \arrb{ d^2\b S & \b f } $$](./eq/eq-ni-b8bd6aa26bace540c22aa9a93d62725e.png) | =![\inte[V] d^{-3} \arrb{d\b r \wx d^2\b S & \ddd{}{\b r} \sx \b f } $$ \inte[V] d^{-3} \arrb{d\b r \wx d^2\b S & \ddd{}{\b r} \sx \b f } $$](./eq/eq-ni-606affc78667c203aaeb461f09496400.png) | =![\inte[V] d^{-2} \arrb{d^3 V & \ddd{}{\b r} \sx \b f } $$ \inte[V] d^{-2} \arrb{d^3 V & \ddd{}{\b r} \sx \b f } $$](./eq/eq-ni-f1416c82964be2a61c2bdf3764d7533c.png) |
左から右は、積分階数の低い式から高い式までの変形。まずは、外微分 を挿入する。基底と成分の分母が打消し、成分の分子
を挿入する。基底と成分の分母が打消し、成分の分子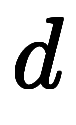 が残るため、ここで積分の階数が上がり、積分範囲も変わる。次ぎに、ウェッジ積の展開で、微小基底の階数に応じて、成分側が倍積、外積、内積に分かれる。ここで、3次元ベクトルの積演算が出揃うことからも、点線置換は誠の仲間であるのが分かる。
が残るため、ここで積分の階数が上がり、積分範囲も変わる。次ぎに、ウェッジ積の展開で、微小基底の階数に応じて、成分側が倍積、外積、内積に分かれる。ここで、3次元ベクトルの積演算が出揃うことからも、点線置換は誠の仲間であるのが分かる。



点積分を考えて初めて、3次元でのベクトル積分が点、線、面、体と揃う。これらを結ぶ置換積分が点線置換、線面置換、面体置換の3本セット。高校から使ってきた積分の基本定理は、点線置換の立場から眺めると![\inte[a]^b $$ \inte[a]^b $$](./eq/eq-ni-6acd562f3f50bde871ab6469e281cb41.png) は2通りの解釈が出来ることが分かる。
は2通りの解釈が出来ることが分かる。
基底成分表示で書いた場合、3式の共通点として の挿入とあるが、ここで猫式の発想、
の挿入とあるが、ここで猫式の発想、 が挿せれば
が挿せれば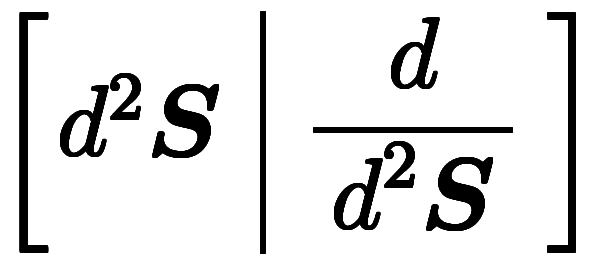 も挿せるはず。と言うわけで、次回「面微分」。
も挿せるはず。と言うわけで、次回「面微分」。