![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
線形演算子で繋がる特性方程式 |
背景 |
漸化式: |
|
|
特性方程式: |
|
|
等式変形: |
|
|
ここで、数列 

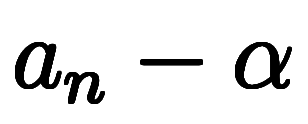 を考えば、初項
を考えば、初項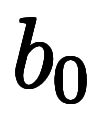

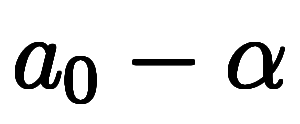 、公比
、公比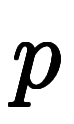 の数列のため、
の数列のため、
その一般項は、
|
 を移項すれば、
を移項すれば、 の一般項が求まる。
の一般項が求まる。
|



連続3項の漸化式として、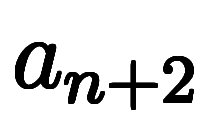

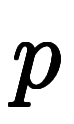
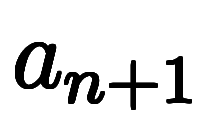

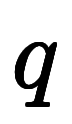


 のタイプの問題も高校で扱う。
のタイプの問題も高校で扱う。
解き方は、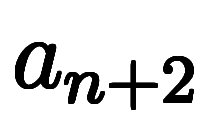 を
を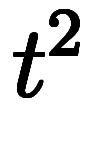 、
、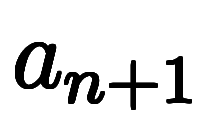 を
を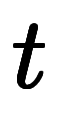 、
、 を
を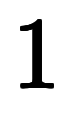 に差し替えた特性方程式
に差し替えた特性方程式 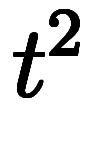

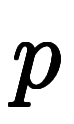
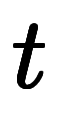

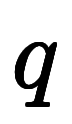

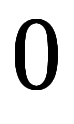 を解き、
を解き、
その解を と
と と置けば*6、特性方程式が
と置けば*6、特性方程式が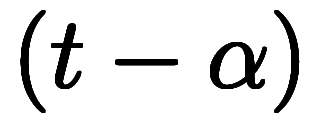
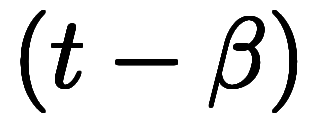

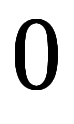 となる。
となる。
すると、解と係数の関係で 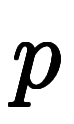




 、
、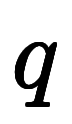


 と言えるので、これを利用して、
と言えるので、これを利用して、
漸化式を数列 と
と の式と、公比が
の式と、公比が の漸近式に分離した形に変形できる。
の漸近式に分離した形に変形できる。
|
|
|
同様に、 と
と が対称的なので、逆に扱った変換もできて、
が対称的なので、逆に扱った変換もできて、
|
それぞれから等比数列を出して、
|
|
さらに数列の差を取れば、
|
よって、
|






一般に微分可能な1変数関数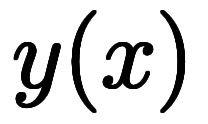 を
を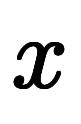 を
を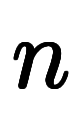 回微分した
回微分した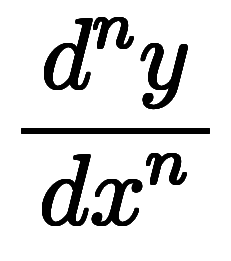 を全て
を全て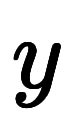 の常微分と言い、
の常微分と言い、
常微分の線形結合

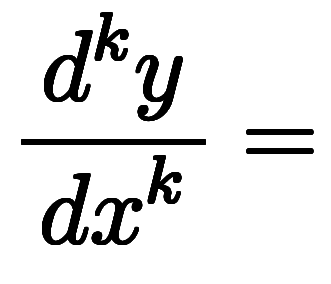
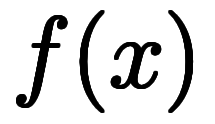 を線形常微分方程式と呼ぶ。
を線形常微分方程式と呼ぶ。
全ての が
が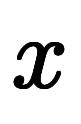 に対して定数である場合、定数係数線形常微分方程式と呼ぶ。
に対して定数である場合、定数係数線形常微分方程式と呼ぶ。
要は具体に、
1階定数係数線形常微分方程式は |
| |
2階定数係数線形常微分方程式は |
|
|
煩わしいので、一般的には を省き、最高階の係数を
を省き、最高階の係数を とし、微分演算子
とし、微分演算子

 を導入する。
を導入する。
1階定数係数線形常微分方程式: |
| |
2階定数係数線形常微分方程式: |
|
|



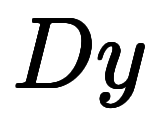


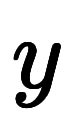

 は辺々に
は辺々に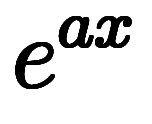 を掛けることで、単純な微分に変形できる。
を掛けることで、単純な微分に変形できる。
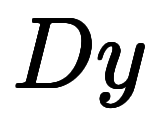




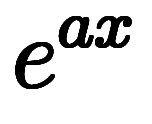 のため、
のため、
| |
| |
| |
| 積の微分 |
|
|
|
ここで、元の方程式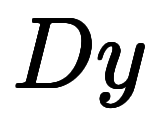



 は形式的に
は形式的に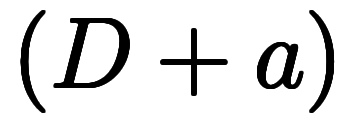
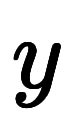

 と書けるので、
と書けるので、
以上の結果を以って、線形微分演算子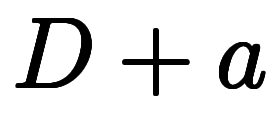 の逆演算子
の逆演算子 を定義できる。
を定義できる。
|



特性方程式を利用した標準的な解法は説明するのに大変な労力が要る*7*8。
一方で、凌宮数学では線形微分演算子 に分解する方法で簡単化ている*9。
に分解する方法で簡単化ている*9。
そのため、ここは楽して凌宮数学の解法を示す。
2階定数係数線形常微分方程式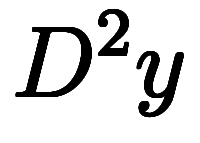


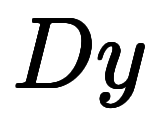

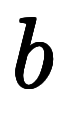
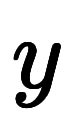

 に対し、
に対し、
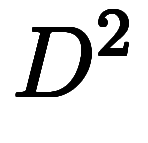




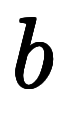
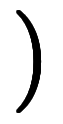
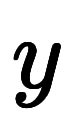

 に変形してから、
に変形してから、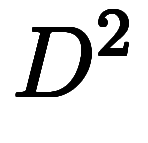 を
を 、
、 を
を 、
、 を
を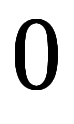 に差し替えた特性方程式を解く。
に差し替えた特性方程式を解く。
特性方程式




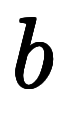

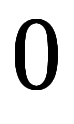 は二次方程式で、
は二次方程式で、
その解を と
と と置けば、以下の解と係数の関係が成り立つ。
と置けば、以下の解と係数の関係が成り立つ。
|
ただし、
|
|
この関係を使えば、2階の線形微分演算子を同様に1階線形微分演算子の合成に分解できる。
|
よって、
|
|
これを1階線形微分演算子の逆演算として解けば入れ子の積分になる。
あとは積分定数も忘れずに積分するだけで解ける*11。




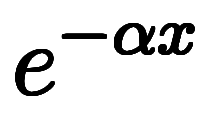


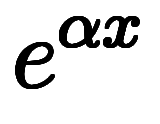

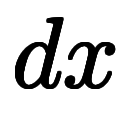

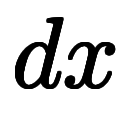
 のようになる。
のようになる。