![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
1階線形常微分演算子 のバックアップ(No.7) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
1階線形常微分演算子 のバックアップ(No.7) |
凌宮表記術: |
|
定数係数の高階線形常微分方程式を解くため、
微分演算子

 による演算子法が工学で多用される:
による演算子法が工学で多用される:
|
微分演算子 を使えば、微分方程式が簡潔になり、扱いやすくなる。
を使えば、微分方程式が簡潔になり、扱いやすくなる。
しかし、上記の通り、演算子法の要は合成された微分演算子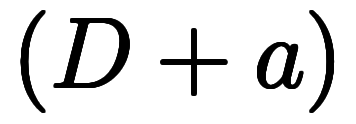 にある。
にある。
特に を計算する際、不定積分を意味する
を計算する際、不定積分を意味する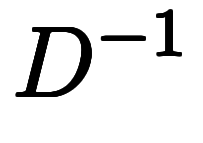 への変換が重要になる。
への変換が重要になる。
これに対し、凌宮数学では、 を纏めて1つの演算子として表記する:
を纏めて1つの演算子として表記する:
1階線形常微分演算子: |
1階線形常微分方程式: |
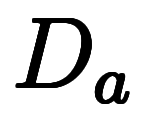 と
と

 の相互変換
の相互変換 








前述の通り、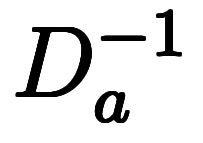 を計算するには、不定積分を意味する
を計算するには、不定積分を意味する![D_{\iro[ak]{0}}^{-1} $$ D_{\iro[ak]{0}}^{-1} $$](./eq/eq-ni-2e51dc54ac0dfdca3c3813141e70cf3a.png) に変換する必要がある。
に変換する必要がある。
幸い、その変換方法は、解の公式から簡単に分かる。
まず、

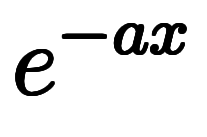



 に対し、
に対し、
不定積分を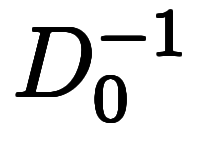 に直すと、
に直すと、


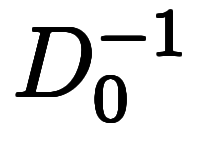

 が得られる。
が得られる。
これと、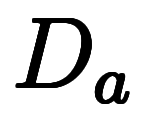 で記述される解
で記述される解

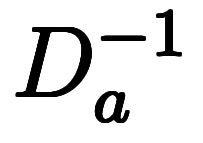
 と比較すれば、演算子の変換式が得られる:
と比較すれば、演算子の変換式が得られる:
|
この変換式は、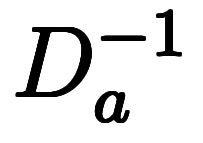 を
を 、
、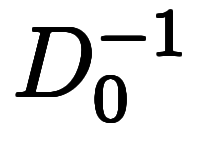 、
、 の3つの演算に分解しているように扱える。
の3つの演算に分解しているように扱える。
そこで、凌宮数学では、 を指数変換演算子として表記する:
を指数変換演算子として表記する:
|
一方で、 は自ずと
は自ずと を
を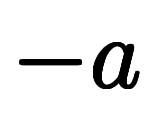 に置換した
に置換した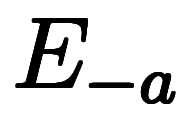 になる。
になる。
さらに、





 であるため、
であるため、 と
と が互いに逆演算である。
が互いに逆演算である。
|



未知関数 と既知関数
と既知関数 に着目すると、原方程式と解の公式はそれぞれ次のように捉えられる:
に着目すると、原方程式と解の公式はそれぞれ次のように捉えられる:
 に対し微分を含む操作を施すと既知関数
に対し微分を含む操作を施すと既知関数 が得られる
が得られる に対し微分を含む操作を施すと未知関数
に対し微分を含む操作を施すと未知関数 が得られる
が得られるそうすると、上記解答は次のように見える:
| |
| 原方程式 |
⇔ | 両辺に積分因子 |
⇔ | 積の微分に嵌める(不定積分を実行) |
⇔ | 1つの微分に纏める(部分積分を実行) |
⇔ | 積分する |
⇔ | 両辺に |
上記の解き方では、 と
と では単純な微分・積分の関係にならないため、
では単純な微分・積分の関係にならないため、
一旦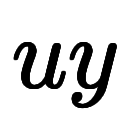

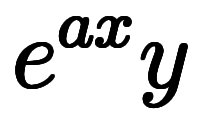 と
と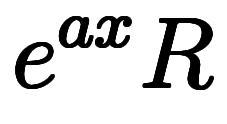 に変換してから、単純な微分を単純な積分に直している。
に変換してから、単純な微分を単純な積分に直している。
そういう意味で、解答例の最初と最後だけに着目すると、 と
と に関する一対の複雑な微分と積分にも見える:
に関する一対の複雑な微分と積分にも見える:




 が
が から
から への複雑な微分
への複雑な微分





 は
は から
から への複雑な積分
への複雑な積分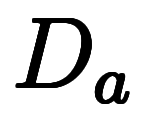 を
を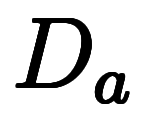






 と定義し、
と定義し、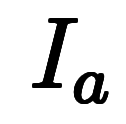 を
を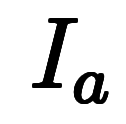






 と定義すると、
と定義すると、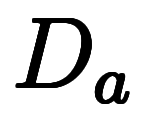
![\iro[gy]y $$ \iro[gy]y $$](./eq/eq-ni-48d32a2569f09f042196c7ad3e4b5898.png)

![\iro[gy]R $$ \iro[gy]R $$](./eq/eq-ni-2d930a54fd3cb219703755c888a54f90.png) ⇔
⇔ ![\iro[gy]y $$ \iro[gy]y $$](./eq/eq-ni-48d32a2569f09f042196c7ad3e4b5898.png)

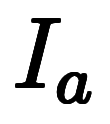
![\iro[gy]R $$ \iro[gy]R $$](./eq/eq-ni-2d930a54fd3cb219703755c888a54f90.png)
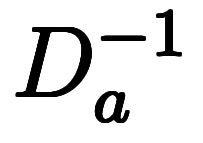

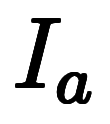





 と置きながら
と置きながら


 の解になるのが非論理的な面がある
の解になるのが非論理的な面がある