![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップの現在との差分(No.17) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップの現在との差分(No.17) |
凌宮読取術:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
オイラーの連鎖式: |
 などを約分して
などを約分して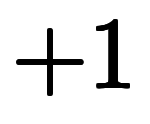 にしたどころで、そんな期待を裏切る
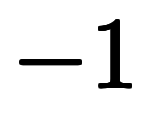
にしたどころで、そんな期待を裏切る![\iro[ao]-1 $$ \iro[ao]-1 $$](./eq/eq-ni-06be3155fba177d8741c844121a4ac2c.png) である。
である。 などを形式的に約分して
などを形式的に約分して と書きたいどころ、期待を裏切る
と書きたいどころ、期待を裏切る![\iro[ak]-1 $$ \iro[ak]-1 $$](./eq/eq-ni-b26c0f2a5c6ba49208b213c1e521f90d.png) である。
である。 が約分できる結果だけ見て、
が約分できる結果だけ見て、 を約分するから上手く行かない。
を約分するから上手く行かない。 が約分できる原因を考えば、
が約分できる原因を考えば、 を符号込みで約分できるようになる。
を符号込みで約分できるようになる。 が約分できる結果だけ見て
が約分できる結果だけ見て をそのまま消すから、計算が上手く行かない。
をそのまま消すから、計算が上手く行かない。 が約分できる仕組みを見て
が約分できる仕組みを見て を正しく読み替えると、約分も負号も直観的に考えられる。
を正しく読み替えると、約分も負号も直観的に考えられる。 |
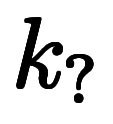 は全て係数であり、約分も符号も小学校同様に扱って良い。
は全て係数であり、約分も符号も小学校同様に扱って良い。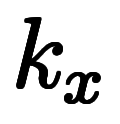 、
、 、
、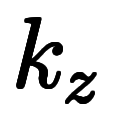 は全て普通の係数でしかないため、約分も符号処理も小学校レベルで済む。
は全て普通の係数でしかないため、約分も符号処理も小学校レベルで済む。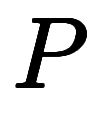 、体積
、体積 、温度
、温度 を結ぶマクスウェルの規則
を結ぶマクスウェルの規則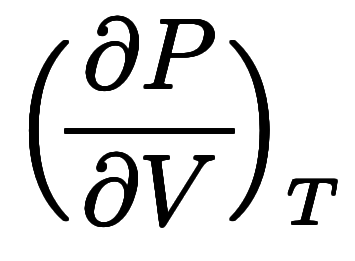
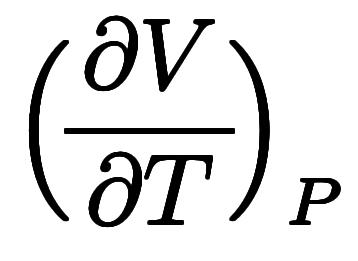
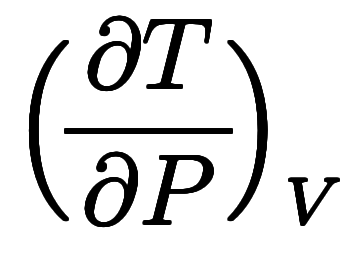

 の形で学ぶことになる。
の形で学ぶことになる。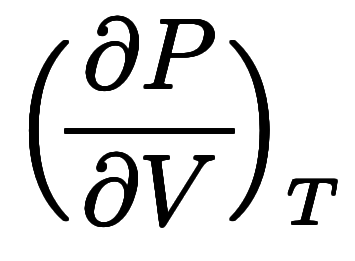
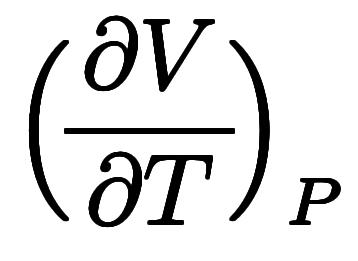
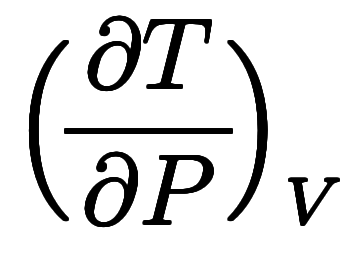

 の形で学ぶことになる。
の形で学ぶことになる。




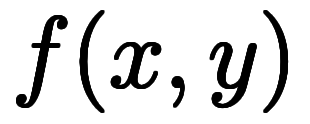 は1次式
は1次式

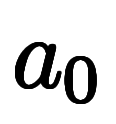

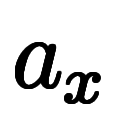


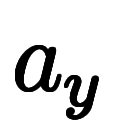
 と近似できるが、
と近似できるが、 と
と の係数
の係数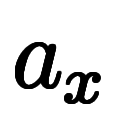 と
と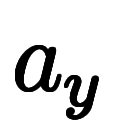 が微分係数で、それぞれが
が微分係数で、それぞれが の偏微分
の偏微分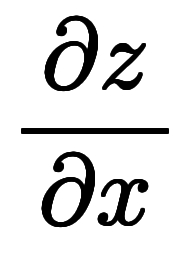 、
、 となる。
となる。

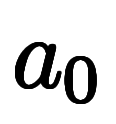

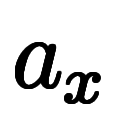


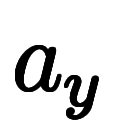
 から
から や
や につて解いた一次式からも微分係数が得られる。
につて解いた一次式からも微分係数が得られる。 について解いた式からは、
について解いた式からは、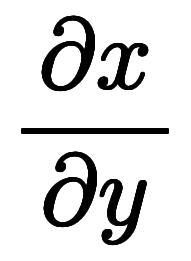 、
、 が得られる。
が得られる。 について解いた式からは、
について解いた式からは、 、
、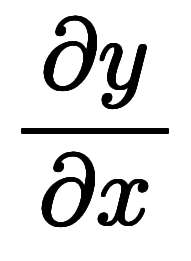 が得られる。
が得られる。



表1:   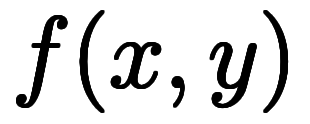 の1次近似と微分係数 の1次近似と微分係数 |
|---|
| 1次近似 | 微分係数 | 値 | ||
|---|---|---|---|---|
| 係数表記 | 関数表記 | 変数表記 |
|---|
  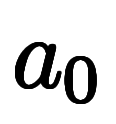  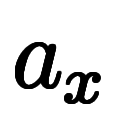   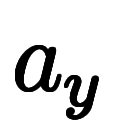  | 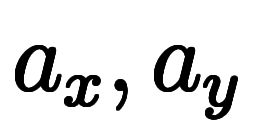 | 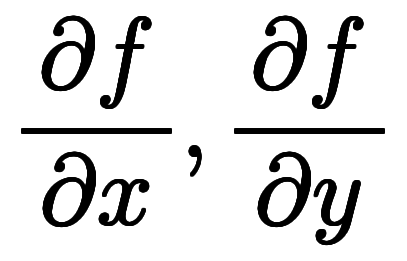 | 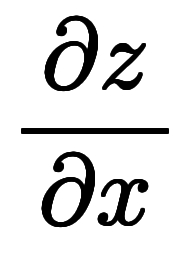   |    |
  ![\ffd{\iro[ak]-a_0}{a_x} $$ \ffd{\iro[ak]-a_0}{a_x} $$](./eq/eq-ni-386492f401adc6bff576e86994e118cb.png)  ![\ffd{\iro[ak]-a_y}{a_x} $$ \ffd{\iro[ak]-a_y}{a_x} $$](./eq/eq-ni-827c62a3875ee3982a8317a14d8574ff.png)     | ![\iro[hi]{b_y, b_z} $$ \iro[hi]{b_y, b_z} $$](./eq/eq-ni-5cd80dbb262d33c0e55b226c8155b3cf.png) | ![\iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$ \iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$](./eq/eq-ni-09dbcb84ed738563f857513f65e235a3.png) | 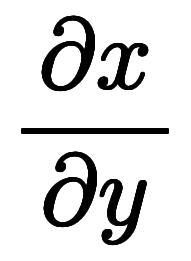   | ![\iro[ak]- \ffd{a_y}{a_x} $$ \iro[ak]- \ffd{a_y}{a_x} $$](./eq/eq-ni-de10df14b576084b352a48328f3d7dde.png)   |
  ![\ffd{\iro[ak]-a_0}{a_y} $$ \ffd{\iro[ak]-a_0}{a_y} $$](./eq/eq-ni-0306457dec638e0b90033523c1fe8826.png)     ![\ffd{\iro[ak]-a_x}{a_y} $$ \ffd{\iro[ak]-a_x}{a_y} $$](./eq/eq-ni-6b56887e798e5c3b6251fa1b4a5e9487.png)  | ![\iro[hi]{c_z, c_x} $$ \iro[hi]{c_z, c_x} $$](./eq/eq-ni-259b3c99b6e44740a99e8d3867b62ffb.png) | ![\iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$ \iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$](./eq/eq-ni-37204427fdbfa2bae56fe3a9b2a33042.png) |   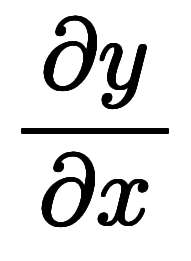 |   ![\iro[ak]- \ffd{a_x}{a_y} $$ \iro[ak]- \ffd{a_x}{a_y} $$](./eq/eq-ni-fceded1aba4e085139a06aa0134d4a3b.png) |
![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が発生することである。
」が発生することである。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」付くのは別の独立変数の項に限る。
」付くのは別の独立変数の項に限る。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を正しく書ける。
」を正しく書ける。| 被近似関数 | 1次近似 | 微分係数 | 値 | |||
|---|---|---|---|---|---|---|
| 記号 | 関数 | 従属変数 |
|---|
  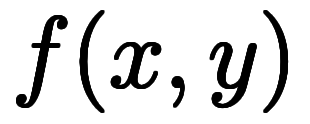 |   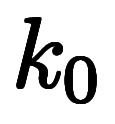  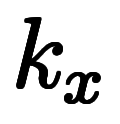     | 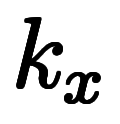   |    | 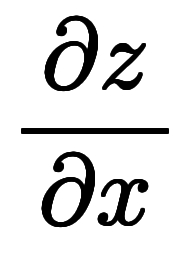   |    | |
  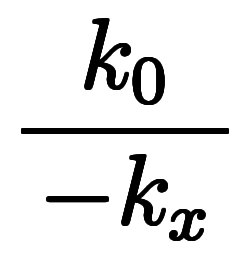     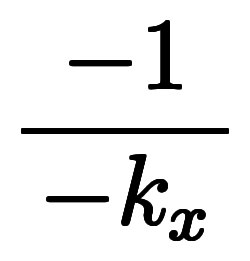  | 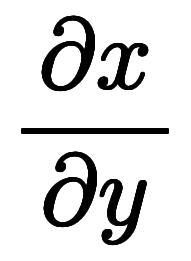   | ![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)    |
    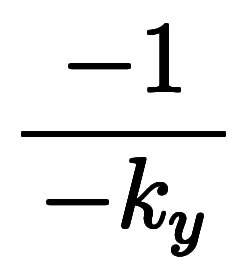     |   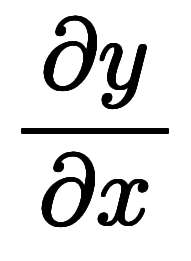 | 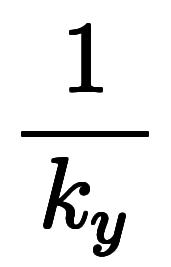  ![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)  |
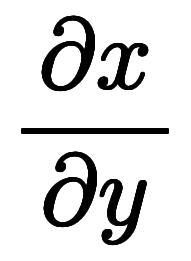 や
や を計算するのに、
を計算するのに、

 の1次近似式から移項で作った式を利用した。
の1次近似式から移項で作った式を利用した。

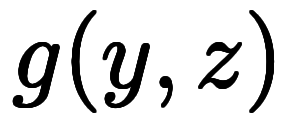 と置いて
と置いて




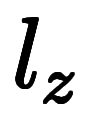
 と近似しても良いが、記号が増えるだけで計算にならん。
と近似しても良いが、記号が増えるだけで計算にならん。

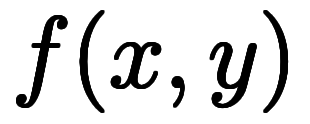 も
も

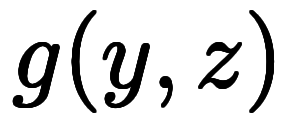 も同じ関係を記述している以上、近似式も1つ選んで使い続けば良い。
も同じ関係を記述している以上、近似式も1つ選んで使い続けば良い。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」の有無を判定できる。
」の有無を判定できる。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」有り
」有り![\iro[kr]- $$ \iro[kr]- $$](./eq/eq-ni-9b705174bef0f0403f453c5e8265c584.png) 」無し
」無し![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が生じること。
」が生じること。 にしていること。
にしていること。![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が残る。
」が残る。![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」を正しく扱えられる。
」を正しく扱えられる。






 への適応
への適応 





 は、陽関数
は、陽関数

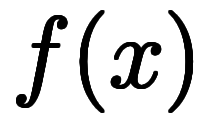 と陰関数
と陰関数

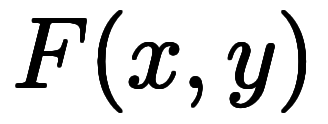 の2通りの考え方がある。
の2通りの考え方がある。![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が付く性質を持つ。
」が付く性質を持つ。

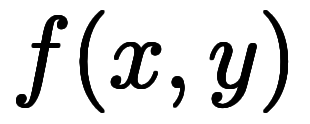 の例では、
の例では、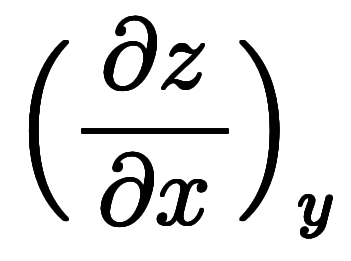 や
や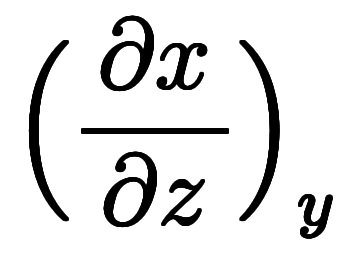 が陽微分になる。
が陽微分になる。

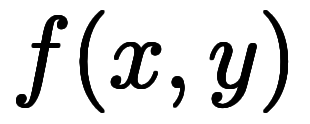 の例では、
の例では、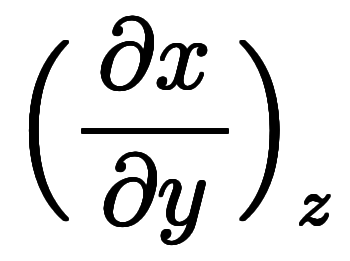 や
や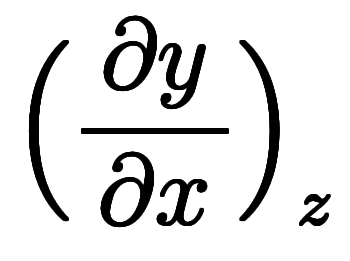 が陰微分になる。
が陰微分になる。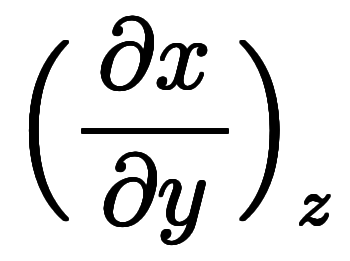 は
は を陰関数扱い *7にした陰微分になる。
を陰関数扱い *7にした陰微分になる。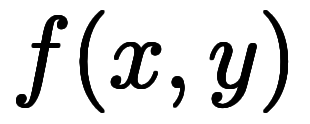 は一般的に
は一般的に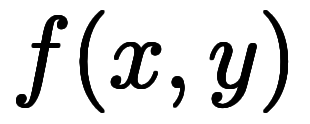




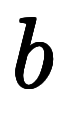


 で一次近似できる。
で一次近似できる。 と
と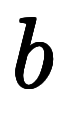 はそれぞれ
はそれぞれ と
と に対応する係数で、
に対応する係数で、 は定数項である。
は定数項である。 を
を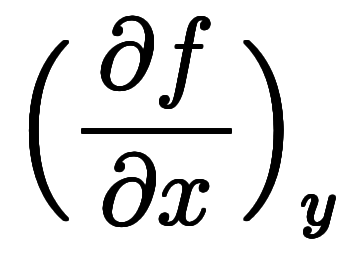 、
、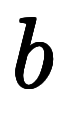 を
を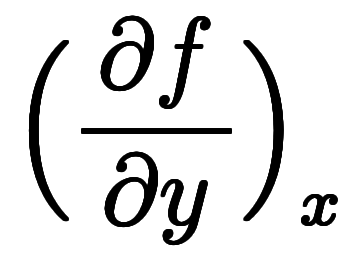 と書くのが微分係数としての微分である。
と書くのが微分係数としての微分である。

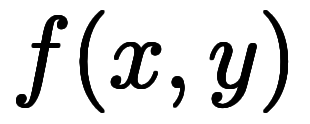 の一次近似が
の一次近似が




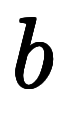


 になり、
になり、

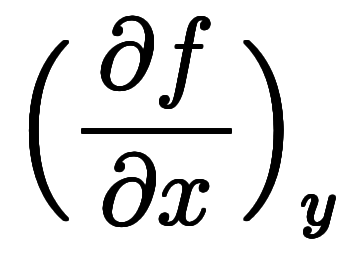

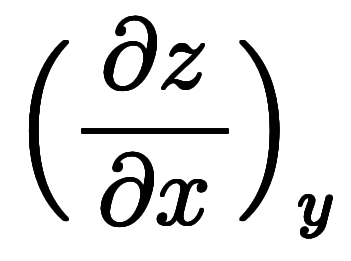 のように関数値の代わりに従属変数で書くことができる。
のように関数値の代わりに従属変数で書くことができる。




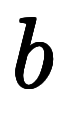


 を変形して求める必要がある。
を変形して求める必要がある。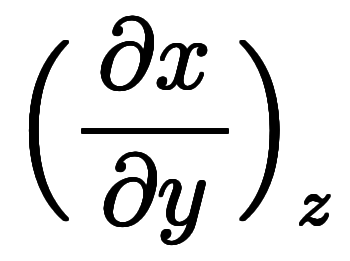 は
は

![\ffd{z}{a} \iro[ao]- \ffd{b}{a}y \iro[ao]- \ffd{k}{a} $$ \ffd{z}{a} \iro[ao]- \ffd{b}{a}y \iro[ao]- \ffd{k}{a} $$](./eq/eq-ni-c6aabdffd2dfaa077292fcea8e53f307.png) にしてから、
にしてから、  の係数を取って
の係数を取って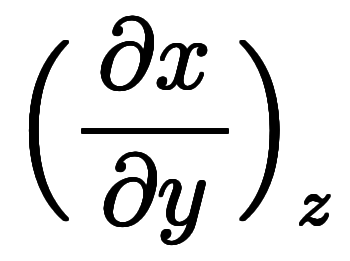

![\iro[ao]- \ffd{b}{a} $$ \iro[ao]- \ffd{b}{a} $$](./eq/eq-ni-0324a692c3a56fc3d4e25207e55cd20c.png) と求まる。
と求まる。![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が付いた値になる。
」が付いた値になる。![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が付く性質を持つ *8。
」が付く性質を持つ *8。



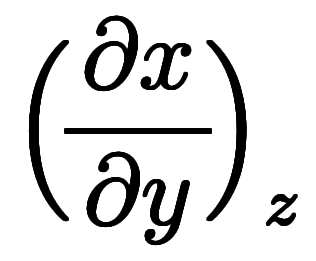
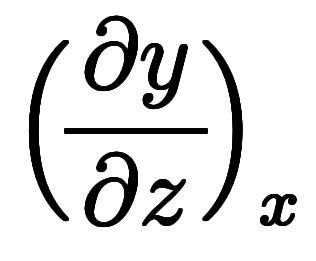
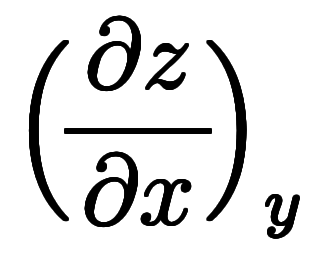

 自体は陽関数でも陰関数でも成り立つ。
自体は陽関数でも陰関数でも成り立つ。 も
も も陽微分となり、陽陽で「
も陽微分となり、陽陽で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が現れず、そのまま約分可能となる。
」が現れず、そのまま約分可能となる。 式1: |
![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が3つで「
」が3つで「![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」に、
」に、![\iro[ao]- 1 $$ \iro[ao]- 1 $$](./eq/eq-ni-915d7ad8346d8538b34b316c1493d3e2.png) なるのが容易に予想できる。
なるのが容易に予想できる。



 も
も も陰微分となり、陰陰で「
も陰微分となり、陰陰で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」は2つ現れては打ち消される。
」は2つ現れては打ち消される。 |
![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を付ければ完成:
」を付ければ完成: 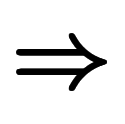     ![\iro[ak]- \ffd{b}{a} $$ \iro[ak]- \ffd{b}{a} $$](./eq/eq-ni-952126bdea71dc66bff8b6a389c94376.png) |
 と
と 自体を約分しているように見えるため、符号を気にしなくとも計算できる。
自体を約分しているように見えるため、符号を気にしなくとも計算できる。 |*微分 |*種類 |*値 | | 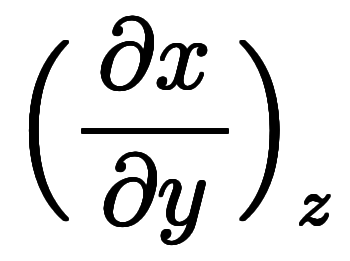 | 陰関数| | 陰関数|![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)  | | | |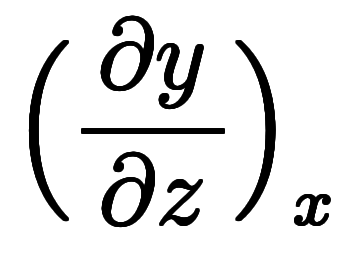 |^ | |^ |![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)  | | | |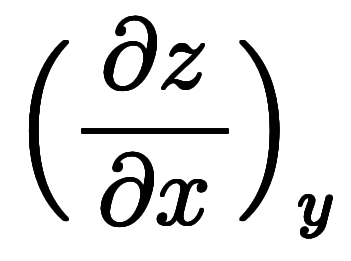 |^ | |^ |![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)  | | |
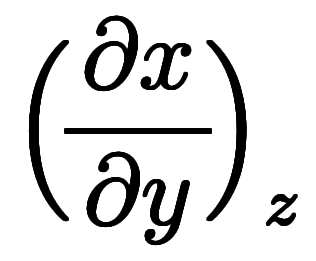 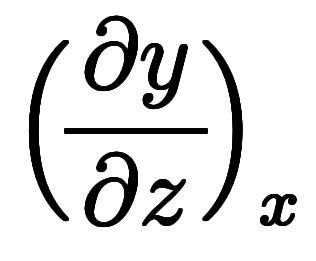 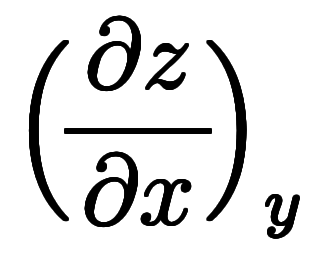  ![\Big(\! \iro[ak]- \ffd{b}{a} \!\Big) $$ \Big(\! \iro[ak]- \ffd{b}{a} \!\Big) $$](./eq/eq-ni-46cc03d3a2b7a746ced62dae384f581b.png) ![\Big(\! \iro[ak]- \ffd{c}{b} \!\Big) $$ \Big(\! \iro[ak]- \ffd{c}{b} \!\Big) $$](./eq/eq-ni-faf5bef21a2d79d89c95aeb9d39f2398.png) ![\Big(\! \iro[ak]- \ffd{a}{c} \!\Big) $$ \Big(\! \iro[ak]- \ffd{a}{c} \!\Big) $$](./eq/eq-ni-093f753525a96cb03ef3edfdd2003572.png)  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |



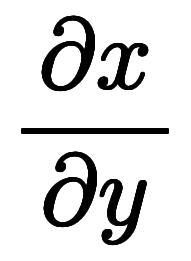

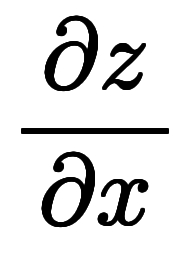

 への適応
への適応 


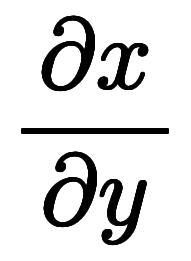

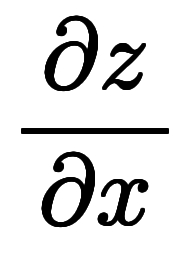

 は、 陽関数
は、 陽関数

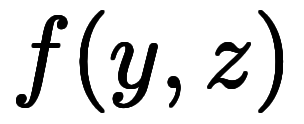 、
、

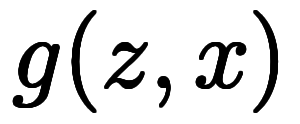 、
、

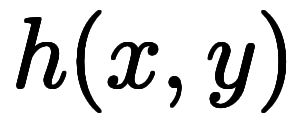 の3通りと、
の3通りと、

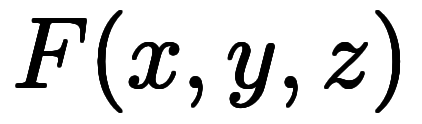 を合わせて計4通りの考え方がある。
を合わせて計4通りの考え方がある。

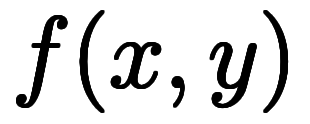 で考える場合、
で考える場合、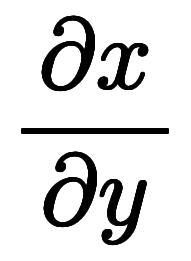 が陰微分、
が陰微分、 と
と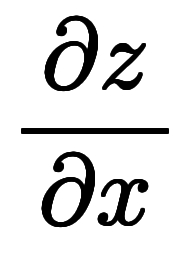 が陽微分となり、係数を約分しても陰陽陽で「
が陽微分となり、係数を約分しても陰陽陽で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が残る。
」が残る。 式2: |  | 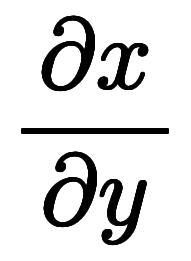  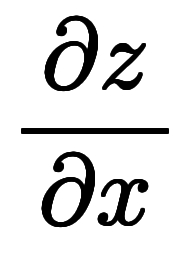  ![\Big( \iro[ak]- \ffd{a_y}{a_x} \Big) $$ \Big( \iro[ak]- \ffd{a_y}{a_x} \Big) $$](./eq/eq-ni-d47d268d4e2c41ed425768a0888374fc.png)    ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |
 を含む2つが陽微分で、残り1つが陰微分であるのが分かる。
を含む2つが陽微分で、残り1つが陰微分であるのが分かる。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が1つで「
」が1つで「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」に、
」に、![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) なるのが容易に予想できる。
なるのが容易に予想できる。



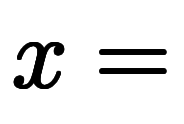
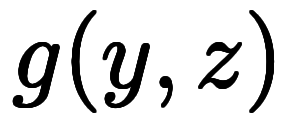 や
や

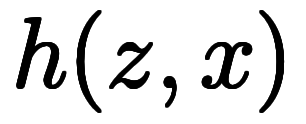 で考えても、陰になる微分が変わるだけで、1陰2陽の関係は変わらない。
で考えても、陰になる微分が変わるだけで、1陰2陽の関係は変わらない。 |
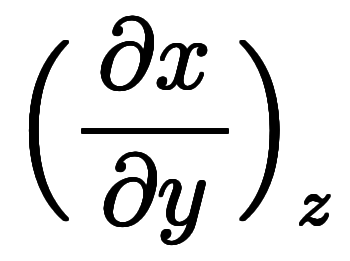 : これは陰微分のため、前節同様
: これは陰微分のため、前節同様![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)
 になる。
になる。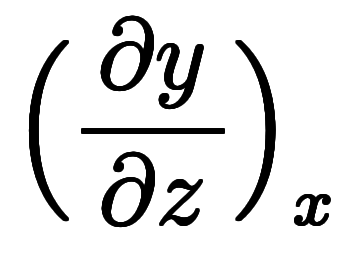 : これは陽微分だが、従属変数
: これは陽微分だが、従属変数 が下に居るため、微分係数の逆数
が下に居るため、微分係数の逆数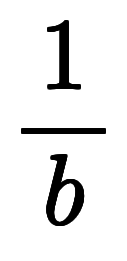 になる。
になる。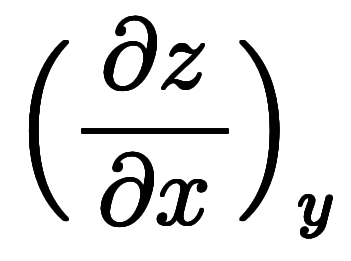 : これも陽微分で、普通に微分係数
: これも陽微分で、普通に微分係数 そのものになる。
そのものになる。

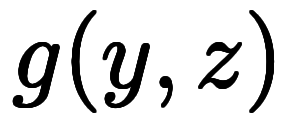

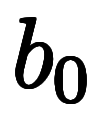

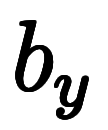


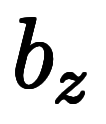

 | 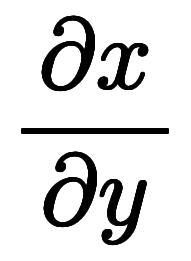  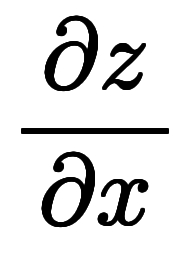  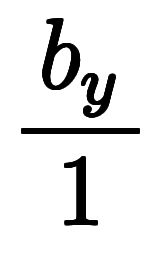 ![\Big( \iro[ak]- \ffd{b_z}{b_y} \Big) $$ \Big( \iro[ak]- \ffd{b_z}{b_y} \Big) $$](./eq/eq-ni-7da1731ecce041221ab40f9728c4da64.png) 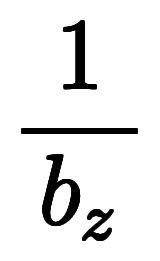  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) | |
|*微分 |*種類 |*値 | | |  | 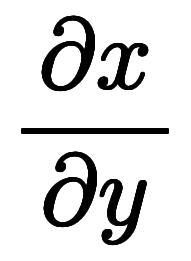  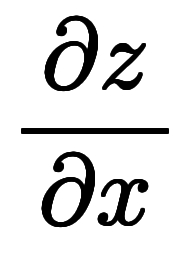  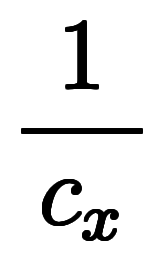 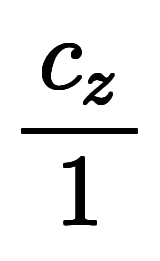 ![\Big( \iro[ak]- \ffd{c_x}{c_z} \Big) $$ \Big( \iro[ak]- \ffd{c_x}{c_z} \Big) $$](./eq/eq-ni-e22a5a846fad11ae242b5c0fddda5087.png)  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |


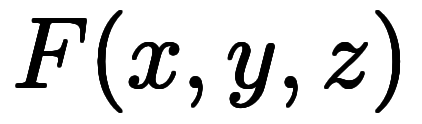 で考える場合、陰陰陰と全て陰微分になるだけで、答えは変わらない。
で考える場合、陰陰陰と全て陰微分になるだけで、答えは変わらない。 |  | 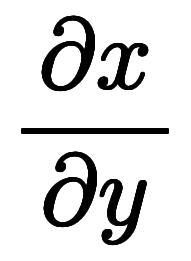  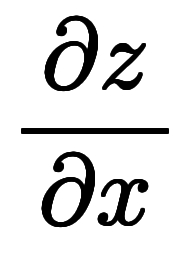  ![\Big( \iro[ak]- \ffd{k_x}{k_y} \Big) $$ \Big( \iro[ak]- \ffd{k_x}{k_y} \Big) $$](./eq/eq-ni-f2baa67454a99fb3f3102e1eec6c795e.png) ![\Big( \iro[ak]- \ffd{k_z}{k_y} \Big) $$ \Big( \iro[ak]- \ffd{k_z}{k_y} \Big) $$](./eq/eq-ni-91eef441bbd6a235e2c903382a525905.png) ![\Big( \iro[ak]- \ffd{k_x}{k_z} \Big) $$ \Big( \iro[ak]- \ffd{k_x}{k_z} \Big) $$](./eq/eq-ni-5f6f7195f1657e1be1df9877879cdede.png)  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |
 」付きの陰微分として扱うのが楽である。
」付きの陰微分として扱うのが楽である。表2:   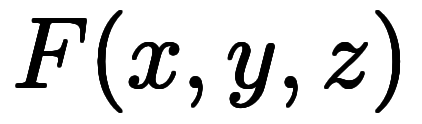 の1次近似と微分係数(参考) の1次近似と微分係数(参考) |
|---|
| 1次近似 | 微分係数 | 値 | |||
|---|---|---|---|---|---|
| 記号表記 | 関数表記 | 変数表記 |
|---|
          | ![\iro[hi]{a_y, a_z} $$ \iro[hi]{a_y, a_z} $$](./eq/eq-ni-4ac4b2eba76d35f42c904ba8c8e9bfc1.png) | ![\iro[hi]{\ppd{f}{x},\ppd{f}{y}} $$ \iro[hi]{\ppd{f}{x},\ppd{f}{y}} $$](./eq/eq-ni-1f7685714556b42704fead44268f4de6.png) | 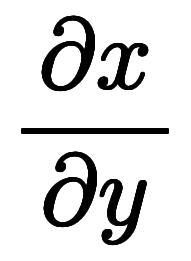   | ![\iro[ak]- \ffd{k_y}{k_x} $$ \iro[ak]- \ffd{k_y}{k_x} $$](./eq/eq-ni-7ee305a66b490c5f9f9070d8de81b971.png)  ![\iro[ak]- \ffd{k_z}{k_x} $$ \iro[ak]- \ffd{k_z}{k_x} $$](./eq/eq-ni-81d812d504717261d74e0a601a6cfa04.png) |
   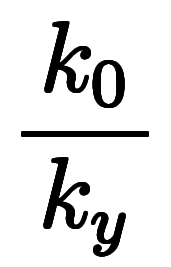       | ![\iro[hi]{b_y, b_z} $$ \iro[hi]{b_y, b_z} $$](./eq/eq-ni-5cd80dbb262d33c0e55b226c8155b3cf.png) | ![\iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$ \iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$](./eq/eq-ni-09dbcb84ed738563f857513f65e235a3.png) |   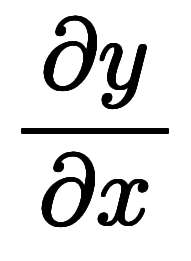 | ![\iro[ak]- \ffd{k_z}{k_y} $$ \iro[ak]- \ffd{k_z}{k_y} $$](./eq/eq-ni-351c04721b55d7e70a2677637049d2e0.png)  ![\iro[ak]- \ffd{k_x}{k_y} $$ \iro[ak]- \ffd{k_x}{k_y} $$](./eq/eq-ni-0cc029137eaad593908ef9bb1df2ac81.png) |
   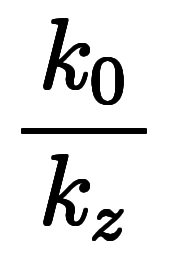       | ![\iro[hi]{c_z, c_x} $$ \iro[hi]{c_z, c_x} $$](./eq/eq-ni-259b3c99b6e44740a99e8d3867b62ffb.png) | ![\iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$ \iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$](./eq/eq-ni-37204427fdbfa2bae56fe3a9b2a33042.png) | 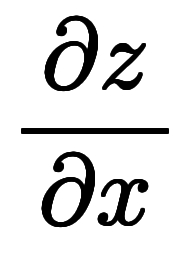   | ![\iro[ak]- \ffd{k_x}{k_z} $$ \iro[ak]- \ffd{k_x}{k_z} $$](./eq/eq-ni-8920d28711779b6e3fe8cb8d3a88957d.png)  ![\iro[ak]- \ffd{k_y}{k_z} $$ \iro[ak]- \ffd{k_y}{k_z} $$](./eq/eq-ni-c963ca958e44b758159dadf9fc937827.png) |


