![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップ(No.18) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップ(No.18) |
凌宮読取術: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
オイラーの連鎖式: |
問題は、 などを約分して
などを約分して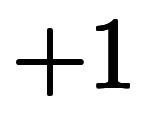 にしたどころで、そんな期待を裏切る
にしたどころで、そんな期待を裏切る![\iro[ao]-1 $$ \iro[ao]-1 $$](./eq/eq-ni-06be3155fba177d8741c844121a4ac2c.png) である。
である。
一般的な証明*2*3は式を弄り回したら合ったレベルで、とても直感的とは言えない。
しかし、それだけで「偏微分は約分できない」と諦めるのは、まだ早計である。
 が約分できる結果だけ見て、
が約分できる結果だけ見て、 を約分するから上手く行かない。
を約分するから上手く行かない。
 が約分できる原因を考えば、
が約分できる原因を考えば、 を約分は勿論、負号も問題なく処理できる。
を約分は勿論、負号も問題なく処理できる。
凌宮数学では、オイラーの連鎖式は以下のように読み替える:
|
ここで、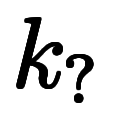 は全て係数であり、約分も符号も小学校同様に扱って良い。
は全て係数であり、約分も符号も小学校同様に扱って良い。



微分の捉え方の一つに、微分係数という考え方がある。
それは、関数の1次近似を考える際、得られる1次式の係数を微分と定義する方法である。
| 被近似関数 | 1次近似 | 微分係数 | 値 | |||
|---|---|---|---|---|---|---|
| 記号 | 関数 | 従属変数 | ||||
  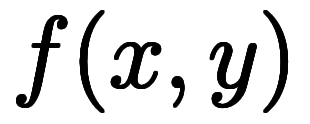 |   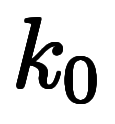  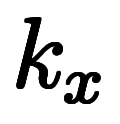     | 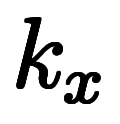   |    |    |    | |
  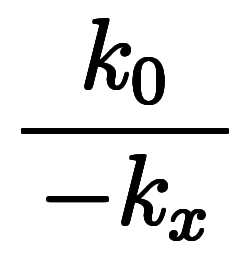     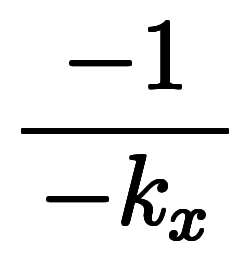  |    | ![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)    | ||||
         |   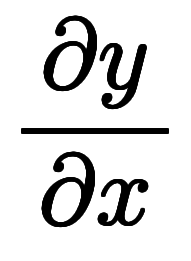 | 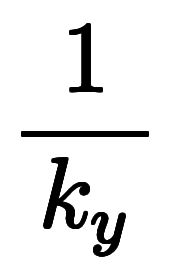  ![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)  | ||||
 や
や を計算するのに、
を計算するのに、

 の1次近似式から移項で作った式を利用した。
の1次近似式から移項で作った式を利用した。


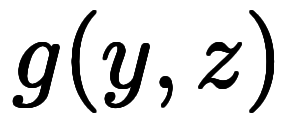 と置いて
と置いて

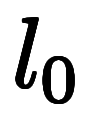

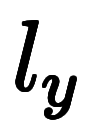


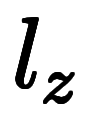
 と近似しても良いが、記号が増えるだけで計算にならない。
と近似しても良いが、記号が増えるだけで計算にならない。


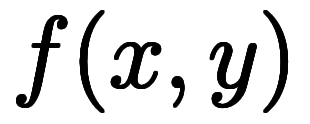 も
も

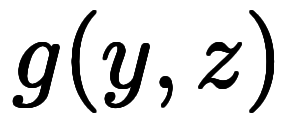 も同じ関係を記述している以上、近似式も1つ選んで使い続けば良い。
も同じ関係を記述している以上、近似式も1つ選んで使い続けば良い。
重要なのは以下の4点:
![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が生じること。
」が生じること。 にしていること。
にしていること。![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が残る。
」が残る。このため、両方とも独立変数の微分を見抜けば、「![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」を正しく扱えられる。
」を正しく扱えられる。



以上の結果を受けて、凌宮数学では以下のように陽微分と陰微分を定義する。
そうすると、関数を一次近似した式の係数の割り算で微分の値を表すとき、
陽微分には負号が付かず、陰微分には「![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が付く性質を持つ。
」が付く性質を持つ。
高校では

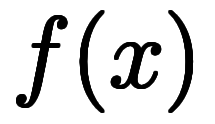 のような1変数関数しか考えないため、自ずと陽微分になる。
のような1変数関数しか考えないため、自ずと陽微分になる。
したがって、陽微分は高校からならう微分係数そのもので、いわゆる通常の微分と言える。
これに対し、陰微分は大学で黙って登場するが、係数で書くと「![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が付く新しい微分と言える。
」が付く新しい微分と言える。
陽微分で考えると、高校で習う


 は、
は、
関数を

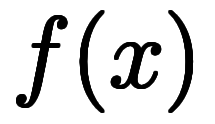 に関する2つの陽微分であり、約分できて、「
に関する2つの陽微分であり、約分できて、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が付かない、という結果になる。
」が付かない、という結果になる。
|
約分の対象は近似式の係数であるが、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が付かないため
」が付かないため と
と を消していると考えても通る。
を消していると考えても通る。
同様に、大学で習う



 は、
は、
関数を

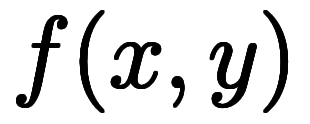 で考えると、1つの陰微分
で考えると、1つの陰微分 と2つの陽微分
と2つの陽微分 、
、 の積であるため、
の積であるため、
係数の約分は相変わらずで、符号は3つの「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」で「
」で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」になる。
」になる。
|



オイラーの連鎖式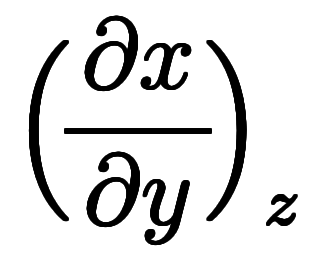
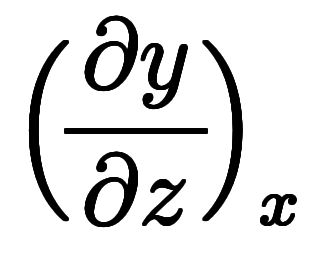
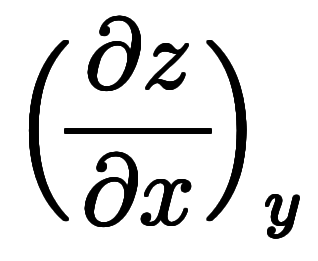

 自体は陽関数でも陰関数でも成り立つ。
自体は陽関数でも陰関数でも成り立つ。
そこで、陰関数では全ての変数を平等に扱うため、対称性の良いオイラーの連鎖式を考えるには都合が良い。
このため、まず本節で陰関数のオイラーの連鎖式を説明してから、次節で参考として陽関数のオイラーの連鎖式を説明する。
オイラーの連鎖式は3つの変数に関する公式であるため、陰関数で考える場合は3変数関数で考える必要がある:
式1: |
この時点で、オイラーの連鎖式に登場する3つの微分が全て陰微分で、掛け合わせると
・ 符号が「![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」が3つで「
」が3つで「![\iro[ao]- $$ \iro[ao]- $$](./eq/eq-ni-1be15e63f544cc448299564f146b4f26.png) 」に、
」に、
・ 大きさが分母・分子で打ち合わせて1に、
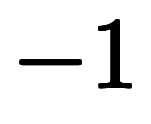
と合わせて![\iro[ao]- 1 $$ \iro[ao]- 1 $$](./eq/eq-ni-915d7ad8346d8538b34b316c1493d3e2.png) なるのが容易に予想できる。
なるのが容易に予想できる。



具体的にオイラーの連鎖式を1次近似の係数で読み替えると以下のようになる。
まず、式1を1次近似すると:
|
次に、真面目に計算しても良いが、以下のように対応する係数を逆さに書いて、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を付ければ完成:
」を付ければ完成:
|
このように作るオイラーの連鎖式に現われる3つの微分を表に纏めると:
|
したがって、陰関数のオイラーの連鎖式は以下のように読み替えできる:
|



陰関数で考えた方が例外が少なくて楽だが、
物理学や工学で扱う方程式*4の多くが陽関数になるため、参考として陽関数での読み方を説明する。
オイラーの連鎖式は3つの変数についての公式であるが、陽関数で考える場合は1つを従属変数にするため、2変数関数で済む:
式2: |
この時点で、オイラーの連鎖式に登場する3つの微分の内、 を含む2つが陽微分で、残り1つが陰微分であるのが分かる。
を含む2つが陽微分で、残り1つが陰微分であるのが分かる。
したがって、これらを掛け合わせると
・ 符号が「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が1つで「
」が1つで「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」に、
」に、
・ 大きさが分母・分子で打ち合わせて1に、
と![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) なるのが容易に予想できる。
なるのが容易に予想できる。



具体的にオイラーの連鎖式を1次近似の係数で読み替えると以下のようになる。
まず、式3を1次近似すると:
|
次は計算になるが、陽関数のため3パターンに増える:
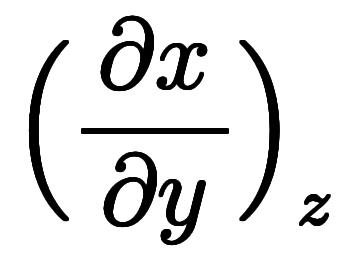 : これは陰微分のため、前節同様
: これは陰微分のため、前節同様![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png)
 になる。
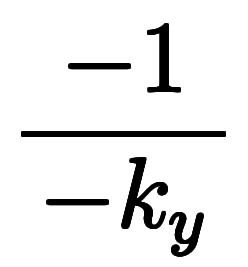
になる。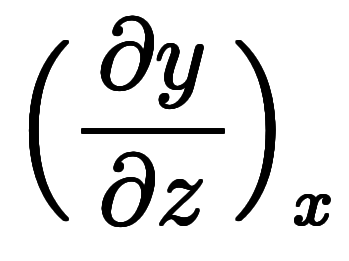 : これは陽微分だが、従属変数
: これは陽微分だが、従属変数 が下に居るため、微分係数の逆数
が下に居るため、微分係数の逆数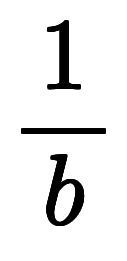 になる。
になる。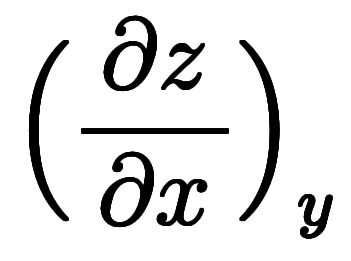 : これも陽微分で、普通に微分係数
: これも陽微分で、普通に微分係数 そのものになる。
そのものになる。以上の結果を表に纏めると:
|
したがって、陽関数のオイラーの連鎖式は以下のように読み替えできる:
|