![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップ(No.26) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップ(No.26) |
凌宮読取術: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
オイラーの連鎖式: |
問題は、 などを形式的に約分して
などを形式的に約分して と書きたいどころ、期待を裏切る
と書きたいどころ、期待を裏切る![\iro[ak]-1 $$ \iro[ak]-1 $$](./eq/eq-ni-b26c0f2a5c6ba49208b213c1e521f90d.png) である。
である。
一般的な証明*2*3は式を色々弄ったら合ったようなもので、とても直感的とは言えない。
しかし、それだけで「偏微分は約分できない」と諦めるのは、まだ勿体ない。
 が約分できる結果だけ見て、
が約分できる結果だけ見て、 をそのまま消すから上手く行かない。
をそのまま消すから上手く行かない。
 が約分できる原因を考えば、
が約分できる原因を考えば、 を約分も負号も問題なく処理できる。
を約分も負号も問題なく処理できる。
凌宮数学では、オイラーの連鎖式は以下のように読み替えて約分する:
|
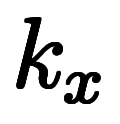 、
、 、
、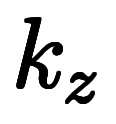 は全て普通の係数でしかないため、約分も符号処理も小学校レベルである。
は全て普通の係数でしかないため、約分も符号処理も小学校レベルである。



微分には「関数を1次近似した近似式の係数」すなわち微分係数という解釈がある。
例えば、関数

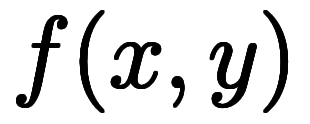 は1次式
は1次式

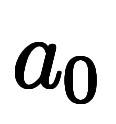

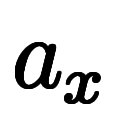


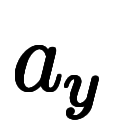
 と近似できるが、
と近似できるが、
変数 と
と の前に付く
の前に付く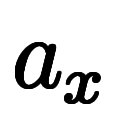 と
と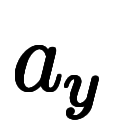 が各変数に対する微分係数で、それぞれが
が各変数に対する微分係数で、それぞれが に対する
に対する と
と の微分となる。
の微分となる。
一方で、

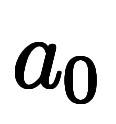

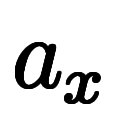


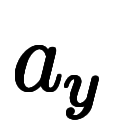
 から
から や
や につて解いた一次式からも微分係数が得られる。
につて解いた一次式からも微分係数が得られる。
例えば、 について解いた式からは、
について解いた式からは、 、
、 が得られる。
が得られる。
同様に、 について解いた式からは、
について解いた式からは、 、
、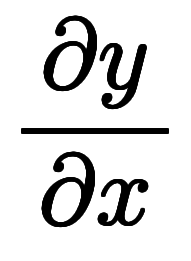 が得られる。
が得られる。
表1:   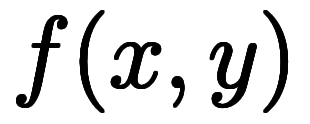 の1次近似と微分係数 の1次近似と微分係数 | ||||
|---|---|---|---|---|
| 1次近似 | 微分係数 | 値 | ||
| 係数表記 | 関数表記 | 変数表記 | ||
  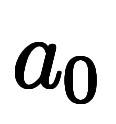  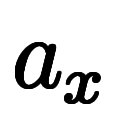   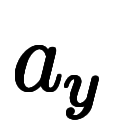  | 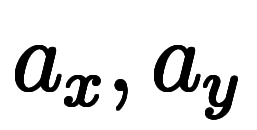 | 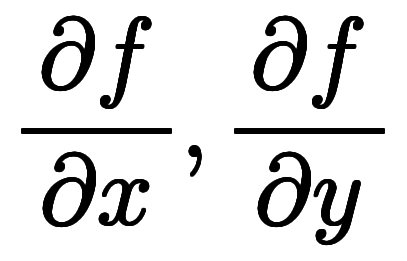 |    |    |
  ![\ffd{\iro[ak]-a_0}{a_x} $$ \ffd{\iro[ak]-a_0}{a_x} $$](./eq/eq-ni-386492f401adc6bff576e86994e118cb.png)  ![\ffd{\iro[ak]-a_y}{a_x} $$ \ffd{\iro[ak]-a_y}{a_x} $$](./eq/eq-ni-827c62a3875ee3982a8317a14d8574ff.png)     | ![\iro[hi]{b_y, b_z} $$ \iro[hi]{b_y, b_z} $$](./eq/eq-ni-5cd80dbb262d33c0e55b226c8155b3cf.png) | ![\iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$ \iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$](./eq/eq-ni-09dbcb84ed738563f857513f65e235a3.png) |    | ![\iro[ak]- \ffd{a_y}{a_x} $$ \iro[ak]- \ffd{a_y}{a_x} $$](./eq/eq-ni-de10df14b576084b352a48328f3d7dde.png)   |
  ![\ffd{\iro[ak]-a_0}{a_y} $$ \ffd{\iro[ak]-a_0}{a_y} $$](./eq/eq-ni-0306457dec638e0b90033523c1fe8826.png)     ![\ffd{\iro[ak]-a_x}{a_y} $$ \ffd{\iro[ak]-a_x}{a_y} $$](./eq/eq-ni-6b56887e798e5c3b6251fa1b4a5e9487.png)  | ![\iro[hi]{c_z, c_x} $$ \iro[hi]{c_z, c_x} $$](./eq/eq-ni-259b3c99b6e44740a99e8d3867b62ffb.png) | ![\iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$ \iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$](./eq/eq-ni-37204427fdbfa2bae56fe3a9b2a33042.png) |   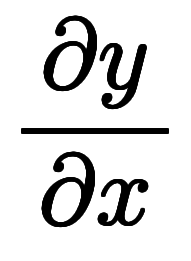 |   ![\iro[ak]- \ffd{a_x}{a_y} $$ \iro[ak]- \ffd{a_x}{a_y} $$](./eq/eq-ni-fceded1aba4e085139a06aa0134d4a3b.png) |
ここで重要なのは、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」は移項で発生するという因果関係である。
」は移項で発生するという因果関係である。
さらに、その移項は独立変数について解くためで、移項で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」つくのは別の独立変数となる。
」つくのは別の独立変数となる。
このため、分母・分子とも独立変数の微分を見抜けば、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を正しく書ける。
」を正しく書ける。
そこで、凌宮数学では以下のように陽微分と陰微分を定義する。
そうすると、関数の一次近似式の係数で微分の値を表すとき、微分の陰陽で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」の有無を判定できる。
」の有無を判定できる。
![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」有り
」有り![\iro[kr]- $$ \iro[kr]- $$](./eq/eq-ni-9b705174bef0f0403f453c5e8265c584.png) 」無し
」無し


 への適応
への適応 


高校で習う


 は、陽関数を
は、陽関数を

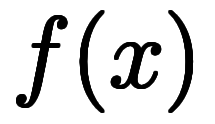 と陰関数
と陰関数

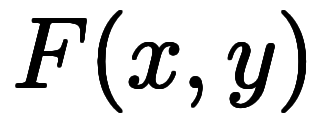 の2通りの考え方がある。
の2通りの考え方がある。
陽関数で考える場合、 も
も も陽微分となり、「
も陽微分となり、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が現れず、そのまま約分可能となる。
」が現れず、そのまま約分可能となる。
|
陰関数で考える場合、 も
も も陰微分となり、「
も陰微分となり、「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」は2つ現れるが、打ち消し合って消える。
」は2つ現れるが、打ち消し合って消える。
|
どちらの結果も と
と 自体を約分しているように見えるため、符号を気にしなくても計算はできた。
自体を約分しているように見えるため、符号を気にしなくても計算はできた。




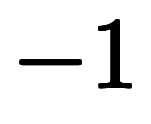 への適応
への適応 


大学で習う



 は、陽関数
は、陽関数

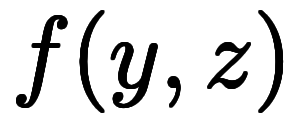 、
、

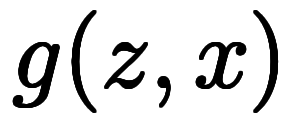 、
、

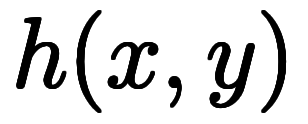 の3通りと、陰関数
の3通りと、陰関数

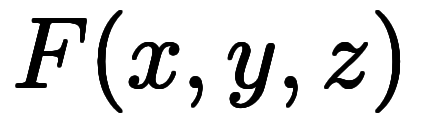 を合わせて計4通りで考えられる。
を合わせて計4通りで考えられる。
陽関数

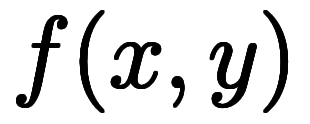 で考える場合、
で考える場合、
 が陰微分、
が陰微分、 と
と が陽微分となり、係数を約分しても「
が陽微分となり、係数を約分しても「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が残る。
」が残る。
|
|
|
陽関数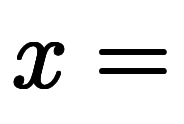
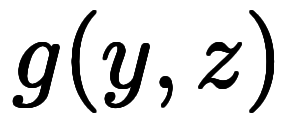 や
や

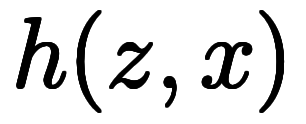 で考えても、陰になる微分が変わるだけで、1陰2陽の関係は変わらない。
で考えても、陰になる微分が変わるだけで、1陰2陽の関係は変わらない。
|
|
|
|
|
|



これまで、



 に対し、
に対し、


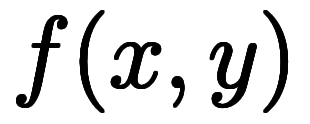 や
や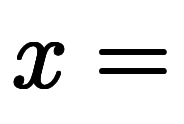
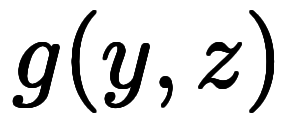 、
、

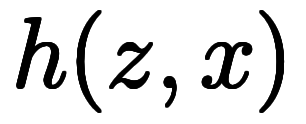 と好きな関数を置いて陰微分と陽微分を考えてきた。
と好きな関数を置いて陰微分と陽微分を考えてきた。


 自体は関数に依らないため、結果が関数に依らないのは当然である。
自体は関数に依らないため、結果が関数に依らないのは当然である。
3つの変数 、
、 、
、 の関係を記述する関数に、次の陰関数というのもある*5。
の関係を記述する関数に、次の陰関数というのもある*5。


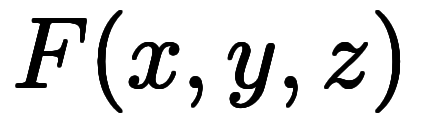
もっとも、

 には従属変数と独立変数の区別も無く、対称的である。
には従属変数と独立変数の区別も無く、対称的である。
このため、従属変数と独立変数を区別せず皆平等に扱う陰関数で考えた方が簡潔だったりする:
|
|
|
形式上、陰関数では全ての変数が独立変数と見なせるため、陰関数の微分は全て陰微分になる。
表2:   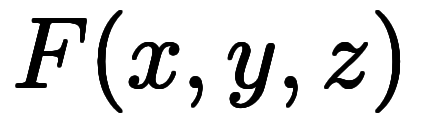 の1次近似と微分係数(参考) の1次近似と微分係数(参考) | |||||
|---|---|---|---|---|---|
| 1次近似 | 微分係数 | 値 | |||
| 記号表記 | 関数表記 | 変数表記 | |||
  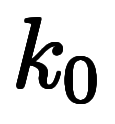  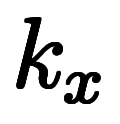      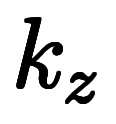  | 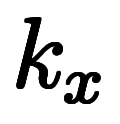    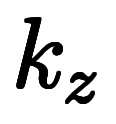 |     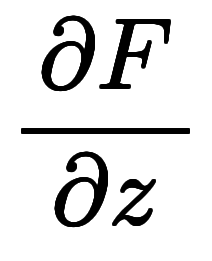 | *6 | 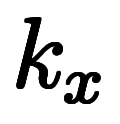    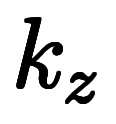 | |
          | ![\iro[hi]{a_y, a_z} $$ \iro[hi]{a_y, a_z} $$](./eq/eq-ni-4ac4b2eba76d35f42c904ba8c8e9bfc1.png) | ![\iro[hi]{\ppd{f}{x},\ppd{f}{y}} $$ \iro[hi]{\ppd{f}{x},\ppd{f}{y}} $$](./eq/eq-ni-1f7685714556b42704fead44268f4de6.png) |    | ![\iro[ak]- \ffd{k_y}{k_x} $$ \iro[ak]- \ffd{k_y}{k_x} $$](./eq/eq-ni-7ee305a66b490c5f9f9070d8de81b971.png)  ![\iro[ak]- \ffd{k_z}{k_x} $$ \iro[ak]- \ffd{k_z}{k_x} $$](./eq/eq-ni-81d812d504717261d74e0a601a6cfa04.png) | |
   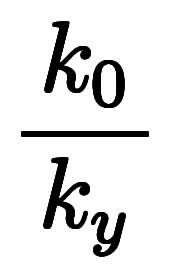       | ![\iro[hi]{b_y, b_z} $$ \iro[hi]{b_y, b_z} $$](./eq/eq-ni-5cd80dbb262d33c0e55b226c8155b3cf.png) | ![\iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$ \iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$](./eq/eq-ni-09dbcb84ed738563f857513f65e235a3.png) |   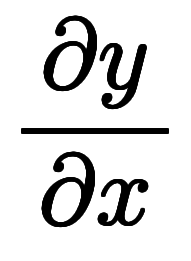 | ![\iro[ak]- \ffd{k_z}{k_y} $$ \iro[ak]- \ffd{k_z}{k_y} $$](./eq/eq-ni-351c04721b55d7e70a2677637049d2e0.png)  ![\iro[ak]- \ffd{k_x}{k_y} $$ \iro[ak]- \ffd{k_x}{k_y} $$](./eq/eq-ni-0cc029137eaad593908ef9bb1df2ac81.png) | |
   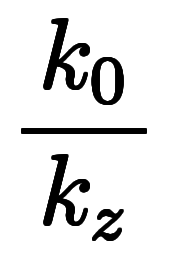       | ![\iro[hi]{c_z, c_x} $$ \iro[hi]{c_z, c_x} $$](./eq/eq-ni-259b3c99b6e44740a99e8d3867b62ffb.png) | ![\iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$ \iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$](./eq/eq-ni-37204427fdbfa2bae56fe3a9b2a33042.png) |    | ![\iro[ak]- \ffd{k_x}{k_z} $$ \iro[ak]- \ffd{k_x}{k_z} $$](./eq/eq-ni-8920d28711779b6e3fe8cb8d3a88957d.png)  ![\iro[ak]- \ffd{k_y}{k_z} $$ \iro[ak]- \ffd{k_y}{k_z} $$](./eq/eq-ni-c963ca958e44b758159dadf9fc937827.png) | |



以上より、オイラーの連鎖式で登場する微分は、高校で習うと性質が異なる。
それも常微分と偏微分の違いではなく、被微分変数と微分変数の関係が原因である。
微分の基本である微分係数に立ち戻れば、ちゃんと小学校レベルの約分になる。
「微分は分数ではないので約分できない」ではなく、「偏微分だから約分できない」でもなく、
「微分から近似式の係数には簡単に変換でき、係数であれば約分できる」と教えて欲しい。