![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップの現在との差分(No.4) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップの現在との差分(No.4) |
猫式読取術:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
オイラーの連鎖式:     ![\iro[ak]-1 $$ \iro[ak]-1 $$](./eq/eq-ni-b26c0f2a5c6ba49208b213c1e521f90d.png) |
 などを形式的に約分して
などを形式的に約分して と書きたいどころ、期待を裏切る
と書きたいどころ、期待を裏切る![\iro[ak]-1 $$ \iro[ak]-1 $$](./eq/eq-ni-b26c0f2a5c6ba49208b213c1e521f90d.png) である。
である。 が約分できる結果だけ見て
が約分できる結果だけ見て をそのまま消すから、計算が上手く行かない。
をそのまま消すから、計算が上手く行かない。 が約分できる仕組みを見て
が約分できる仕組みを見て を正しく読み替えると、約分も負号も直観的に考えられる。
を正しく読み替えると、約分も負号も直観的に考えられる。 オイラーの連鎖式: |
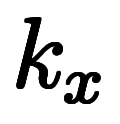 、
、 、
、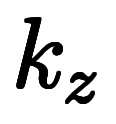 は全て普通の係数でしかないため、約分も符号処理も小学校レベルで済む。問題は、もし右辺が
は全て普通の係数でしかないため、約分も符号処理も小学校レベルで済む。問題は、もし右辺が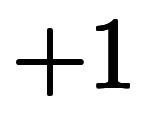 ならば、恐らく誰もが「分子の
ならば、恐らく誰もが「分子の と分母の
と分母の が打ち消して…」と簡単に納得できるところ、残念ながら
が打ち消して…」と簡単に納得できるところ、残念ながら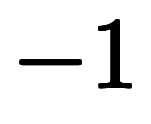 である。特に覚えにくいワケではないが、導出には結構手間が掛かる*5*6。というわけで、直感的イメージできる方が式変形が楽である。
である。特に覚えにくいワケではないが、導出には結構手間が掛かる*5*6。というわけで、直感的イメージできる方が式変形が楽である。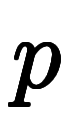 、体積
、体積 、温度
、温度 を結ぶマクスウェルの規則
を結ぶマクスウェルの規則
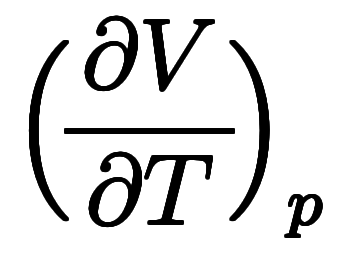
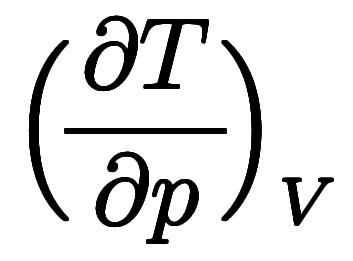

 の形で学ぶことになる。
の形で学ぶことになる。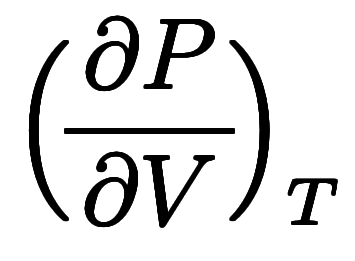
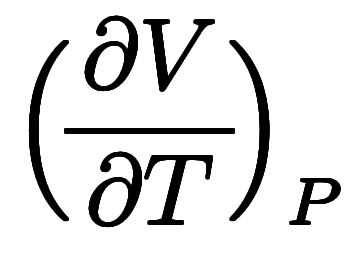
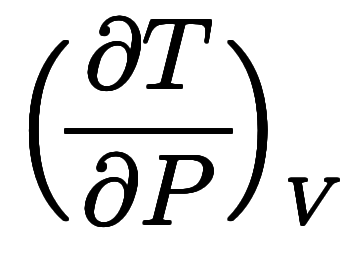

 の形で学ぶことになる。
の形で学ぶことになる。





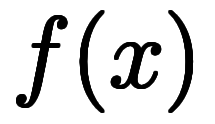 について、各点
について、各点 において直線
において直線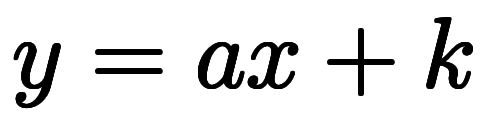 で近似しようとするとき、係数
で近似しようとするとき、係数

 となる。これが微分値が微分係数と呼ばれる故でもある。同様に、任意の2変数関数
となる。これが微分値が微分係数と呼ばれる故でもある。同様に、任意の2変数関数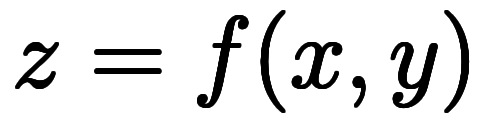 について、直線の代わりに平面
について、直線の代わりに平面 で近似できる。この場合、
で近似できる。この場合、

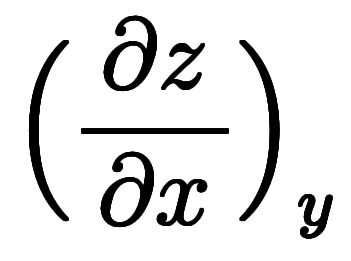 、
、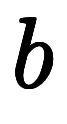

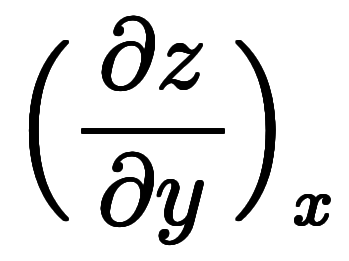 となる。ここで、近似平面は
となる。ここで、近似平面は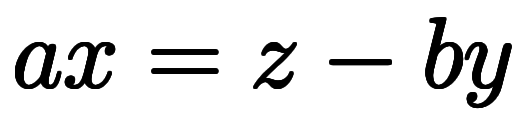 に変形できるため、
に変形できるため、![\ppd{x}{y} = \iro[ak]{-} \ffd{b}{a} $$ \ppd{x}{y} = \iro[ak]{-} \ffd{b}{a} $$](./eq/eq-ni-b3cecd119945346ffb89cb505b2dbea9.png) が得られる。
が得られる。 と
と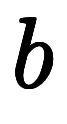 を代入すると、
を代入すると、![\Big( \ppd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{z}{y} \Big)_x}{\Big( \ppd{z}{x} \Big)_y} $$ \Big( \ppd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{z}{y} \Big)_x}{\Big( \ppd{z}{x} \Big)_y} $$](./eq/eq-ni-4df4bc79356d79436861399e56bb5cad.png) になる。したがって、
になる。したがって、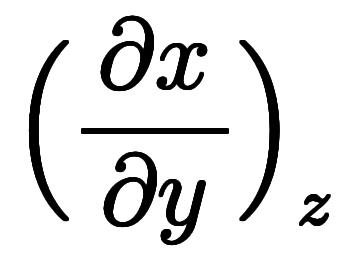 に
に

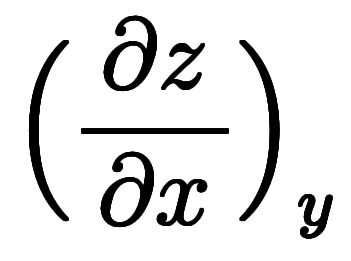 と
と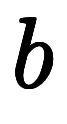

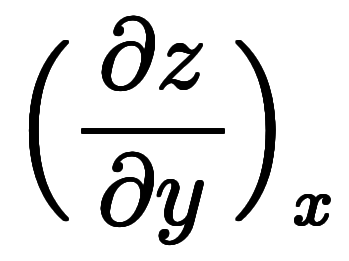 を掛け合わせると、大きさが打ち消して
を掛け合わせると、大きさが打ち消して となり、
となり、![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) が残る。
が残る。





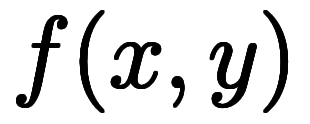 は1次式
は1次式

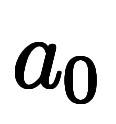

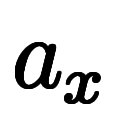


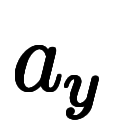
 と近似できるが、
と近似できるが、 と
と の係数
の係数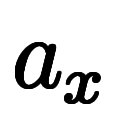 と
と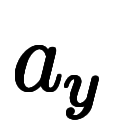 が微分係数で、それぞれが
が微分係数で、それぞれが の偏微分
の偏微分 、
、 となる。
となる。

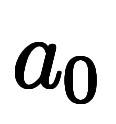

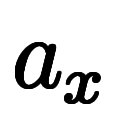


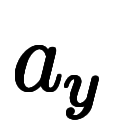
 から
から や
や につて解いた一次式からも微分係数が得られる。
につて解いた一次式からも微分係数が得られる。 について解いた式からは、
について解いた式からは、 、
、 が得られる。
が得られる。 について解いた式からは、
について解いた式からは、 、
、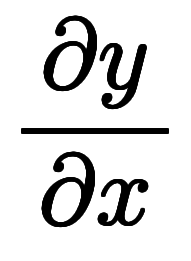 が得られる。
が得られる。表1:   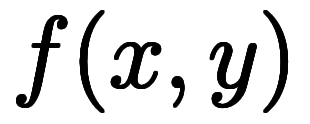 の1次近似と微分係数 の1次近似と微分係数 |
|---|
| 1次近似 | 微分係数 | 値 | ||
|---|---|---|---|---|
| 係数表記 | 関数表記 | 変数表記 |
|---|
  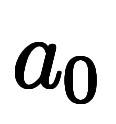  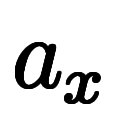   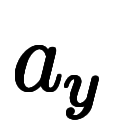  | 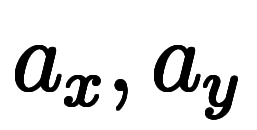 | 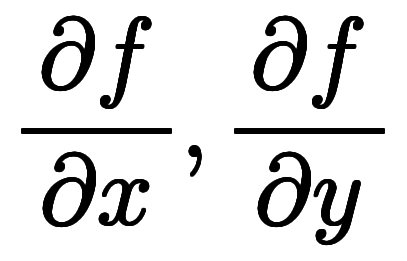 |    |    |
  ![\ffd{\iro[ak]-a_0}{a_x} $$ \ffd{\iro[ak]-a_0}{a_x} $$](./eq/eq-ni-386492f401adc6bff576e86994e118cb.png)  ![\ffd{\iro[ak]-a_y}{a_x} $$ \ffd{\iro[ak]-a_y}{a_x} $$](./eq/eq-ni-827c62a3875ee3982a8317a14d8574ff.png)     | ![\iro[hi]{b_y, b_z} $$ \iro[hi]{b_y, b_z} $$](./eq/eq-ni-5cd80dbb262d33c0e55b226c8155b3cf.png) | ![\iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$ \iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$](./eq/eq-ni-09dbcb84ed738563f857513f65e235a3.png) |    | ![\iro[ak]- \ffd{a_y}{a_x} $$ \iro[ak]- \ffd{a_y}{a_x} $$](./eq/eq-ni-de10df14b576084b352a48328f3d7dde.png)   |
  ![\ffd{\iro[ak]-a_0}{a_y} $$ \ffd{\iro[ak]-a_0}{a_y} $$](./eq/eq-ni-0306457dec638e0b90033523c1fe8826.png)     ![\ffd{\iro[ak]-a_x}{a_y} $$ \ffd{\iro[ak]-a_x}{a_y} $$](./eq/eq-ni-6b56887e798e5c3b6251fa1b4a5e9487.png)  | ![\iro[hi]{c_z, c_x} $$ \iro[hi]{c_z, c_x} $$](./eq/eq-ni-259b3c99b6e44740a99e8d3867b62ffb.png) | ![\iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$ \iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$](./eq/eq-ni-37204427fdbfa2bae56fe3a9b2a33042.png) |   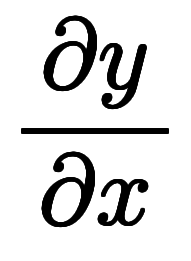 |   ![\iro[ak]- \ffd{a_x}{a_y} $$ \iro[ak]- \ffd{a_x}{a_y} $$](./eq/eq-ni-fceded1aba4e085139a06aa0134d4a3b.png) |
![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が発生することである。
」が発生することである。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」付くのは別の独立変数の項に限る。
」付くのは別の独立変数の項に限る。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」を正しく書ける。
」を正しく書ける。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」の有無を判定できる。
」の有無を判定できる。![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」有り
」有り![\iro[kr]- $$ \iro[kr]- $$](./eq/eq-ni-9b705174bef0f0403f453c5e8265c584.png) 」無し
」無し




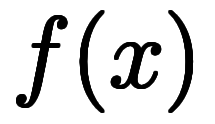 について、
について、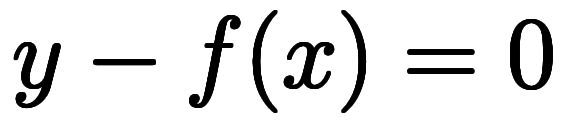 と変形でき、左辺を纏めて
と変形でき、左辺を纏めて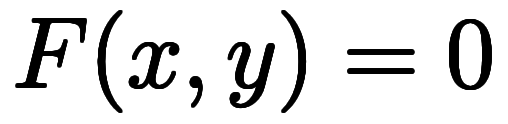 とおける。この関係では、
とおける。この関係では、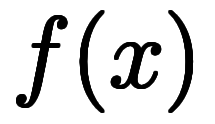 を陽関数、
を陽関数、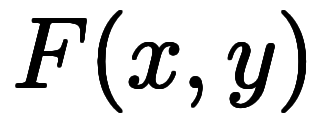 を陰関数と呼ばれる。式の見た目では、陽関数は1つの変数を特別扱いするのに対し、陰関数では全ての変数について対称的な表記になっている。陰関数で考える場合、1変数関数
を陰関数と呼ばれる。式の見た目では、陽関数は1つの変数を特別扱いするのに対し、陰関数では全ての変数について対称的な表記になっている。陰関数で考える場合、1変数関数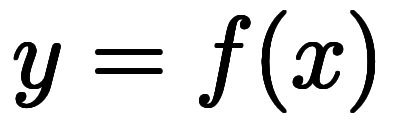 に対する陰関数
に対する陰関数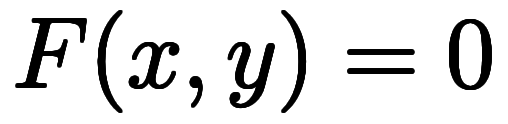 は
は で近似することになる。その結果、
で近似することになる。その結果、

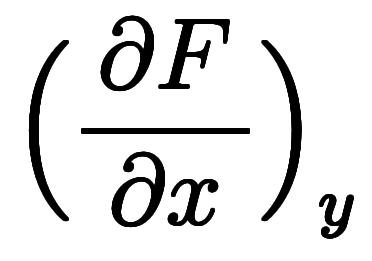 、
、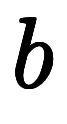

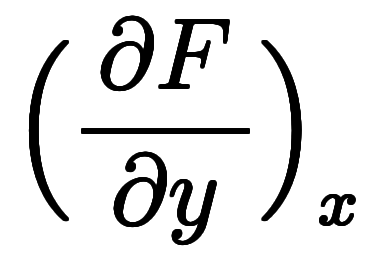 となり、
となり、![\ddd{x}{y} = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_y}{\Big( \ppd{F}{y} \Big)_x} $$ \ddd{x}{y} = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_y}{\Big( \ppd{F}{y} \Big)_x} $$](./eq/eq-ni-73149caaaab3136de54ba520edc1acc7.png) になる。同様に、2変数関数
になる。同様に、2変数関数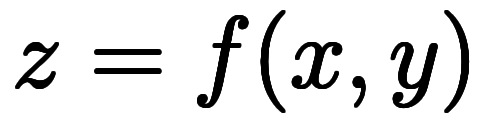 に対する陰関数
に対する陰関数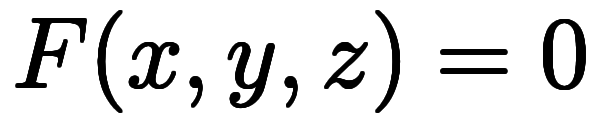 の場合は
の場合は で近似することになる。
で近似することになる。その結果、


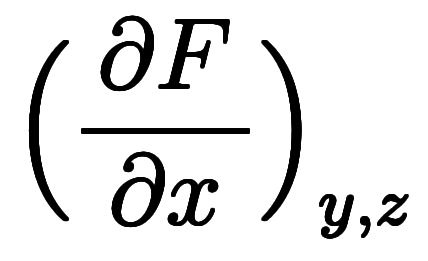 、
、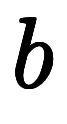

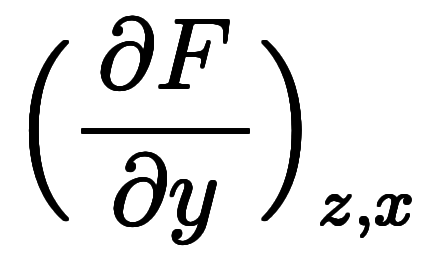 、
、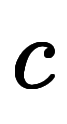

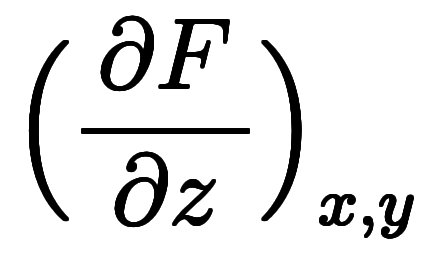 となり、
となり、![\Big( \ddd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_{y,z}}{\Big( \ppd{F}{y} \Big)_{z,x}} $$ \Big( \ddd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_{y,z}}{\Big( \ppd{F}{y} \Big)_{z,x}} $$](./eq/eq-ni-a48e6ba23d0b37af240faad740f4b120.png) 、
、
![\Big( \ddd{y}{z} \Big)_x = \iro[ak]{-} \ffd{\Big( \ppd{F}{y} \Big)_{z,x}}{\Big( \ppd{F}{z} \Big)_{x,y}} $$ \Big( \ddd{y}{z} \Big)_x = \iro[ak]{-} \ffd{\Big( \ppd{F}{y} \Big)_{z,x}}{\Big( \ppd{F}{z} \Big)_{x,y}} $$](./eq/eq-ni-14c260a3d086fedc69053cff5bcc028c.png) 、
、![\Big( \ddd{z}{x} \Big)_y = \iro[ak]{-} \ffd{\Big( \ppd{F}{z} \Big)_{x,y}}{\Big( \ppd{F}{x} \Big)_{y,z}} $$ \Big( \ddd{z}{x} \Big)_y = \iro[ak]{-} \ffd{\Big( \ppd{F}{z} \Big)_{x,y}}{\Big( \ppd{F}{x} \Big)_{y,z}} $$](./eq/eq-ni-058c51a929256e9ac002b875cda2a8ee.png) になる。したがって、3つの偏微分を掛け合わせると、大きさが打ち消して
になる。したがって、3つの偏微分を掛け合わせると、大きさが打ち消して となり、
となり、![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) が残る。
が残る。



 への適応
への適応 





 は、陽関数
は、陽関数

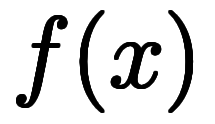 と陰関数
と陰関数

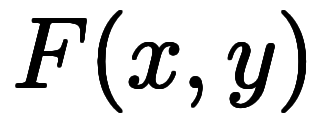 の2通りの考え方がある。
の2通りの考え方がある。 も
も も陽微分となり、陽陽で「
も陽微分となり、陽陽で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が現れず、そのまま約分可能となる。
」が現れず、そのまま約分可能となる。  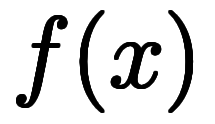  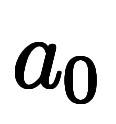  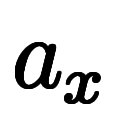  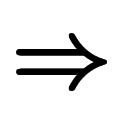        |
 も
も も陰微分となり、陰陰で「
も陰微分となり、陰陰で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」は2つ現れては打ち消される。
」は2つ現れては打ち消される。  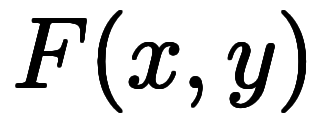  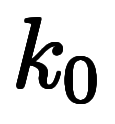  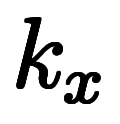   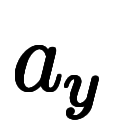      ![\Big( \iro[ak]- \ffd{a_x}{a_y} \Big) $$ \Big( \iro[ak]- \ffd{a_x}{a_y} \Big) $$](./eq/eq-ni-bcaaacd2e7cd7e2d630c108f8290b6e9.png) ![\Big( \iro[ak]- \ffd{a_y}{a_x} \Big) $$ \Big( \iro[ak]- \ffd{a_y}{a_x} \Big) $$](./eq/eq-ni-d47d268d4e2c41ed425768a0888374fc.png)   |
 と
と 自体を約分しているように見えるため、符号を気にしなくとも計算できる。
自体を約分しているように見えるため、符号を気にしなくとも計算できる。



![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) 」の現れるタイミングである。陽関数の
」の現れるタイミングである。陽関数の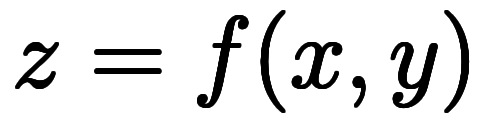 も、陰関数の
も、陰関数の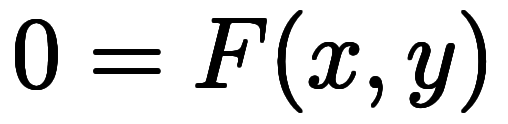 も、ある意味では同じ形をしている。ここでの陰陽とは関数値を変数として扱うかどうかの違いである。そこで、
も、ある意味では同じ形をしている。ここでの陰陽とは関数値を変数として扱うかどうかの違いである。そこで、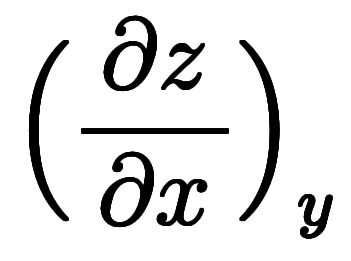

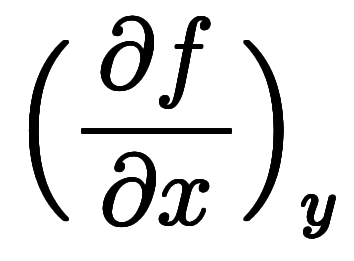 や
や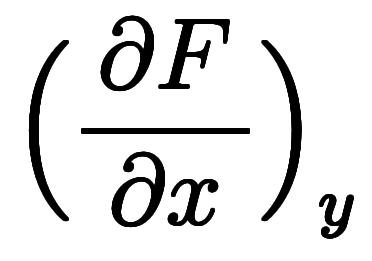 のように関数値を含む微分を「陽的な傾き」と、
のように関数値を含む微分を「陽的な傾き」と、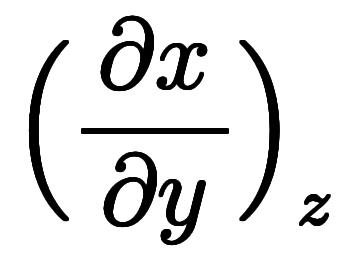 や
や のように独立変数間の微分を「陰的な傾き」と、直感的に捕らえられる。そうすると、まず、陽的傾きは形式的にプラスの式になる。これが一般的な傾きの感覚に一致する。次に、陰的な傾きは形式的にマイナスの式になる。この感覚があれば、オイラーの連鎖式は直感的に理解できるようになる。纏めて、
のように独立変数間の微分を「陰的な傾き」と、直感的に捕らえられる。そうすると、まず、陽的傾きは形式的にプラスの式になる。これが一般的な傾きの感覚に一致する。次に、陰的な傾きは形式的にマイナスの式になる。この感覚があれば、オイラーの連鎖式は直感的に理解できるようになる。纏めて、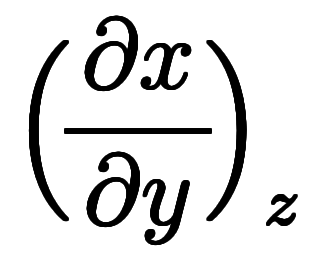
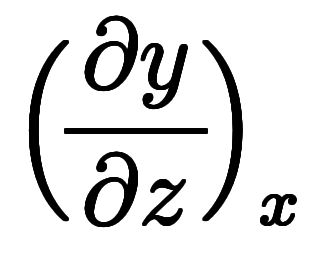
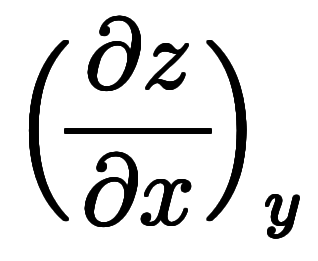 の意味は、
の意味は、



 は、 陽関数
は、 陽関数

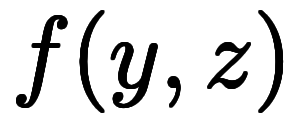 、
、

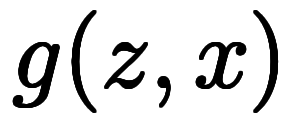 、
、

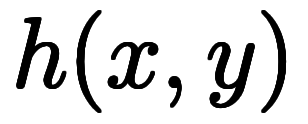 の3通りと、
の3通りと、

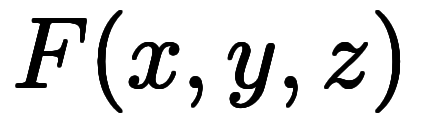 を合わせて計4通りの考え方がある。陽関数
を合わせて計4通りの考え方がある。陽関数

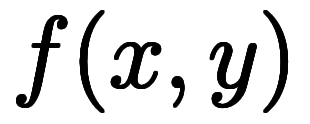 で考える場合、
で考える場合、 が陰微分、
が陰微分、 と
と が陽微分となり、係数を約分しても陰陽陽で「
が陽微分となり、係数を約分しても陰陽陽で「![\iro[ak]- $$ \iro[ak]- $$](./eq/eq-ni-ca39963766973534592b7618bfd002ec.png) 」が残る。
」が残る。  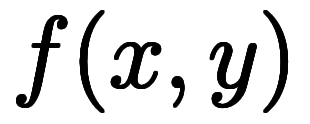  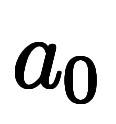  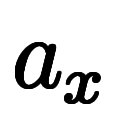   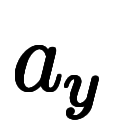  |  |     ![\Big( \iro[ak]- \ffd{a_y}{a_x} \Big) $$ \Big( \iro[ak]- \ffd{a_y}{a_x} \Big) $$](./eq/eq-ni-d47d268d4e2c41ed425768a0888374fc.png)    ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |
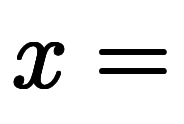
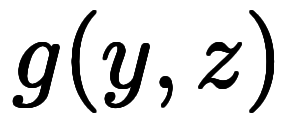 や
や

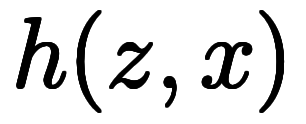 で考えても、陰になる微分が変わるだけで、1陰2陽の関係は変わらない。
で考えても、陰になる微分が変わるだけで、1陰2陽の関係は変わらない。  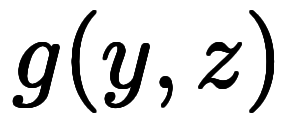  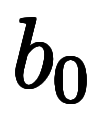  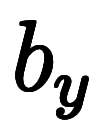   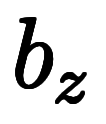  |  |     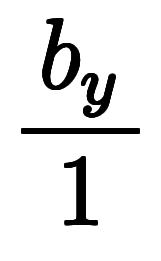 ![\Big( \iro[ak]- \ffd{b_z}{b_y} \Big) $$ \Big( \iro[ak]- \ffd{b_z}{b_y} \Big) $$](./eq/eq-ni-7da1731ecce041221ab40f9728c4da64.png) 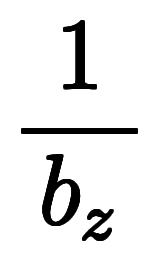  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |
  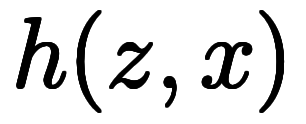    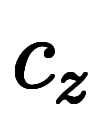   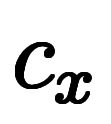  |  |     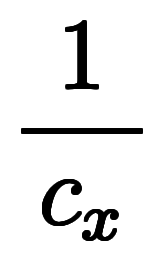 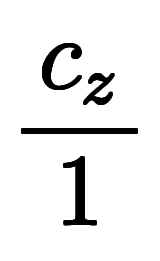 ![\Big( \iro[ak]- \ffd{c_x}{c_z} \Big) $$ \Big( \iro[ak]- \ffd{c_x}{c_z} \Big) $$](./eq/eq-ni-e22a5a846fad11ae242b5c0fddda5087.png)  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |


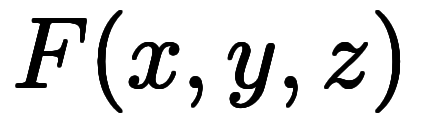 で考える場合、陰陰陰と全て陰微分になるだけで、答えは変わらない。
で考える場合、陰陰陰と全て陰微分になるだけで、答えは変わらない。  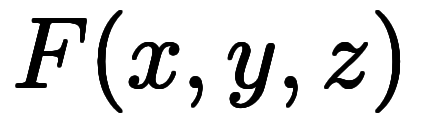  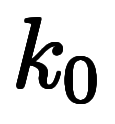  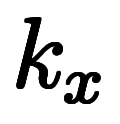      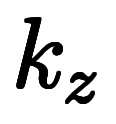  |  |     ![\Big( \iro[ak]- \ffd{k_x}{k_y} \Big) $$ \Big( \iro[ak]- \ffd{k_x}{k_y} \Big) $$](./eq/eq-ni-f2baa67454a99fb3f3102e1eec6c795e.png) ![\Big( \iro[ak]- \ffd{k_z}{k_y} \Big) $$ \Big( \iro[ak]- \ffd{k_z}{k_y} \Big) $$](./eq/eq-ni-91eef441bbd6a235e2c903382a525905.png) ![\Big( \iro[ak]- \ffd{k_x}{k_z} \Big) $$ \Big( \iro[ak]- \ffd{k_x}{k_z} \Big) $$](./eq/eq-ni-5f6f7195f1657e1be1df9877879cdede.png)  ![\iro[ak]- 1 $$ \iro[ak]- 1 $$](./eq/eq-ni-93791d74a959496c3d49fbeafe1c4a2e.png) |
 」付きの陰微分として扱うのが楽である。
」付きの陰微分として扱うのが楽である。表2:   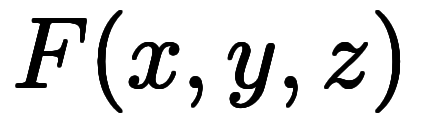 の1次近似と微分係数(参考) の1次近似と微分係数(参考) |
|---|
| 1次近似 | 微分係数 | 値 | |||
|---|---|---|---|---|---|
| 記号表記 | 関数表記 | 変数表記 |
|---|
          | ![\iro[hi]{a_y, a_z} $$ \iro[hi]{a_y, a_z} $$](./eq/eq-ni-4ac4b2eba76d35f42c904ba8c8e9bfc1.png) | ![\iro[hi]{\ppd{f}{x},\ppd{f}{y}} $$ \iro[hi]{\ppd{f}{x},\ppd{f}{y}} $$](./eq/eq-ni-1f7685714556b42704fead44268f4de6.png) |    | ![\iro[ak]- \ffd{k_y}{k_x} $$ \iro[ak]- \ffd{k_y}{k_x} $$](./eq/eq-ni-7ee305a66b490c5f9f9070d8de81b971.png)  ![\iro[ak]- \ffd{k_z}{k_x} $$ \iro[ak]- \ffd{k_z}{k_x} $$](./eq/eq-ni-81d812d504717261d74e0a601a6cfa04.png) |
   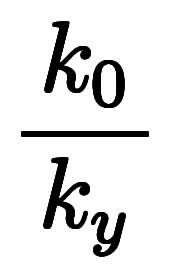       | ![\iro[hi]{b_y, b_z} $$ \iro[hi]{b_y, b_z} $$](./eq/eq-ni-5cd80dbb262d33c0e55b226c8155b3cf.png) | ![\iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$ \iro[hi]{\ppd{g}{y},\ppd{g}{z}} $$](./eq/eq-ni-09dbcb84ed738563f857513f65e235a3.png) |   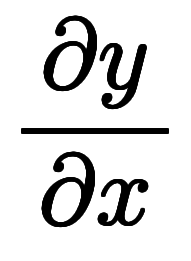 | ![\iro[ak]- \ffd{k_z}{k_y} $$ \iro[ak]- \ffd{k_z}{k_y} $$](./eq/eq-ni-351c04721b55d7e70a2677637049d2e0.png)  ![\iro[ak]- \ffd{k_x}{k_y} $$ \iro[ak]- \ffd{k_x}{k_y} $$](./eq/eq-ni-0cc029137eaad593908ef9bb1df2ac81.png) |
   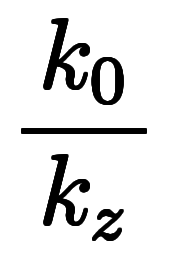       | ![\iro[hi]{c_z, c_x} $$ \iro[hi]{c_z, c_x} $$](./eq/eq-ni-259b3c99b6e44740a99e8d3867b62ffb.png) | ![\iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$ \iro[hi]{\ppd{h}{z},\ppd{h}{x}} $$](./eq/eq-ni-37204427fdbfa2bae56fe3a9b2a33042.png) |    | ![\iro[ak]- \ffd{k_x}{k_z} $$ \iro[ak]- \ffd{k_x}{k_z} $$](./eq/eq-ni-8920d28711779b6e3fe8cb8d3a88957d.png)  ![\iro[ak]- \ffd{k_y}{k_z} $$ \iro[ak]- \ffd{k_y}{k_z} $$](./eq/eq-ni-c963ca958e44b758159dadf9fc937827.png) |


