![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップ(No.8) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
オイラーの連鎖式 のバックアップ(No.8) |
猫式読取術: |
オイラーの連鎖式: |
問題は、もし右辺が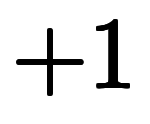 ならば、恐らく誰もが「分子の
ならば、恐らく誰もが「分子の と分母の
と分母の が打ち消して…」と簡単に納得できるところ、残念ながら
が打ち消して…」と簡単に納得できるところ、残念ながら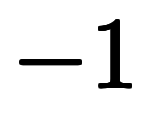 である。
である。
特に覚えにくいワケではないが、導出には結構手間が掛かる*2*3。というわけで、直感的イメージできる方が式変形が楽である。
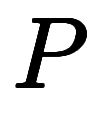 、体積
、体積 、温度
、温度 を結ぶマクスウェルの規則
を結ぶマクスウェルの規則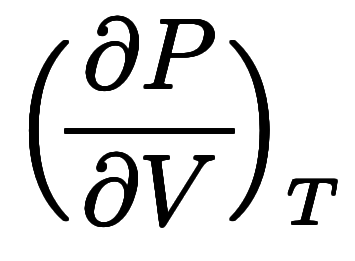
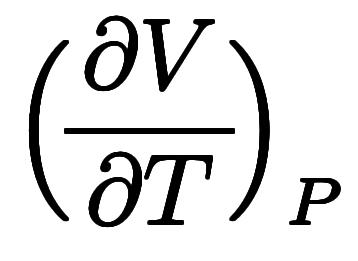
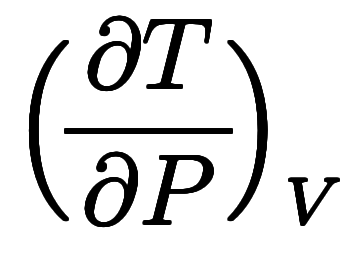

 の形で学ぶことになる。
の形で学ぶことになる。


任意の1変数関数

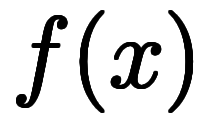 について、各点
について、各点 において直線
において直線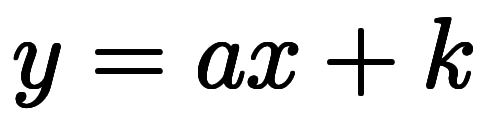 で近似しようとするとき、係数
で近似しようとするとき、係数

 となる。この微分係数というのが微分の根源である。
となる。この微分係数というのが微分の根源である。
同様に、任意の2変数関数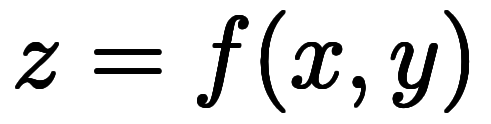 について、直線の代わりに平面
について、直線の代わりに平面 で近似できる。この場合、
で近似できる。この場合、

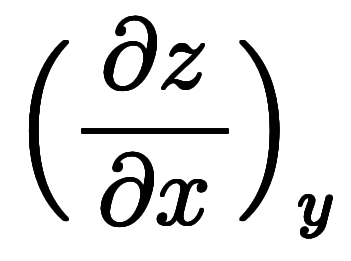 、
、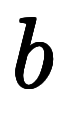

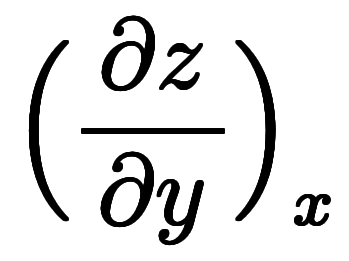 となる。
となる。
ここで、近似平面は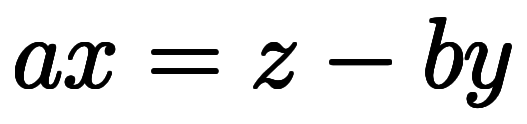 に変形できるため、
に変形できるため、![\ppd{x}{y} = \iro[ak]{-} \ffd{b}{a} $$ \ppd{x}{y} = \iro[ak]{-} \ffd{b}{a} $$](./eq/eq-ni-b3cecd119945346ffb89cb505b2dbea9.png) が得られる。
が得られる。 と
と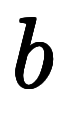 を代入すると、
を代入すると、![\Big( \ppd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{z}{y} \Big)_x}{\Big( \ppd{z}{x} \Big)_y} $$ \Big( \ppd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{z}{y} \Big)_x}{\Big( \ppd{z}{x} \Big)_y} $$](./eq/eq-ni-4df4bc79356d79436861399e56bb5cad.png) になる。
になる。
したがって、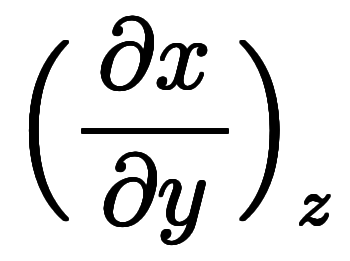 に
に

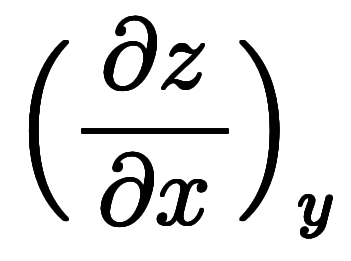 と
と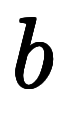

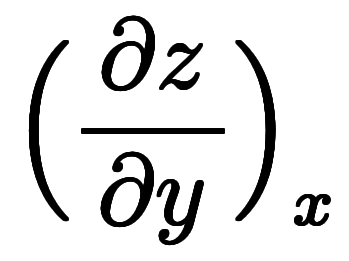 を掛け合わせると、大きさが打ち消して
を掛け合わせると、大きさが打ち消して となり、
となり、![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) が残る。
が残る。





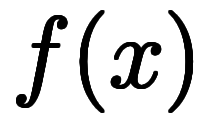 について、
について、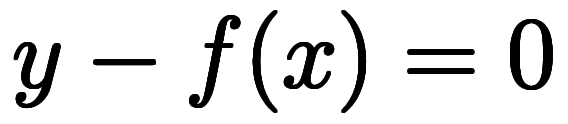 と変形でき、左辺を纏めて
と変形でき、左辺を纏めて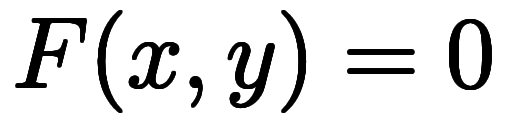 とおける。この関係では、
とおける。この関係では、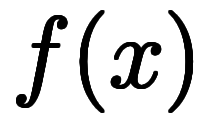 が陽関数、
が陽関数、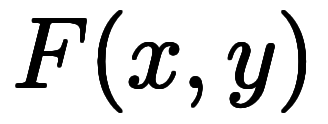 が陰関数と呼ばれる。式の見た目では、陽関数は1つの変数を特別扱いするのに対し、陰関数では全ての変数について対称的な表記になっている。
が陰関数と呼ばれる。式の見た目では、陽関数は1つの変数を特別扱いするのに対し、陰関数では全ての変数について対称的な表記になっている。
陰関数で考える場合、1変数関数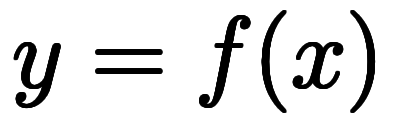 に対する陰関数
に対する陰関数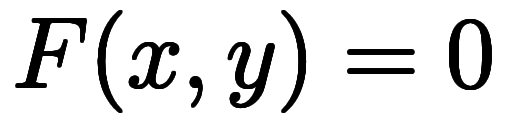 は
は で近似することになる。その結果、
で近似することになる。その結果、

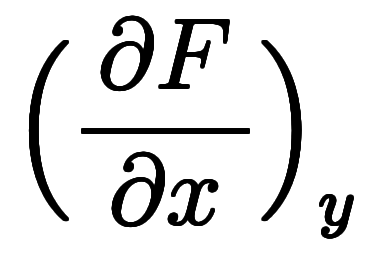 、
、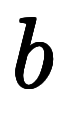

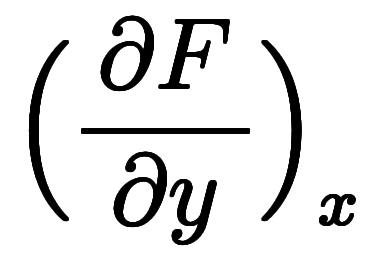 となり、
となり、![\ddd{x}{y} = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_y}{\Big( \ppd{F}{y} \Big)_x} $$ \ddd{x}{y} = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_y}{\Big( \ppd{F}{y} \Big)_x} $$](./eq/eq-ni-73149caaaab3136de54ba520edc1acc7.png) になる。
になる。
同様に、2変数関数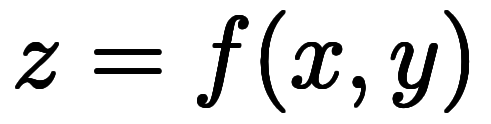 に対する陰関数
に対する陰関数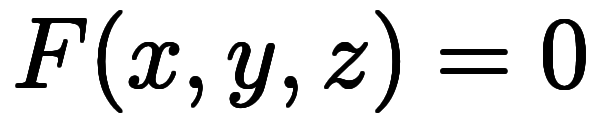 の場合は
の場合は で近似することになる。
で近似することになる。
その結果、

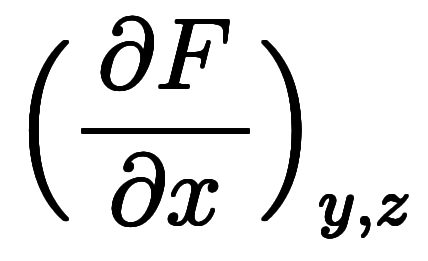 、
、

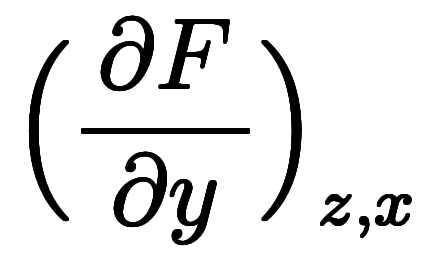 、
、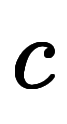

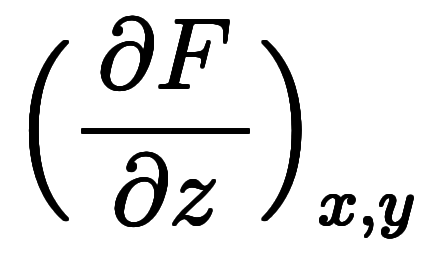 となり、
となり、
![\Big( \ddd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_{y,z}}{\Big( \ppd{F}{y} \Big)_{z,x}} $$ \Big( \ddd{x}{y} \Big)_z = \iro[ak]{-} \ffd{\Big( \ppd{F}{x} \Big)_{y,z}}{\Big( \ppd{F}{y} \Big)_{z,x}} $$](./eq/eq-ni-a48e6ba23d0b37af240faad740f4b120.png) 、
、![\Big( \ddd{y}{z} \Big)_x = \iro[ak]{-} \ffd{\Big( \ppd{F}{y} \Big)_{z,x}}{\Big( \ppd{F}{z} \Big)_{x,y}} $$ \Big( \ddd{y}{z} \Big)_x = \iro[ak]{-} \ffd{\Big( \ppd{F}{y} \Big)_{z,x}}{\Big( \ppd{F}{z} \Big)_{x,y}} $$](./eq/eq-ni-14c260a3d086fedc69053cff5bcc028c.png) 、
、![\Big( \ddd{z}{x} \Big)_y = \iro[ak]{-} \ffd{\Big( \ppd{F}{z} \Big)_{x,y}}{\Big( \ppd{F}{x} \Big)_{y,z}} $$ \Big( \ddd{z}{x} \Big)_y = \iro[ak]{-} \ffd{\Big( \ppd{F}{z} \Big)_{x,y}}{\Big( \ppd{F}{x} \Big)_{y,z}} $$](./eq/eq-ni-058c51a929256e9ac002b875cda2a8ee.png) になる。
になる。
したがって、3つの偏微分を掛け合わせると、大きさが打ち消して となり、
となり、![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) が残る。
が残る。



(1) は陽関数、(2)は陰関数で考えてきた。
ポイントは、(1)と(2)における「![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) 」の現れるタイミングである。
」の現れるタイミングである。
陽関数の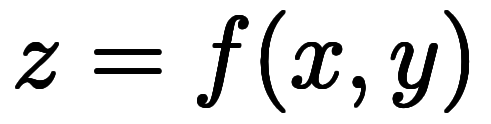 も、陰関数の
も、陰関数の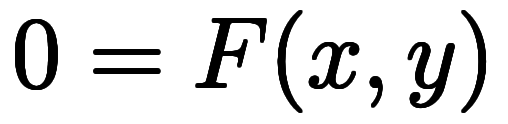 も、ある意味では同じ形をしている。ここでの陰陽とは関数値を変数として扱うかどうかの違いである。そこで、
も、ある意味では同じ形をしている。ここでの陰陽とは関数値を変数として扱うかどうかの違いである。そこで、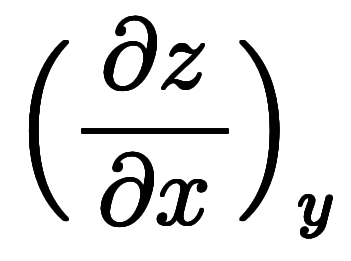

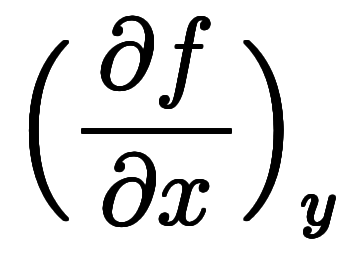 や
や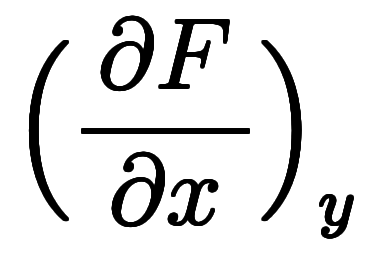 のように関数値を含む微分を「陽的な傾き」と、
のように関数値を含む微分を「陽的な傾き」と、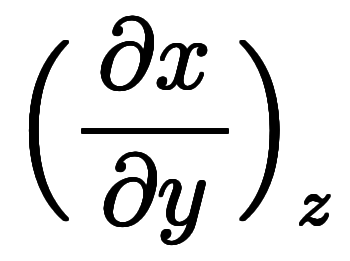 や
や のように独立変数間の微分を「陰的な傾き」と、直感的に捕らえられる。
のように独立変数間の微分を「陰的な傾き」と、直感的に捕らえられる。
そうすると、まず、陽的傾きは形式的にプラスの式になる。これが一般的な傾きの感覚に一致する。
次に、陰的な傾きは形式的にマイナスの式になる。この感覚があれば、オイラーの連鎖式は直感的に理解できるようになる。
纏めて、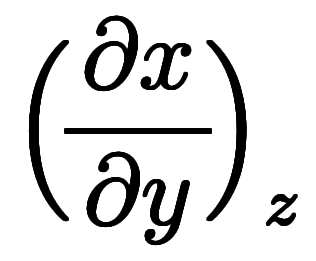
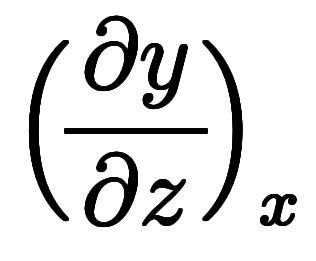
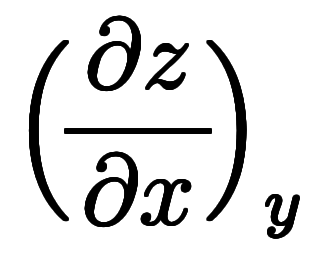 の意味は、
の意味は、
 」になる。
」になる。![\iro[ak]{-} $$ \iro[ak]{-} $$](./eq/eq-ni-0529e03551348a9ba964627e653586ad.png) 」が残る。
」が残る。




 =
= ![\iro[rd]{-} 1 $$ \iro[rd]{-} 1 $$](./eq/eq-ni-a10b2d1aeb02af40fb87db0dfe057bf4.png) ⇒
⇒ ![\Big(\! \iro[rd]{-} \ffd{a}{b} \!\Big) $$ \Big(\! \iro[rd]{-} \ffd{a}{b} \!\Big) $$](./eq/eq-ni-8caa482e2606f4e05c615872b6f9d9bc.png)
![\Big(\! \iro[rd]{-} \ffd{b}{c} \!\Big) $$ \Big(\! \iro[rd]{-} \ffd{b}{c} \!\Big) $$](./eq/eq-ni-6b8a746d29308d50bb36ef446d06488f.png)
![\Big(\! \iro[rd]{-} \ffd{c}{a} \!\Big) $$ \Big(\! \iro[rd]{-} \ffd{c}{a} \!\Big) $$](./eq/eq-ni-5bb4eed822b23f304f4ee12dbacf273f.png) =
= ![\iro[rd]{-} 1 $$ \iro[rd]{-} 1 $$](./eq/eq-ni-a10b2d1aeb02af40fb87db0dfe057bf4.png)