![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル三重積公式 のバックアップ(No.6) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル三重積公式 のバックアップ(No.6) |
|
| File not found: "Ax(BxC).01.png" at page "ベクトル三重積公式"[添付] | File not found: "Ax(BxC).02.png" at page "ベクトル三重積公式"[添付] |
まず、 は
は と
と の両方と垂直である。言い換えれば、
の両方と垂直である。言い換えれば、 は
は と
と を含む面と垂直で、その法線ベクトルである。
を含む面と垂直で、その法線ベクトルである。
同様に、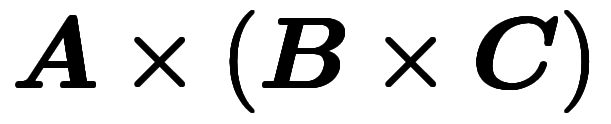 は
は と
と の両方と垂直である。このうち、
の両方と垂直である。このうち、 と垂直であるため、面の法線ベクトルと垂直なベクトルということで、その面に平行する(=含まれる)ことになる。
と垂直であるため、面の法線ベクトルと垂直なベクトルということで、その面に平行する(=含まれる)ことになる。
よって、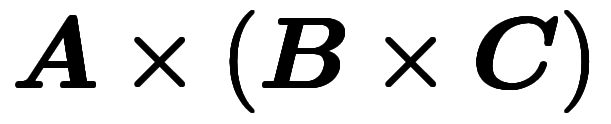 は、
は、 と
と と同一平面上にある。
と同一平面上にある。



この性質のため、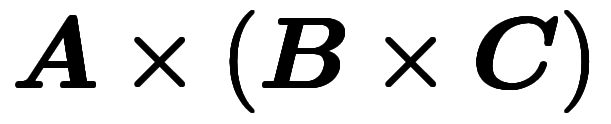 を
を 、
、 の一次結合で書ける:
の一次結合で書ける:
|
これに対し、 にはスカラの係数を、
にはスカラの係数を、 には
には か
か のどちらかを入れる。また、この時点で、式の両辺において、
のどちらかを入れる。また、この時点で、式の両辺において、 と
と が同順であることに注意。
が同順であることに注意。



まずは、右辺の第1項
 に注目する。左辺にある材料は
に注目する。左辺にある材料は 、
、 、
、 。この項では
。この項では が既に使われているため、残っている
が既に使われているため、残っている と
と でスカラの係数を簡単に作ることを考えれば良い。
でスカラの係数を簡単に作ることを考えれば良い。
2つのベクトルからスカラを作る方法で最も簡単な演算と言えば ── 内積。というわけで、答えが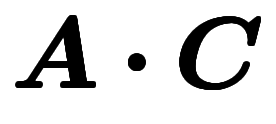 が入る。同様に、
が入る。同様に、
 では、
では、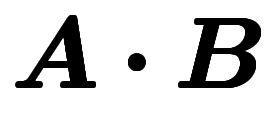 が入る。
が入る。
よって、
|





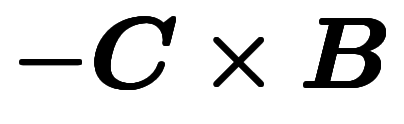 のため、右辺も
のため、右辺も と
と を入れ替えたらマイナスにならねばならない。
を入れ替えたらマイナスにならねばならない。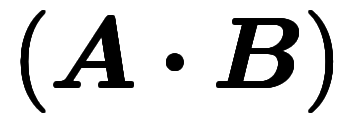
 で
で と
と を入れ替えたら
を入れ替えたら
 になるため、
になるため、 には「
には「 」を入れねばならなくなる。
」を入れねばならなくなる。
もしくは、外積が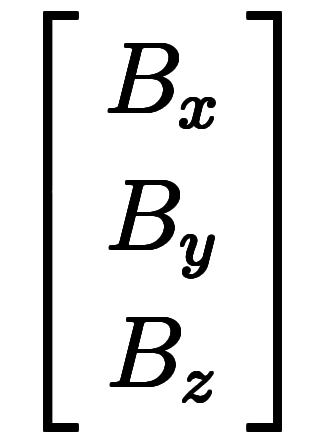

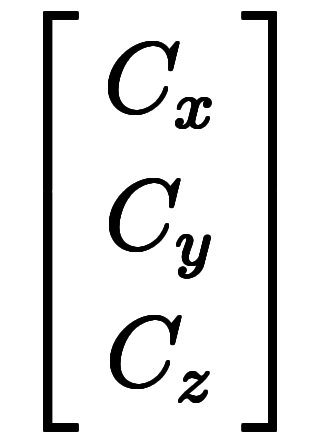

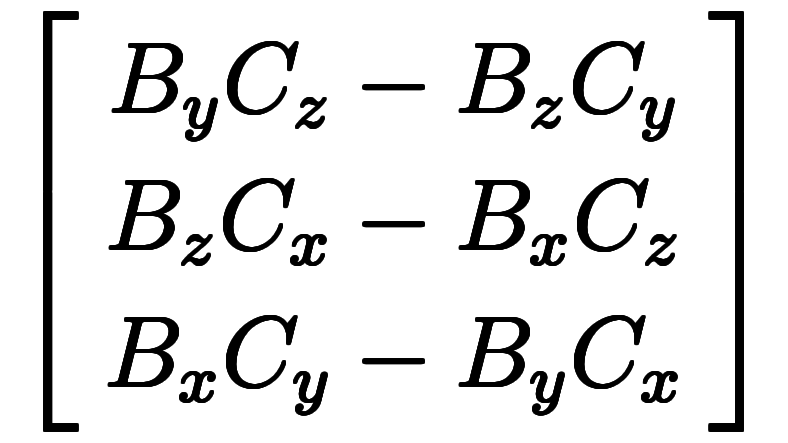 で計算されるように、「積−積」の形が基本と言える。そのセンスで
で計算されるように、「積−積」の形が基本と言える。そのセンスで に「
に「 」を入れても良い。
」を入れても良い。
よって、
|



上記とは別に、3次元問題を等価変換で2次元問題に落として簡単化する方法もある。
| File not found: "Ax(BxC).03.png" at page "ベクトル三重積公式"[添付] | File not found: "Ax(BxC).04.png" at page "ベクトル三重積公式"[添付] |
ここで利用するのは、外積の同値条件である。外積の幾何的意味は、2つのベクトルの張る平方四辺形の面積であるため、片方を固定しても、面積さえ変わらなければ、他方を自由に動かせる。例えば上の図の場合、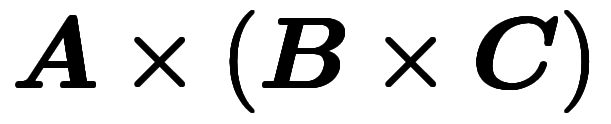

 が成り立つ。
が成り立つ。
また、 は特別に、
は特別に、 と垂直なベクトルを選んでいるが、このようなベクトルはタダ一つに決まる。そして、
と垂直なベクトルを選んでいるが、このようなベクトルはタダ一つに決まる。そして、 は
は と垂直なため、
と垂直なため、 や
や と同一の平面に属する。
と同一の平面に属する。
同様に、 において、
において、 を固定すれば、
を固定すれば、 に垂直な
に垂直な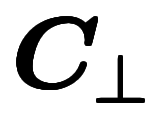 をタダ一つ決まる。ここでも、
をタダ一つ決まる。ここでも、 が
が や
や と同一の平面に属する。
と同一の平面に属する。
よって、 では、全てのベクトルが同一平面上にあり、右図の2次元の問題となる。
では、全てのベクトルが同一平面上にあり、右図の2次元の問題となる。