![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル三重積公式 のバックアップ(No.9) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル三重積公式 のバックアップ(No.9) |
凌宮組立術: |
|
ここで、 にはスカラの係数が、
にはスカラの係数が、 には「
には「 」または「
」または「 」の符号が入る。
」の符号が入る。



次は、![\iro[ak]{\:A \vx (\:B \vx \:C)} $$ \iro[ak]{\:A \vx (\:B \vx \:C)} $$](./eq/eq-ni-f64b8dd6420f70a6f0949b05012ecd78.png) が3つの文字の掛け算であるため、次元は掛け算の種類を問わず、
が3つの文字の掛け算であるため、次元は掛け算の種類を問わず、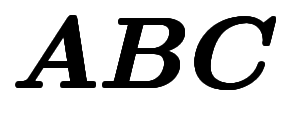 の次元である*2。
の次元である*2。
よって、
![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) も
も
![\iro[md]{\:C} $$ \iro[md]{\:C} $$](./eq/eq-ni-04479ec979ee31daa4246a3ac337662c.png) も3文字の掛け算であるべき。
も3文字の掛け算であるべき。
|
さらに、係数はスカラ値である必要があるため、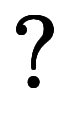 は自ずと内積になる*3。
は自ずと内積になる*3。
|
 が[m]、
が[m]、 が[s]、
が[s]、 が[g]とか。
が[g]とか。


外積の交代性で

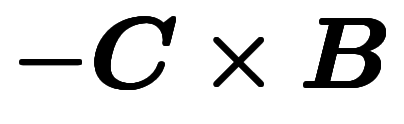 であるため、右辺も
であるため、右辺も と
と が交代したらマイナスになる。
が交代したらマイナスになる。
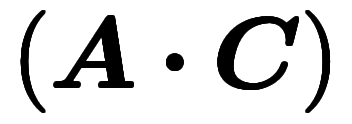
 で
で と
と が交代したら
が交代したら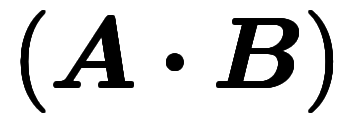
 になるため、交代則を成立させるには、2つの
になるため、交代則を成立させるには、2つの には「+」と「−」と逆の符号が入る。
には「+」と「−」と逆の符号が入る。
問題は、左辺は2つの書き方があり、掛け方によって符号が逆転する。
|
|
|
|
|
|
この符号は外積の回転方向を2回も考える必要がある。
3次元空間でぐるぐる回るのは結構面倒なので、便宜的な手法ではあるが2次元で済ませたい。
さらに、三重積は任意のベクトルで成立するため、次の2つの条件を満たす単純な例で済ませたい。
論はないが証拠、これで(片方の)符号が分る:
![\iro[ao]{\:A} \vx (\iro[md]{\:B} \vx \iro[md]{\:C}) $$ \iro[ao]{\:A} \vx (\iro[md]{\:B} \vx \iro[md]{\:C}) $$](./eq/eq-ni-958bee55dc5281e2ef2d26a4af3c750c.png) について、まず
について、まず![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) に
に![\iro[md]{\:C} $$ \iro[md]{\:C} $$](./eq/eq-ni-04479ec979ee31daa4246a3ac337662c.png) を右から掛けて、
を右から掛けて、![\iro[ao]{\:A} $$ \iro[ao]{\:A} $$](./eq/eq-ni-43c935b28da372b2dda0aeb6cc6ff68e.png) を左から掛ける。
を左から掛ける。
ポイントは掛ける向きが逆であるため、向きが打ち消して元の![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) の向きになる。
の向きになる。
したがって、![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) の符号は「
の符号は「 」になり、残る
」になり、残る![\iro[md]{\:C} $$ \iro[md]{\:C} $$](./eq/eq-ni-04479ec979ee31daa4246a3ac337662c.png) には逆の「
には逆の「 」が付く。
」が付く。
|
|
![(\iro[md]{\:A} \vx \iro[md]{\:B}) \vx \iro[ao]{\:C} $$ (\iro[md]{\:A} \vx \iro[md]{\:B}) \vx \iro[ao]{\:C} $$](./eq/eq-ni-619f26f5c7e608e26bedc1179f23a913.png) について、まず
について、まず![\iro[md]{\:A} $$ \iro[md]{\:A} $$](./eq/eq-ni-09866d1ea5751ff6998ebf8301a74f63.png) に
に![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) を右から掛けて、
を右から掛けて、![\iro[ao]{\:C} $$ \iro[ao]{\:C} $$](./eq/eq-ni-5549b3bc65e0560d112fda5cdc4df64b.png) をさらに右から掛ける。
をさらに右から掛ける。
ポイントは掛ける向きが同じであるため、そのまま回し続けて![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) と逆の向きになる。
と逆の向きになる。
したがって、![\iro[md]{\:A} $$ \iro[md]{\:A} $$](./eq/eq-ni-09866d1ea5751ff6998ebf8301a74f63.png) の符号は「
の符号は「 」になり、残る
」になり、残る![\iro[md]{\:B} $$ \iro[md]{\:B} $$](./eq/eq-ni-9902f15593cf579275415d39a42ac21d.png) には逆の「
には逆の「 」が付く。
」が付く。
|
|