![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル積分の変数変換係数 のバックアップ(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル積分の変数変換係数 のバックアップ(No.3) |
凌宮表記術: |
|



 on
on  : 1次元空間上の線積分
: 1次元空間上の線積分 


一般に、1次元から1次元の変数変換は常微分で表される。
|
凌宮表記では全く同じ表記になる。
他の具体例に揃えてベクトル表記で書くと、

 、
、

 として、
として、
|
 on
on 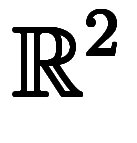 : 2次元空間上の面積分
: 2次元空間上の面積分 


高次元での線積分では、成分ごとに変数変換すれば良い。
|
凌宮表記では、変換係数を正基底と逆基底の外積から導出できる。


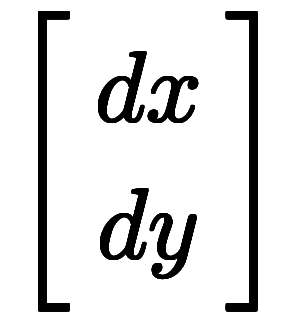 、
、

 として、
として、
|
|
 on
on 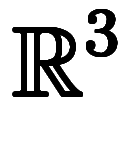 : 3次元空間上の面積分
: 3次元空間上の面積分 


3次元は2次元と同様に考えれば良い。
|
凌宮の導出も同様に、

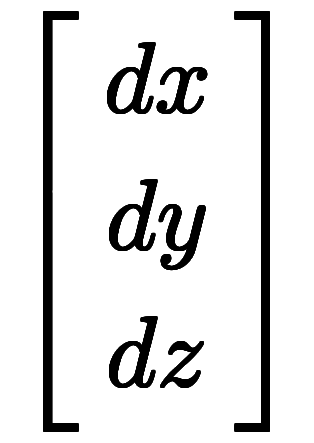 、
、

 として、
として、
|
|
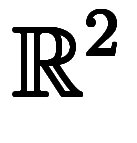 on
on 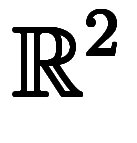 : 2次元空間上の面積分
: 2次元空間上の面積分 


一般に、2次元から2次元の変数変換は微小平方四辺形の面積の比となる。


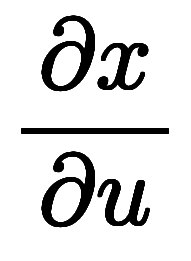


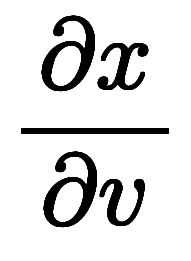
 、
、

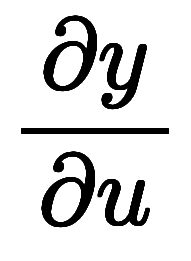



 であるため、
であるため、
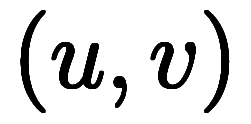 座標上では、
座標上では、 と
と が平方四辺形を張り、面積は
が平方四辺形を張り、面積は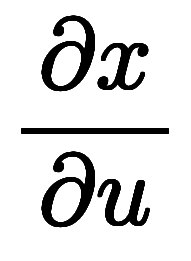


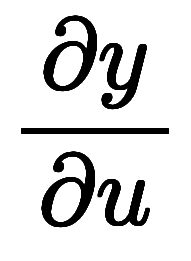
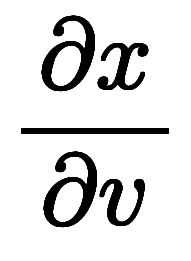 。
。
よって、
|
この変換係数には、変換元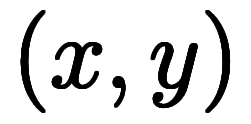 の変換先
の変換先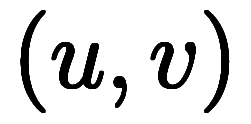 に対する偏微分の全組み合わせが出揃っていて、
に対する偏微分の全組み合わせが出揃っていて、
これらを成分に持つヤコビ行列の行列式でも表現できる。
ヤコビ行列: |
ヤコビアン: |
|
対して、凌宮表記では外積から導かれる。



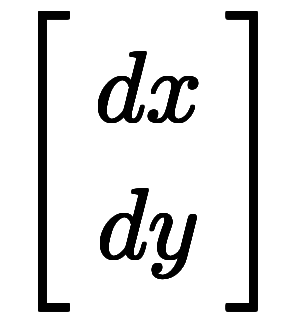 、
、

 として、
として、
変形の途中で現れる2次元のクロス積はあまり広く使われてないが、
3次元空間上の2次元曲面の変換係数がヤコビアンで表せず、クロス積を使う事態を考えると、
2次元空間上の変換係数もクロス積で解釈できた方が整理しやすい。