![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
ベクトル積分の変数変換係数 |
凌宮表記術: |
|



ベクトル積分は、考えている空間の次元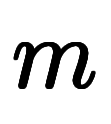 と積分領域の次元
と積分領域の次元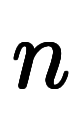 により分類できる。
により分類できる。
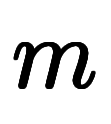 と
と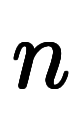 は共に正自然数であり、
は共に正自然数であり、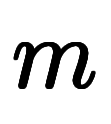

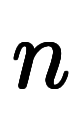 の関係にあるため、
の関係にあるため、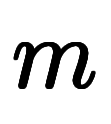 次元空間内では
次元空間内では 通りに分かれる。
通りに分かれる。
例えば、3次元までのベクトル解析では、以下の6通りになる。
on  1次元空間上の 線上の | on  2次元空間上の 面上の | on 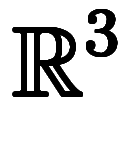 3次元空間上の 体上の(胞上の) | |
|---|---|---|---|
 1次元積分 線積分 |  on on  1次元空間上の1次元積分 線上の線積分 |  on on 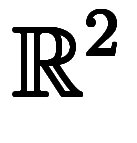 2次元空間上の1次元積分 面上の線積分 |  on on 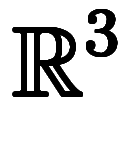 3次元空間上の1次元積分 体上の線積分 |
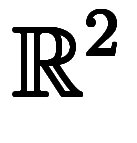 2次元積分 面積分 | 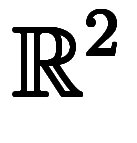 on on 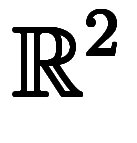 2次元空間上の2次元積分 面上の面積分 | 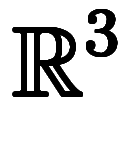 on on 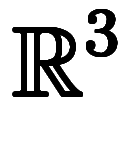 3次元空間上の2次元積分 体上の面積分 | |
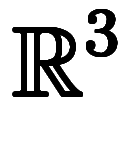 3次元積分 体積分 | 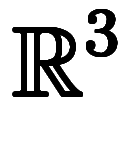 on on 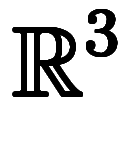 3次元空間上の1次元積分 体上の体積分 |
以下では、ベクトル解析学の知見に基づき、各場合に対し変換係数を個別に定義する。
 on
on  : 1次元空間上の線積分
: 1次元空間上の線積分 


一般に、1次元から1次元の変数変換は常微分で表される。
|
凌宮表記では、同じ表記に定義する。
統一表記で書くと、

 、
、

 であり、
であり、
|
 on
on 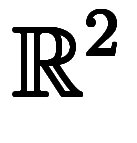 : 2次元空間上の面積分
: 2次元空間上の面積分 


高次元での線積分では、成分毎に1次元の変数変換を行えば良い。
変換先が1次元のため、 と
と は
は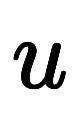 のみの関数であり、
のみの関数であり、
変換係数は常微分、つまり1変数関数の微分になる*1。
|
凌宮表記では、変換係数を正基底と逆基底のテンソル積として定義する。


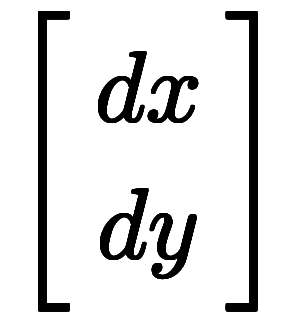 、
、

 として、
として、
|
|
 on
on 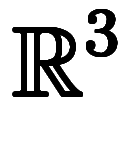 : 3次元空間上の面積分
: 3次元空間上の面積分 


3次元は2次元と同様に考えれば良い。
|
凌宮の表記は2次元と同様に、

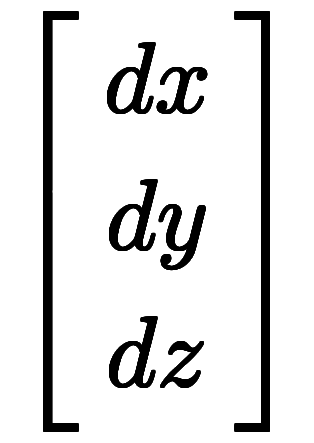 、
、

 として、
として、
|
|
 on
on  : 2次元空間上の面積分
: 2次元空間上の面積分 


一般に、2次元から2次元の変数変換は微小平行四辺形の面積比となる。


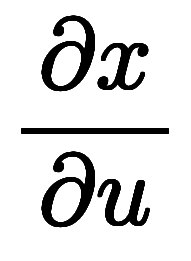


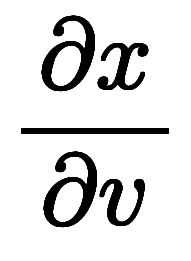
 、
、

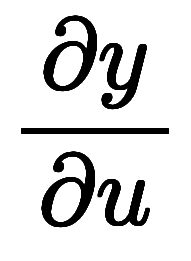



 であるため、
であるため、
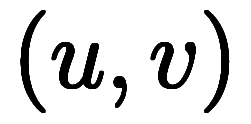 座標上では、
座標上では、 と
と が平行四辺形を張り、面積は
が平行四辺形を張り、面積は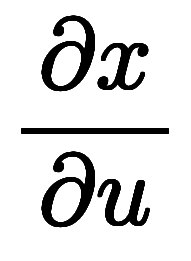


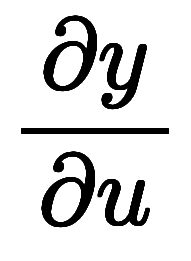
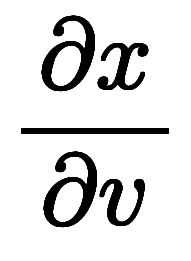 。
。
よって、
|
この変換係数には、変換元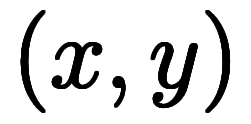 の変換先
の変換先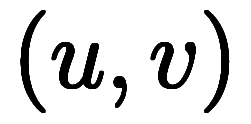 に対する偏微分の全組み合わせが出揃っていて、
に対する偏微分の全組み合わせが出揃っていて、
これらを成分に持つヤコビ行列の行列式でも表現できる。
ヤコビ行列: |
ヤコビアン: |
|
この他、あまり用いられないものの、2次元のベクトルのクロス積を用いた表現もある。
3次元空間上の面積分との一貫性の観点では、クロス積表記の方が優れている。
|
凌宮表記では、まず1次元ヤコビアンをテンソル積として定義し、
次に



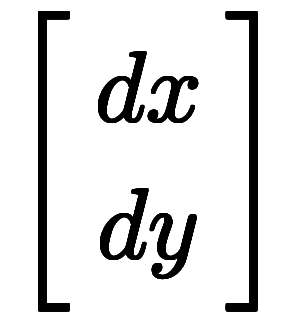 、
、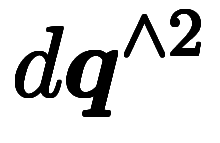

 の表記に合わせて、
の表記に合わせて、
1次のヤコビアンから2次のヤコビアンに変換する演算「 」をクロス積で形式的に定義する。
」をクロス積で形式的に定義する。
|
|
|
変形の途中で現れる2次元のクロス積はあまり広く使われてないが、
3次元空間上の2次元曲面の変換係数がヤコビアンで表せず、クロス積を使う事態を考えると、
2次元空間上の変換係数もクロス積で解釈できた方が整理しやすい。
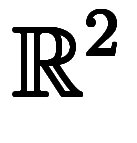 on
on 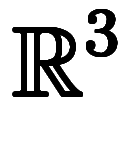 : 3次元空間上の面積分
: 3次元空間上の面積分 


高次元での面積分では、線積分と同様に成分ごとに変数変換すれば良い。
|
3×2のヤコビ行列自体は定義されているが、正方行列でないため行列式が定義されていないため、
ヤコビアンを用いた変換係数の表記法はこれ以上簡潔にできない。
ヤコビ行列: |
ところで、2x2のヤコビアンを展開すると、交差積になっているに気づく。
そのため、クロス積で簡潔に記述手法が広く用いられている。
|
凌宮表記では、2次元空間上の面積分と同様に、
1次のヤコビアンを定義してからクロス積で2次のヤコビアンを形式的に定義する。




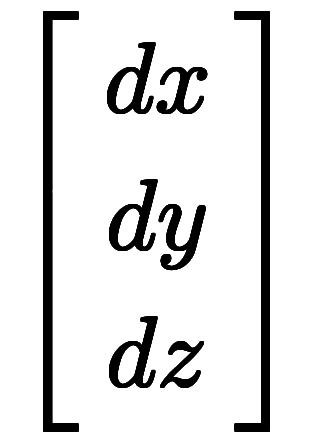 、
、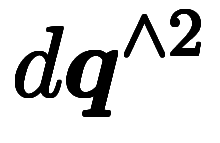

 として、
として、
|
|
|
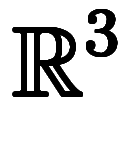 on
on 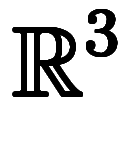 : 3次元空間上の体積分
: 3次元空間上の体積分 


一般に、3次元から3次元の変数変換は微小平行六面体の体積比となる。


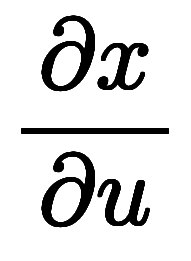


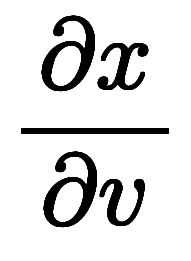


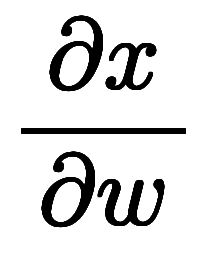
 、
、


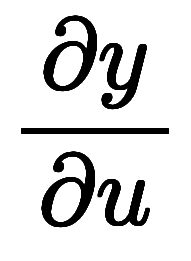






 、
、


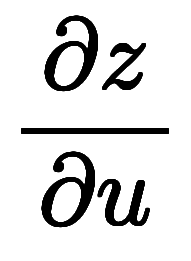


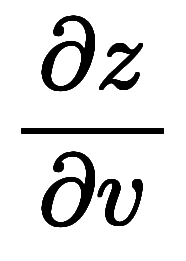


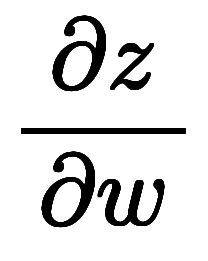
 、であるため、
、であるため、
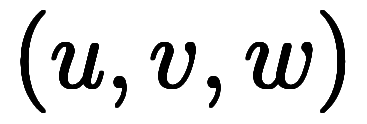 座標上では、
座標上では、 ,
, ,
, が平行六面体を張り、
が平行六面体を張り、
体積はヤコビアンまたはベクトルのスカラ三重積で表せる。
|
ヤコビ行列: |
ヤコビアン: |
|
凌宮表記では、3次元空間上の面積分を真似て、
1次のヤコビアンを定義してからスカラ三重積で2次のヤコビアンを形式的に定義する。




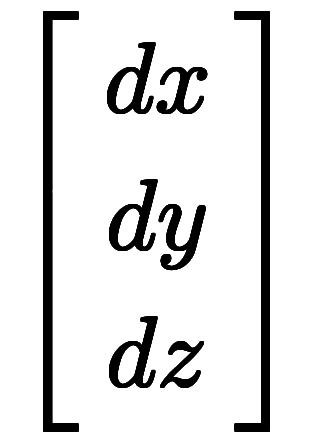 、
、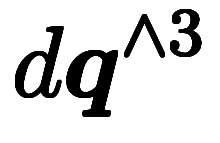

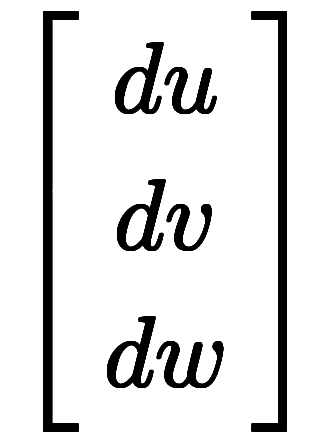 として、
として、
|
|
|



以下に、表記毎に纏める。
3次元のベクトル解析で扱う空間と積分は以下の6通り。



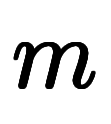 次元空間上の
次元空間上の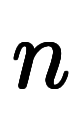 次元積分:
次元積分: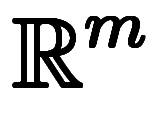 on
on 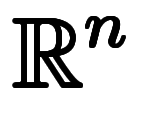 では、
では、
統一的に
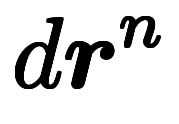



 で表せる。
で表せる。
on  | on  | on 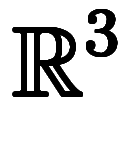 | |
|---|---|---|---|
 | 1次元空間上の1次元積分 線上の線積分 | 2次元空間上の1次元積分 面上の線積分 | 3次元空間上の1次元積分 体上の線積分 |
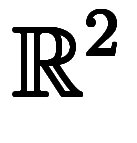 | 2次元空間上の2次元積分 面上の面積分 | 3次元空間上の2次元積分 体上の面積分 | |
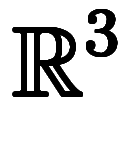 | 3次元空間上の3次元積分 体上の体積分 |