![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
複素数の双対基底(編集中)(ネタ) |
複素数の基底表記 |
|
|
|
|



逆基底を正基底の線形結合で表し*2、正基底と内積を取れば正基底と逆基底の関係が求まる。
|
|
と置けば、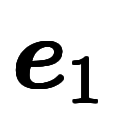

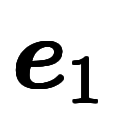

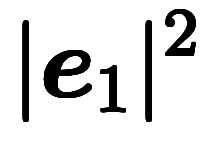

 、
、





 、直交なために
、直交なために



 より、
より、
|
|
|
|
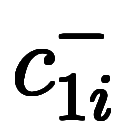
よって、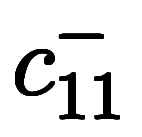

 、
、

 、
、

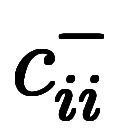
 、
、

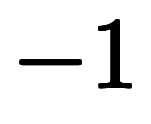 となり、
となり、
ここで、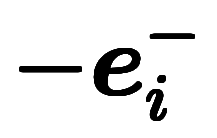

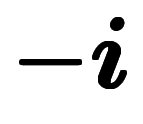 は負の正規条件を満たすが、
は負の正規条件を満たすが、

 を
を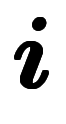 で表記すると
で表記すると

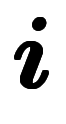

 となり、
となり、
通常の複素数積である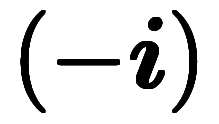


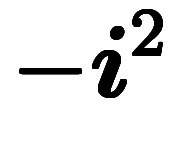

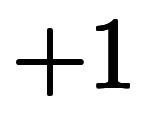 と異なって、少々紛らわしい。
と異なって、少々紛らわしい。
内積に関して、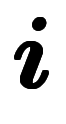 が単位ベクトルで、
が単位ベクトルで、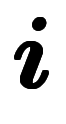 自身と向きが同じであるため、
自身と向きが同じであるため、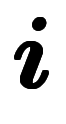

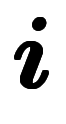

 となる。
となる。
このため、内積と複素数積の違いに十分気をつける必要がある。



任意の複素数




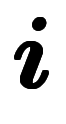 は、
は、
正基底と逆基底を使って

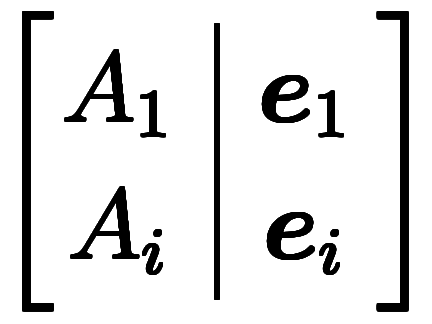

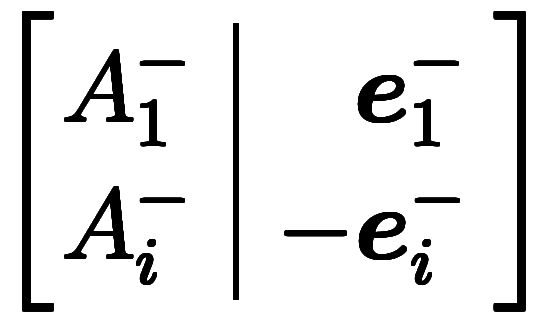 と書ける*4。
と書ける*4。
 と
と で表すと、
で表すと、

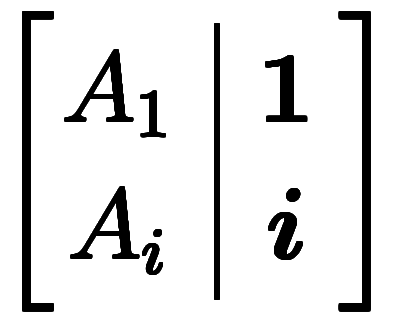

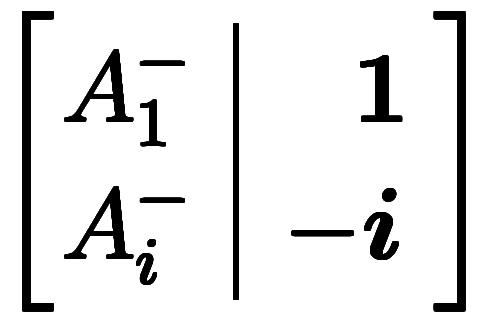 になる。
になる。
これを任意の に対する基底
に対する基底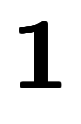 と
と の恒等式と見なせば、正基底と逆基底の成分間の関係が得られる。
の恒等式と見なせば、正基底と逆基底の成分間の関係が得られる。
| |
正基底と逆基底で表された の内積を取ると、長さの二乗
の内積を取ると、長さの二乗



 が得られる。
が得られる。
|
ところで、複素数解析では、 を共役素数
を共役素数




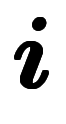 を使って表現する場合が多い。
を使って表現する場合が多い。
|