![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
定数係数4階線形常微分方程式 |
|
|
| |
⇔ | 式1: 線形常微分演算子化 |
⇔ | 式2: 線形常微分演算子の因数分解 |
⇔ | 式3: 逆演算子表記 |
⇔ | 式4: 逆演算子を積分に置換*1 |
⇔ | 式5: 4回の逐次積分 |
以下からは具体的な積分計算が始まる。 は全て積分定数。
は全て積分定数。
|
|
|
|
|
|
|
|
|
|


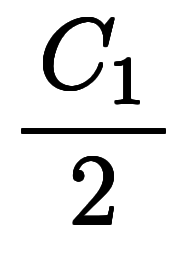 、
、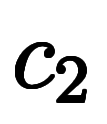

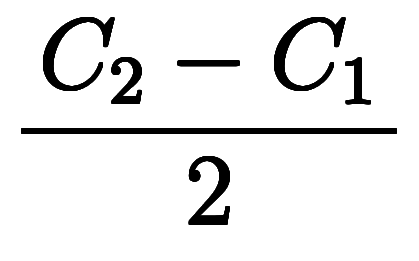 、
、

 、
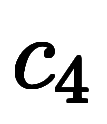
、

 と置けば、複素係数での解集合が得られる。
と置けば、複素係数での解集合が得られる。
| 複素関数解 |
さらに解集合を実係数に限定したければ、
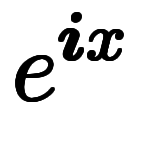


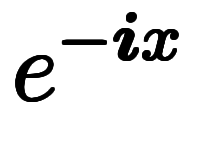 を三角関数で表示してから係数を制限すれば良い。
を三角関数で表示してから係数を制限すれば良い。
改めて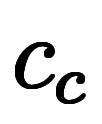



 、
、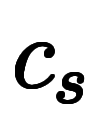

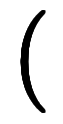



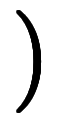
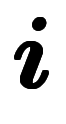 と置いた上で、係数を全て実数に限れば、実数係数での解集合になる。
と置いた上で、係数を全て実数に限れば、実数係数での解集合になる。
| 実関数解 |



|
より、
|
|
|
|
与式の左辺に代入すると、
|
|
|
|
変数に依らずに右辺に一致するため、得られた解は全て与式を満たす。



演算子法では線形常微分の因子と解の基底の対応関係から、2階の定数係数常微分方程式の知見を4階の方程式に流用できることが知られている。斉次方程式の一般解は基底と積分定数の線形結合に相当し、特殊解は積分定数を無視した残りの部分に相当する。
具体に、斉次方程式










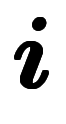



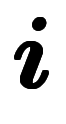


![y_{\iro[red]*} = $$ y_{\iro[red]*} = $$](./eq/eq-ni-2fb24d74da4c3e521680f441a30f9158.png)
![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) に関して、
に関して、




 を持つため、一般解に基底
を持つため、一般解に基底 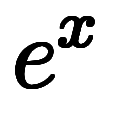 の項を持つ。
の項を持つ。



 を持つため、一般解に基底
を持つため、一般解に基底
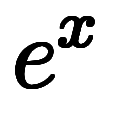 の項を持つ。
の項を持つ。


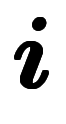



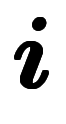
 を持つため、一般解に基底
を持つため、一般解に基底 
 と
と
 の項を持つ。
の項を持つ。このため、微分方程式を因数分解できた時点で、斉次方程式の一般解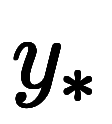 が直ちに分かる。
が直ちに分かる。
⇒ |
積分定数は一般解で考慮しているため、残る特殊解 は積分定数を無視した不定積分で済ませられる。
は積分定数を無視した不定積分で済ませられる。
| |
| |
| |
| |
|
もしくは、特殊解は右辺を基底とする項を持つ事実を利用し、


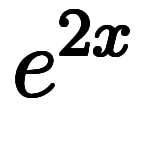 と置いて非斉次方程式に放り込んでも特殊解が決まる。
と置いて非斉次方程式に放り込んでも特殊解が決まる。
| |
| 検算と同じ計算 |
| |
| |
|
これより非斉次方程式の一般解 を、特殊解
を、特殊解 と斉次方程式の一般解
と斉次方程式の一般解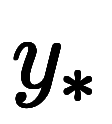 の和として作り出す。
の和として作り出す。
|