凌宮読取術: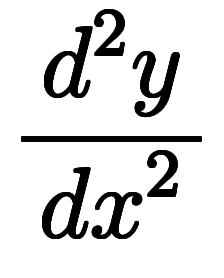

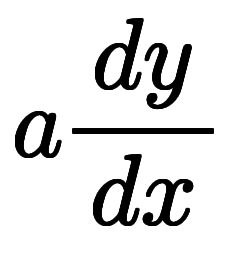

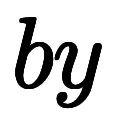

 ⇒
⇒ 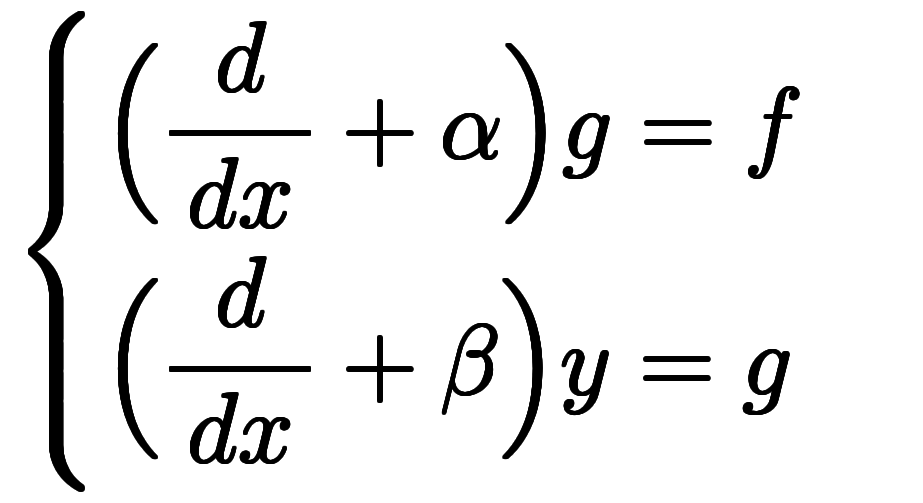



定数係数の2階線形常微分方程式は運動力学や電磁気学で支配方程式として現れるため、
「特性方程式*1&定数変化法*2」または、「特性方程式*3&未定係数法*4」など、
いわゆる定番な解法が大学入学早々叩き込まれる。
問題は、この方法は「解のパターンが分かる前提で答えを組み立てる」手法であること*5、
および、場合分けが複雑で一から覚える知識が多いことで、消化不良となりやすい。
一応それぞれの背後には大きな理論があるものの、短時間に習得できるものではない。
これに対し、凌宮数学では、高校で習う因数分解を利用して微分方程式を分解し、
直前に習うはずの1階線形常微分方程式に還元して解く方法を使う。
|
| |
| |
⇒ 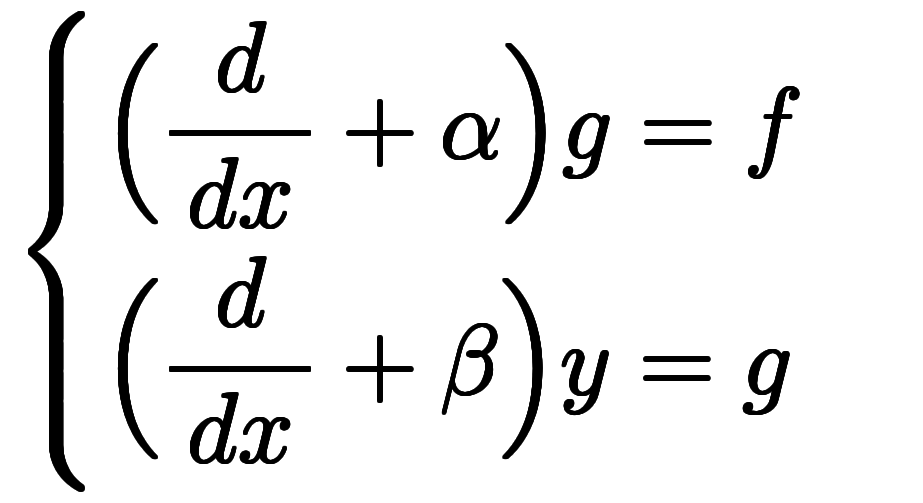 | |
EMANの物理学/物理数学/定数係数2階線形同次微分方程式: http://homepage2.nifty.com/eman/math/differential09.html
EMANの物理学/物理数学/定数係数線形非同次微分方程式: http://homepage2.nifty.com/eman/math/differential11.html
Matsuda's Web Page/(高専生のための)微分方程式解法ノート/2. 簡単な線形微分方程式>http://www.tsuyama-ct.ac.jp/matsuda/d-eq/bi2.pdf
Matsuda's Web Page/(高専生のための)微分方程式解法ノート/3. 線形微分方程式の特殊解の求め方>http://www.tsuyama-ct.ac.jp/matsuda/d-eq/bi3.pdf
反面、これらの手法は積分を飛ばすために非常に速い。テスト対策のみならず、実用の面においても覚えた方が良い。
線形常微分演算の因数分解 


最初の読み替えから演算子部を取り出すと、因数分解した形の式が現れる:
読み替えが可能な理由は常微分の線形性によるが、右側の展開で簡単に確認できる。
逆に言うと、定数と常微分の可換性を利用しているため、 も
も も非定数係数の場合は適応できない。
も非定数係数の場合は適応できない。
連立1階線形常微分方程式 


因数分解形から連立一階形への変形は、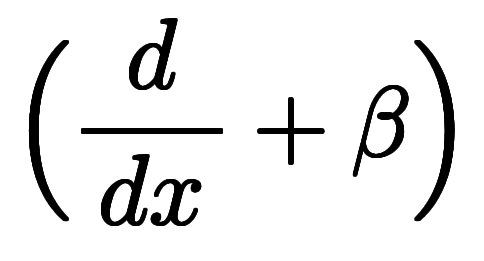
 を
を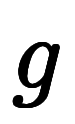 と置いただけである。
と置いただけである。
そうすれば、置き換えられた式も、置く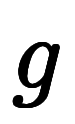 の定義式自体も、自ずと1階線形常微分方程式となる。
の定義式自体も、自ずと1階線形常微分方程式となる。
実際、連立も名ばかりのもので、上の式に が無いため、先に
が無いため、先に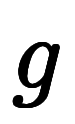 から解けば良い。
から解けば良い。
解の公式 


1階線形常微分の解より、連立した2式の解はそれぞれ次のようになる:
下式を上式に代入して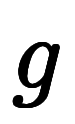 を消せば、解の統一公式が得られる:
を消せば、解の統一公式が得られる:
この公式を解けば、2つの不定積分で計2つの積分定数が現われて2つの基本解を作る。残りの本体が特殊解となる。
定番の解法に対する最大の特徴は、場合分けが一切なく、一本の式に統一されている点である。
このため、定番解法に比べると、覚える内容が激減する。
適応例【執筆中】 


以下に、積和形の公式と定番手法の場合分けの対応例を示す。
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)






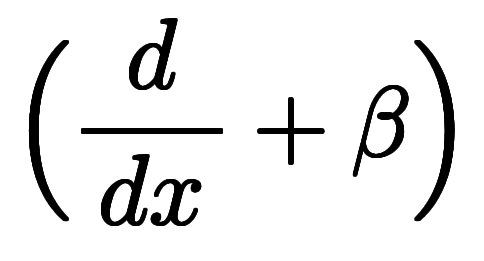
 を
を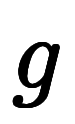 と置いただけである。
と置いただけである。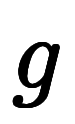 の定義式自体も、自ずと1階線形常微分方程式となる。
の定義式自体も、自ずと1階線形常微分方程式となる。 が無いため、先に
が無いため、先に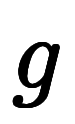 から解けば良い。
から解けば良い。


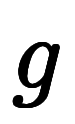 を消せば、解の統一公式が得られる:
を消せば、解の統一公式が得られる:

