![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
温度単位の変換 のバックアップ(No.10) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
温度単位の変換 のバックアップ(No.10) |
温度単位の換算 |
|||||||||||||||||||||||||||
|
この式から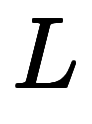 を打消して、分母を払えば、一般的に用いられる
を打消して、分母を払えば、一般的に用いられる


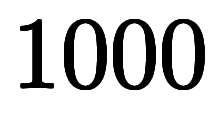
 *2が得られる。
*2が得られる。
温度の場合は

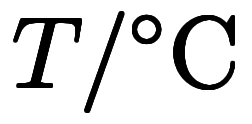 、
、

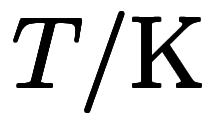 と表記でき*3、温度単位の換算はこうなる:
と表記でき*3、温度単位の換算はこうなる:
|
 、セルシウス温度を
、セルシウス温度を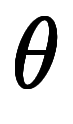 と書き分けているが、同じ温度であるため、凌宮数学では同じ量記号
と書き分けているが、同じ温度であるため、凌宮数学では同じ量記号 に統一している。
に統一している。


一般に、温度と比例関係にある法則を定式化した場合、量の方程式は当然比例式になる。
しかし、数値方程式では、絶対温度 を用いた場合は同形の比例式になるのに対し、
を用いた場合は同形の比例式になるのに対し、
セルシウス温度 を用いた場合は比例式にならず少し複雑な式に化ける。
を用いた場合は比例式にならず少し複雑な式に化ける。
例えば、シャルルの法則では気体の温度 は体積
は体積 に比例し*4、量方程式は比例式になる。
に比例し*4、量方程式は比例式になる。
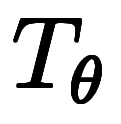

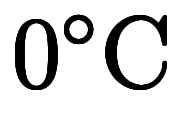 における気体の体積を
における気体の体積を とすると、シャルルの法則は表1にある各式に書けて、
とすると、シャルルの法則は表1にある各式に書けて、
セルシウス温度を用いる場合のみ、温度の項毎に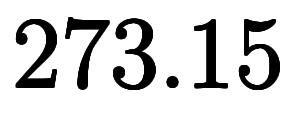 が加わり、比例式で無くなる。
が加わり、比例式で無くなる。
| 表1:シャルルの法則 | ||
|---|---|---|
| 量方程式 |   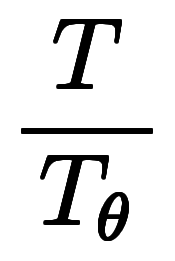 | |
| 数値 方程式 | 絶対 温度 | 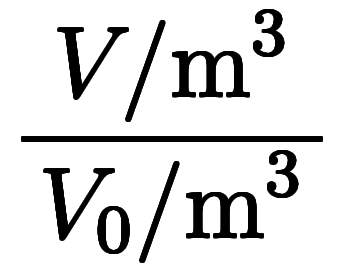  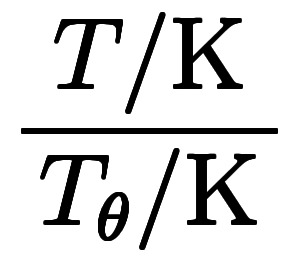 |
| セルシウス 温度 | 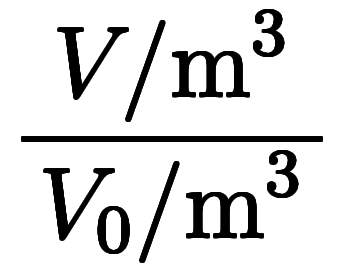    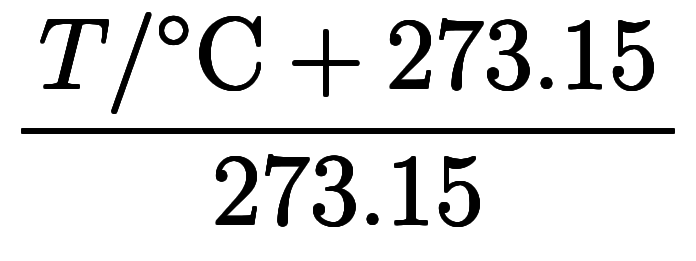 *5 *5 | |



温度を表すセルシウス温度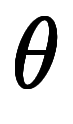 、水の凝固点
、水の凝固点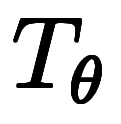

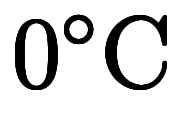 を基準とした相対温度と見なせる。
を基準とした相対温度と見なせる。
同様に、絶対と名乗る絶対温度 も熱力学限界値
も熱力学限界値

 を基準とした相対温度と見なせる。
を基準とした相対温度と見なせる。
この視点では、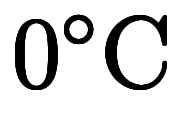 と
と の単位変換は
の単位変換は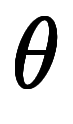 と
と の座標変換に変わる。
の座標変換に変わる。
|
ここに登場する
 は
は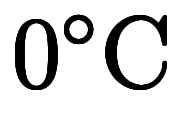 と
と の温度差
の温度差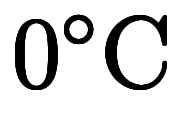

 であり、単位は
であり、単位は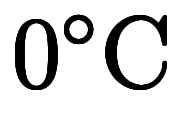 でも
でも でも同じである。
でも同じである。
このように、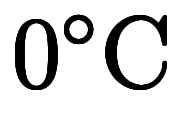 と
と の違いは、温度を表す場合の基準の違いでしかなく、目盛りには全く違いが無い。
の違いは、温度を表す場合の基準の違いでしかなく、目盛りには全く違いが無い。
このため、明示的に基準が示される温度差を表す場合において、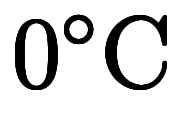 と
と は完全に等価となる。
は完全に等価となる。
例えば、状態 と状態
と状態 があり、それぞれの温度や
があり、それぞれの温度や を基準とする温度差は、
を基準とする温度差は、
セルシウス温度と絶対温度ではそれぞれ次のように表現できる:
| 座標系 | 対象温度 | 基準温度 | 温度差 |
|---|---|---|---|
| セルシウス温度 |  | 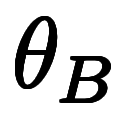 |     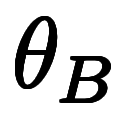 |
| 絶対温度 |  | 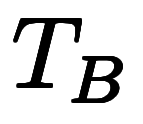 |     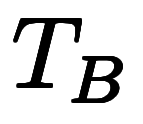 |
温度も温度差も座標系に依存しないため、

 、
、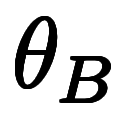

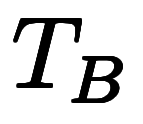 、
、

 である。
である。
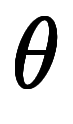



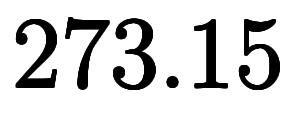
 を代入しても、下駄の部分が打消して、辻褄は合う。
を代入しても、下駄の部分が打消して、辻褄は合う。
|





