![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
温度単位の変換 のバックアップ(No.27) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
温度単位の変換 のバックアップ(No.27) |
温度単位の換算 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
温度の場合は

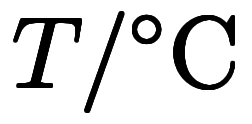 、
、

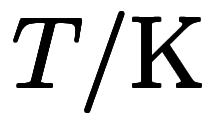 と表記でき*4、温度単位の換算はこうなる:
と表記でき*4、温度単位の換算はこうなる:
|
 、セルシウス温度を
、セルシウス温度を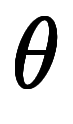 と書き分けるている。
と書き分けるている。 に統一する。
に統一する。


一般に、温度と比例関係にある法則を定式化した場合、量の方程式は当然比例式になる。
しかし、数値方程式では、絶対温度 を用いた場合は同形の比例式になるのに対し、
を用いた場合は同形の比例式になるのに対し、
セルシウス温度 を用いた場合は比例式にならず少し複雑な式に化ける。
を用いた場合は比例式にならず少し複雑な式に化ける。
例えば、シャルルの法則では気体の温度 は体積
は体積 に比例し*5、量方程式は比例式になる。
に比例し*5、量方程式は比例式になる。


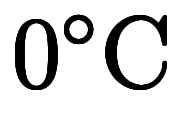 における気体の体積を
における気体の体積を とすると、シャルルの法則は表1にある各式に書けて、
とすると、シャルルの法則は表1にある各式に書けて、
セルシウス温度を用いる場合のみ、温度の項毎に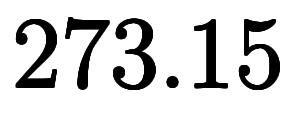 が加わり、比例式で無くなる。
が加わり、比例式で無くなる。
| 表1:シャルルの法則 | ||
|---|---|---|
| 量方程式 |   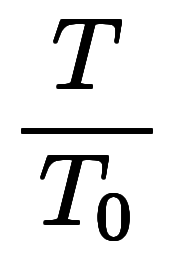 | |
| 数値 方程式 | 絶対 温度 | 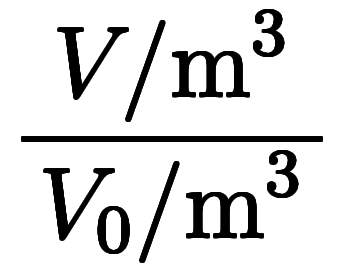  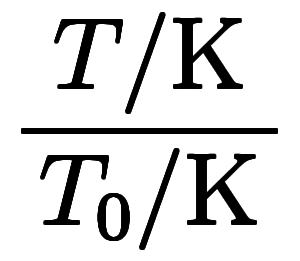 |
| セルシウス 温度 | 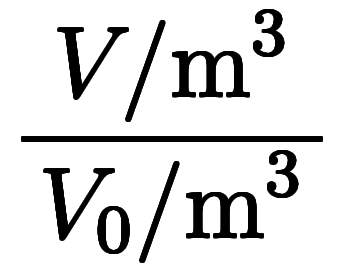  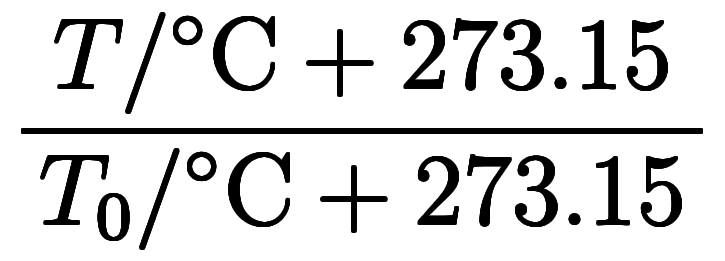  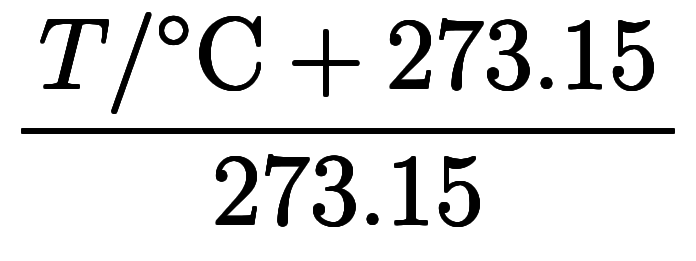 *6 *6 | |



SI単位系では と
と の違いを単位の違いと見なすが、これらを量の違いと見なすことも可能:
の違いを単位の違いと見なすが、これらを量の違いと見なすことも可能:
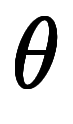 は、水の凝固点温度
は、水の凝固点温度

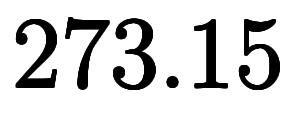
 を基準とした相対温度
を基準とした相対温度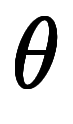 と見なす。
と見なす。 も熱力学限界値
も熱力学限界値


 を基準とした相対温度
を基準とした相対温度 と見なす。
と見なす。この視点では、 と
と の単位変換は
の単位変換は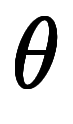 と
と の量の変換に変わる:
の量の変換に変わる:
|
相対温度において、 と
と は全く同じ単位となる。
は全く同じ単位となる。
習慣的に日常的な話をする場合に が好まれる程度の違いでしかない。
が好まれる程度の違いでしかない。
このため、 は
は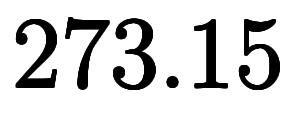
 と表記しても
と表記しても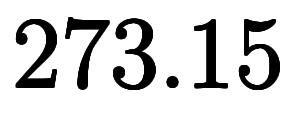
 と表記しても同じである*7。
と表記しても同じである*7。
量の換算に基づく考え方では、以下の2点において単位換算よりも汎用的と言える。



圧力では、ゲージ圧と絶対圧と呼ばれる2つの基準が良く用いられる*8。
ゲージ圧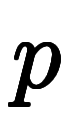 と絶対圧
と絶対圧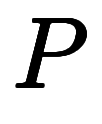 には、大気圧
には、大気圧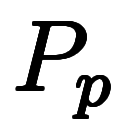 を介した加算換算が成り立つ。
を介した加算換算が成り立つ。
|
温度と事情が異なるのは、大気圧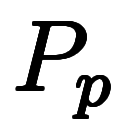 の値は、約
の値は、約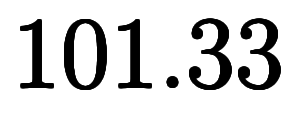
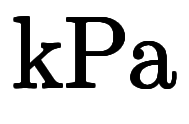 であるが、厳密には気圧変動に依存する。
であるが、厳密には気圧変動に依存する。
気圧変動は場所と時間に依存するため、ゲージ圧と絶対圧の変換を単位間の変換としては扱えない。
その結果、ゲージ圧や絶対圧は常に量の概念であり、同じ圧力単位が使われる。
ただし、工学的には単位の後ろに以下の記号を付けて明記する場合があり、
特に と
と の表記は
の表記は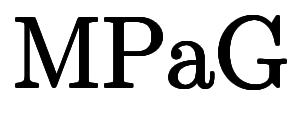 や
や と単位に空白無しで綴られ、単位のように振舞う場合がある。
と単位に空白無しで綴られ、単位のように振舞う場合がある。
|



高度では、基準点の違いで地上高度と海抜高度の2種類が良く用いられる*9:
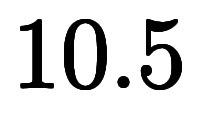
 」のように表記される。
」のように表記される。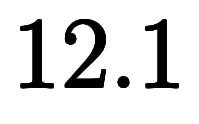
 」のように表記される。
」のように表記される。地上高度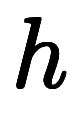 と海抜高度
と海抜高度 には、地面の海抜高度
には、地面の海抜高度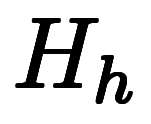 を介した加算変換が成り立つ:
を介した加算変換が成り立つ:
|
ここで、地面の海抜高度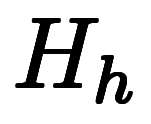 も大気圧
も大気圧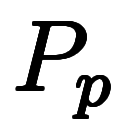 と同様、場所と時間*10に依存する。
と同様、場所と時間*10に依存する。
このため、地上高度と海抜高度を単位変換としては扱えない。
また、工学でも単位で区別する習慣は無い。



これまでに、2種類の温度換算は共に加算換算で、換算式は、
ケルビン とセルシウス度
とセルシウス度 の単位変換として考える場合は
の単位変換として考える場合は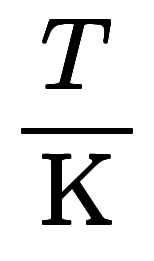

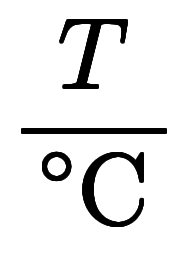

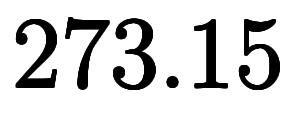 、
、
絶対温度 とセルシウス温度
とセルシウス温度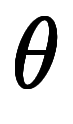 の量の変換として考える場合は
の量の変換として考える場合は

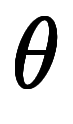

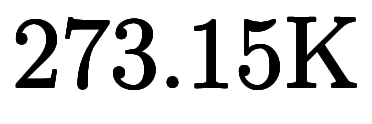 になる。
になる。
温度換算では乗算関係ではない意味で異例であるように、
シャルルの法則がケルビンでないと比例しないなど、演算に関して注意が必要な場合が多い。
量の換算で考える場合も、全てが相対温度に統一されるものの、演算の変換依存性に注意する必要がある。



例えば、状態 と状態
と状態 があり、それぞれの温度や
があり、それぞれの温度や を基準とする温度差は、
を基準とする温度差は、
セルシウス温度と絶対温度ではそれぞれ次のように表現できる:
| 座標系 | 対象温度 | 基準温度 | 温度差 |
|---|---|---|---|
| セルシウス温度 |  | 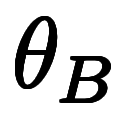 |     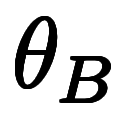 |
| 絶対温度 |  | 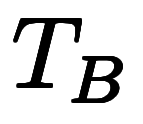 |     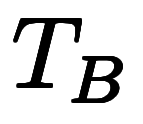 |
温度も温度差も座標系に依存しないため、

 、
、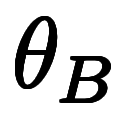

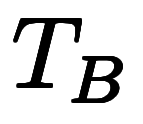 、
、

 である。
である。
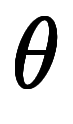



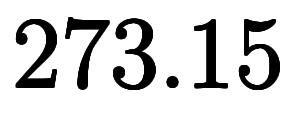
 を代入しても、下駄の部分が打消して、辻褄は合う。
を代入しても、下駄の部分が打消して、辻褄は合う。
|



状態 と状態
と状態 があり、それぞれの温度と温度比は、
があり、それぞれの温度と温度比は、
セルシウス温度と絶対温度ではそれぞれ次のように書く場合を考える:
| 座標系 | 対象温度 | 基準温度 | 温度比*11 |
|---|---|---|---|
| セルシウス温度 |  | 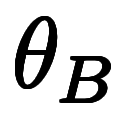 |   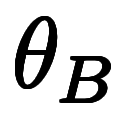 |
| 絶対温度 |  | 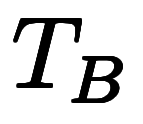 |   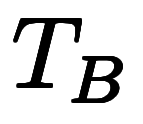 |
温度は座標系に依存しないため、

 、
、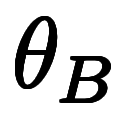

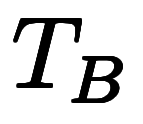 である。
である。
温度差と異なるのは、温度商は座標依存量で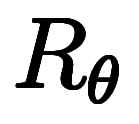
![\iro[ak]{\neq} $$ \iro[ak]{\neq} $$](./eq/eq-ni-88bca4eea86891615031bd7f5f22a339.png)
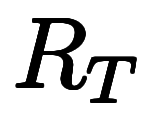 になる。
になる。
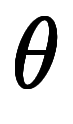



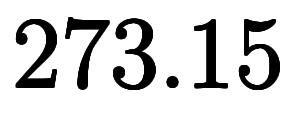
 を代入しても、下駄が打消せないのが直ちに分かる。
を代入しても、下駄が打消せないのが直ちに分かる。
|
シャルルの法則で体積商が比例するのは絶対零度を基準とした温度商に限られるため、
絶対温度に座標変換してから数値除算する必要がある。
セルシウス温度の数値除算も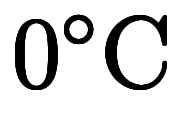 を基準にする比較では意味を持ちうるが、一般性に欠ける。
を基準にする比較では意味を持ちうるが、一般性に欠ける。
高度でも同じ関係である。
同じ2点の高度商でも、地上高度と海抜高度では単純に数値除算しても商は異なる。
しかも、建物を比べる場合は地上高度、山を比べる場合は海抜高度が用いられるように、両方が実用的意味を持つ。



|
| 座標系 | 対象温度 | 基準温度 | 温度和 |
|---|---|---|---|
| 地上高度 |  | 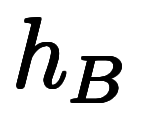 | 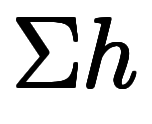    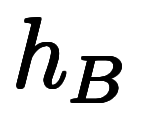 |
| 海抜高度 |  | 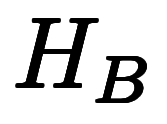 | 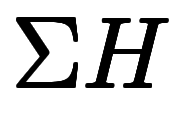    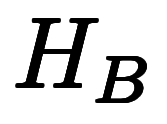 |
地上高度の和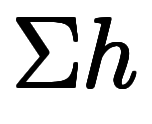 に
に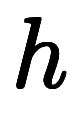



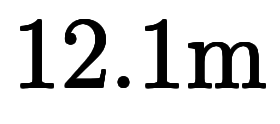 を代入すると、海抜高度の和とは異なる量になる。
を代入すると、海抜高度の和とは異なる量になる。
|
このため、高度の和は使う座標系に依存し、地上高度の和と海抜高度の和は異なる物理量になると言える。
| 地上高度 |  | 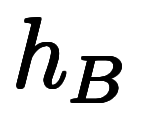 | 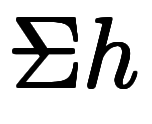    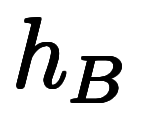 |
|---|---|---|---|
| 海抜高度 |  | 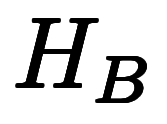 | 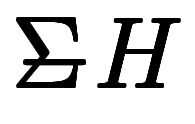    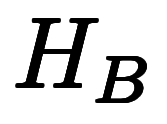 |


