![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
関数 のバックアップ(No.4) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
関数 のバックアップ(No.4) |
凌宮表記術: |
|
|
|






関数は入力と出力の関係であり、束縛変数の表記違いは関数の違いにはならない。
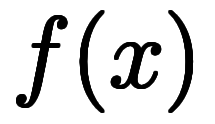

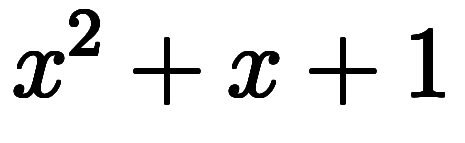 でも
でも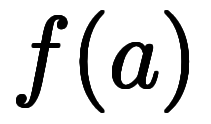

 でも、
でも、
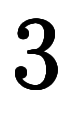 を代入したら同じ
を代入したら同じ になることに代わらない。
になることに代わらない。
 以外にも任意の数に対して同じ結果になる。
以外にも任意の数に対して同じ結果になる。
同じ代入に対して、常に同じ値になる関数は、同じ関数と見なされる。
この性質を束縛表記で以下のように明記できる。
|
|
任意の関数について、束縛変数を任意の文字に差し替えできる。



定数関数は代入した値に関係なく、定数を取る関数である。
束縛表記では、定数 に対し、定数関数は
に対し、定数関数は と表記できるが、
と表記できるが、
この束縛は形式的なもので、実際に束縛される対象となる が式
が式 に含まれて無い。
に含まれて無い。
このため、定数関数に限り、束縛の有無は区別しない。

 。
。
例えば、
とできる。



束縛子で束縛されてない変数を自由変数と呼び、束縛変数と区別する。
自由変数を含むが、束縛変数を含まないし式を変数式と呼び、関数とも区別する。
例えば、変数 を含む変数式
を含む変数式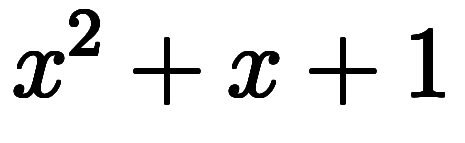 は関数
は関数 とは区別する
とは区別する
|
変数式の自由変数は、関数の束縛変数とは異なって差し替えが効かない。
変数

 であれば、
であれば、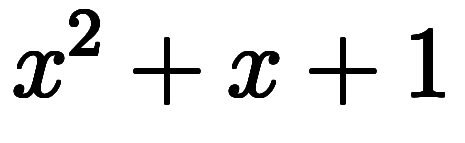

 である。
である。
|






例示2、一般的にf(x)=2x と書く場合、f:R:x=(2x):R:x=2x:R:x と厳密に表記できる。f:x=2x:x と略すが、f:p=2p:p と書いてもf:x=2p:p と書いても同じである。
2x だけなら x を不定元とする多項式に見えるが、2x:x で x を変数とする関数と書き分けできると理解して良い。
厳密表記では、定数関数と定数を区別する。
例示3値が2の定数: 2値が2の定数関数: 2:x=2:p