![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
逆格子ベクトル のバックアップの現在との差分(No.7) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
逆格子ベクトル のバックアップの現在との差分(No.7) |
格子ベクトルと逆格子ベクトル |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
一般に、基本逆格子ベクトル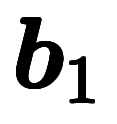 、
、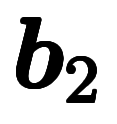 、
、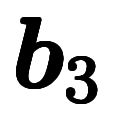 は、計算法として以下のように定義される
は、計算法として以下のように定義される
|
|
|
格子ベクトルと同様に、任意の整数を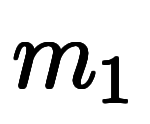 、
、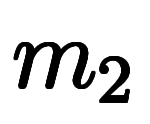 、
、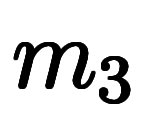 を用いて、線形結合をもって逆格子ベクトルを定義できる。
を用いて、線形結合をもって逆格子ベクトルを定義できる。
|



基本逆格子ベクトルの定義から、
基本逆格子ベクトルは対応する基本格子ベクトルの逆基底を 倍したベクトルであると言える。
倍したベクトルであると言える。
このため、凌宮数学の逆基底表記を用いると、基本逆格子ベクトルを次のように表記できる:
|
|
|
基本格子ベクトルや基本逆格子ベクトルは空間的周期性を記述するための物理量であり、
空間的に周期性を記述する物理量と比較すると理解し易い:
| 時間的周期性 | 空間的周期性 | |||||||
|---|---|---|---|---|---|---|---|---|
| 周期 |  | 波長 |  | 基本格子ベクトル |  |
| 周波数 |  |  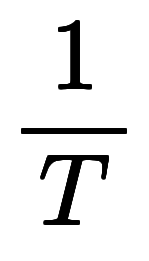 | 波数 |  |  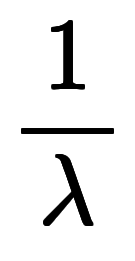 | 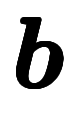 |  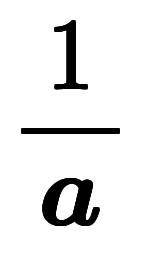 |
| 角周波数 |  |  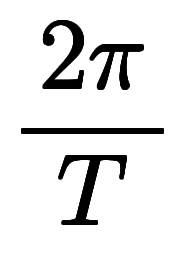 | 角波数 |  |   | 基本逆格子ベクトル | 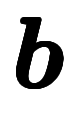 |  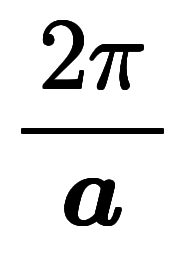 |
| 時間的周期性 | 空間的周期性 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 周期 |  | 波長 |  | 基本格子ベクトル |  |
| 周波数、振動数 |   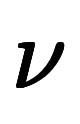 |   | 波数 | 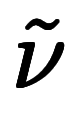     |   | 基本逆格子ベクトル | 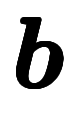 |   | |
| 角周波数、角速度 |  |  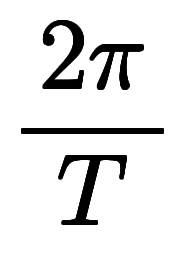 | 波数、角波数 |  |   | 基本逆格子ベクトル | 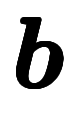 |  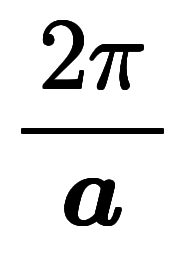 | |
 は、分野によって角波数として定義される場合があり、定義を都度確認する必要がある。
は、分野によって角波数として定義される場合があり、定義を都度確認する必要がある。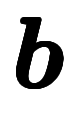 も流派によっては
も流派によっては を含めない場合があり、定義に要注意。
を含めない場合があり、定義に要注意。



 または
または になる。
になる。![\iro[ao]{\:a_1} $$ \iro[ao]{\:a_1} $$](./eq/eq-ni-df20a1f264e9c92c9687d6e6fc90a6b3.png) ![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png) ![\iro[ao]{\:b_1} $$ \iro[ao]{\:b_1} $$](./eq/eq-ni-8476d99802a7fb2a49f335a51eb2b22c.png) ![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png) ![\iro[ao]{\:a_1} $$ \iro[ao]{\:a_1} $$](./eq/eq-ni-df20a1f264e9c92c9687d6e6fc90a6b3.png) ![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png) ![\iro[ao]{\ffd{2\pi}{\:a_1}} $$ \iro[ao]{\ffd{2\pi}{\:a_1}} $$](./eq/eq-ni-b6304cecca79e28519769bf19f0e592d.png) ![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png) ![\iro[ao]{2\pi} $$ \iro[ao]{2\pi} $$](./eq/eq-ni-dec7b65f21f29a8f1c2d78daefd2a2b0.png) | ![\iro[ak]{\:a_1} $$ \iro[ak]{\:a_1} $$](./eq/eq-ni-0def88ed8aeae30d78dee5e09328c010.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\:b_2} $$ \iro[ak]{\:b_2} $$](./eq/eq-ni-987d95bc77c1a8e9482e111aa2f2cc85.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{\:a_1} $$ \iro[ak]{\:a_1} $$](./eq/eq-ni-0def88ed8aeae30d78dee5e09328c010.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\ffd{2\pi}{\:a_2}} $$ \iro[ak]{\ffd{2\pi}{\:a_2}} $$](./eq/eq-ni-90b393541bc92a515ea5b14c53074100.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) | ![\iro[ak]{\:a_1} $$ \iro[ak]{\:a_1} $$](./eq/eq-ni-0def88ed8aeae30d78dee5e09328c010.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\:b_3} $$ \iro[ak]{\:b_3} $$](./eq/eq-ni-53180ed5cf786a60e0f4a7197252cc9a.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{\:a_1} $$ \iro[ak]{\:a_1} $$](./eq/eq-ni-0def88ed8aeae30d78dee5e09328c010.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\ffd{2\pi}{\:a_3}} $$ \iro[ak]{\ffd{2\pi}{\:a_3}} $$](./eq/eq-ni-66bb83c7bd24a93d64859e8599d713ed.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) |
![\iro[ak]{\:a_2} $$ \iro[ak]{\:a_2} $$](./eq/eq-ni-7572d1e8d36a65bb0f2d991fac3a0397.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\:b_1} $$ \iro[ak]{\:b_1} $$](./eq/eq-ni-7eec20e82c4162268074326910dcdda1.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{\:a_2} $$ \iro[ak]{\:a_2} $$](./eq/eq-ni-7572d1e8d36a65bb0f2d991fac3a0397.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\ffd{2\pi}{\:a_1}} $$ \iro[ak]{\ffd{2\pi}{\:a_1}} $$](./eq/eq-ni-05b59526949eb70d362fbf8c15e1ec75.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) | ![\iro[ao]{\:a_2} $$ \iro[ao]{\:a_2} $$](./eq/eq-ni-5ccedf2475903583ed1f5f4f85aa662b.png) ![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png) ![\iro[ao]{\:b_2} $$ \iro[ao]{\:b_2} $$](./eq/eq-ni-3679f0e20227807ee9eb99e8e560e7b7.png) ![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png) ![\iro[ao]{\:a_2} $$ \iro[ao]{\:a_2} $$](./eq/eq-ni-5ccedf2475903583ed1f5f4f85aa662b.png) ![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png) ![\iro[ao]{\ffd{2\pi}{\:a_2}} $$ \iro[ao]{\ffd{2\pi}{\:a_2}} $$](./eq/eq-ni-37323b8885ecb619be33978b412a2cf1.png) ![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png) ![\iro[ao]{2\pi} $$ \iro[ao]{2\pi} $$](./eq/eq-ni-dec7b65f21f29a8f1c2d78daefd2a2b0.png) | ![\iro[ak]{\:a_2} $$ \iro[ak]{\:a_2} $$](./eq/eq-ni-7572d1e8d36a65bb0f2d991fac3a0397.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\:b_3} $$ \iro[ak]{\:b_3} $$](./eq/eq-ni-53180ed5cf786a60e0f4a7197252cc9a.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{\:a_2} $$ \iro[ak]{\:a_2} $$](./eq/eq-ni-7572d1e8d36a65bb0f2d991fac3a0397.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\ffd{2\pi}{\:a_3}} $$ \iro[ak]{\ffd{2\pi}{\:a_3}} $$](./eq/eq-ni-66bb83c7bd24a93d64859e8599d713ed.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) |
![\iro[ak]{\:a_3} $$ \iro[ak]{\:a_3} $$](./eq/eq-ni-db07c7672014e14440e1c0ef7444a90f.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\:b_1} $$ \iro[ak]{\:b_1} $$](./eq/eq-ni-7eec20e82c4162268074326910dcdda1.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{\:a_3} $$ \iro[ak]{\:a_3} $$](./eq/eq-ni-db07c7672014e14440e1c0ef7444a90f.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\ffd{2\pi}{\:a_1}} $$ \iro[ak]{\ffd{2\pi}{\:a_1}} $$](./eq/eq-ni-05b59526949eb70d362fbf8c15e1ec75.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) | ![\iro[ak]{\:a_3} $$ \iro[ak]{\:a_3} $$](./eq/eq-ni-db07c7672014e14440e1c0ef7444a90f.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\:b_2} $$ \iro[ak]{\:b_2} $$](./eq/eq-ni-987d95bc77c1a8e9482e111aa2f2cc85.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{\:a_3} $$ \iro[ak]{\:a_3} $$](./eq/eq-ni-db07c7672014e14440e1c0ef7444a90f.png) ![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png) ![\iro[ak]{\ffd{2\pi}{\:a_2}} $$ \iro[ak]{\ffd{2\pi}{\:a_2}} $$](./eq/eq-ni-90b393541bc92a515ea5b14c53074100.png) ![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png) ![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) | ![\iro[ao]{\:a_3} $$ \iro[ao]{\:a_3} $$](./eq/eq-ni-81c4646002735b5535b424a96913cea7.png) ![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png) ![\iro[ao]{\:b_3} $$ \iro[ao]{\:b_3} $$](./eq/eq-ni-b09eac088326015c3786c7cd24e41842.png) ![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png) ![\iro[ao]{\:a_3} $$ \iro[ao]{\:a_3} $$](./eq/eq-ni-81c4646002735b5535b424a96913cea7.png) ![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png) ![\iro[ao]{\ffd{2\pi}{\:a_3}} $$ \iro[ao]{\ffd{2\pi}{\:a_3}} $$](./eq/eq-ni-5ce4ee1a85926a60dddce6d5ce23b655.png) ![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png) ![\iro[ao]{2\pi} $$ \iro[ao]{2\pi} $$](./eq/eq-ni-dec7b65f21f29a8f1c2d78daefd2a2b0.png) |
 と
と 内積は必ず整数の
内積は必ず整数の 倍になる。
倍になる。      ただし、 ただし、  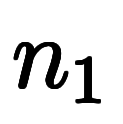 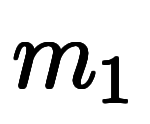  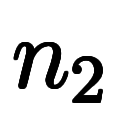 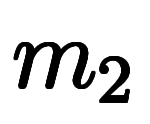  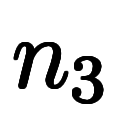 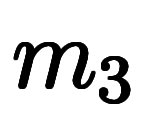 で必ず整数になる で必ず整数になる |



 など、
など、 以外の正規化条件で定義された双対基底にも応用できる。
以外の正規化条件で定義された双対基底にも応用できる。





