![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
逆基底 |
凌宮表記術:基底 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ⇔ |
|
問題になるのは、両方の基底は添字の位置で関連づけるられているため、基底の書き方が限られることである。
例えば、 、
、 、
、 が基底になる外積代数では、
が基底になる外積代数では、 、
、 、
、 をそのまま使うと不都合が生じる。
をそのまま使うと不都合が生じる。
これに対し、凌宮数学では以下のように双対基底を表記する。
| 幾何基底 | 微小基底 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 正基底 | 逆基底 | 正基底 | 逆基底 | ||||||||||
| 通常表記 |  |  | 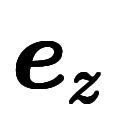 | 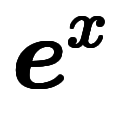 |  | 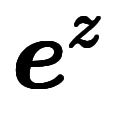 |  |  |  | ─ | ─ | ─ | |
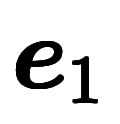 | 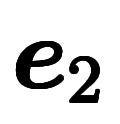 | 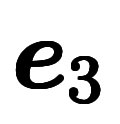 | 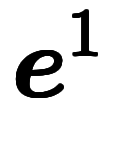 | 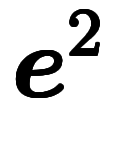 | 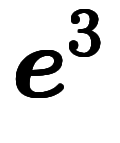 | 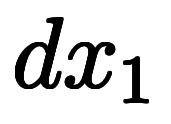 | 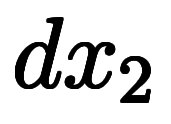 | 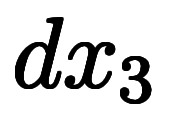 | 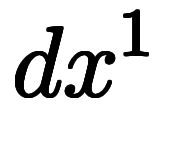 | 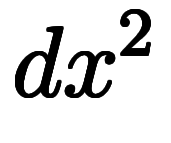 | 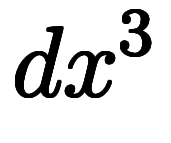 | ||
| 凌宮表記 | 分数表記 |  |  | 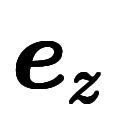 |  | 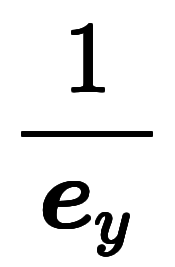 | 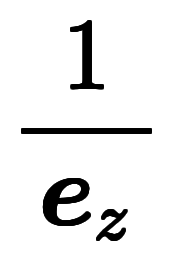 |  |  |  | 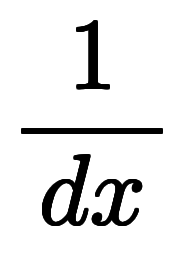 | 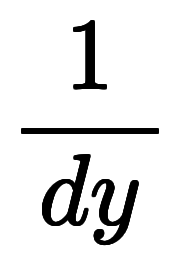 |  |
| 指数表記 | ![\iro[gy]{\:e_x^{+1}} $$ \iro[gy]{\:e_x^{+1}} $$](./eq/eq-ni-2470ae70e268d1917b06818e5f1d7e39.png) | ![\iro[gy]{\:e_y^{+1}} $$ \iro[gy]{\:e_y^{+1}} $$](./eq/eq-ni-0242816e3c10aeadf9f92c22399317e2.png) | ![\iro[gy]{\:e_z^{+1}} $$ \iro[gy]{\:e_z^{+1}} $$](./eq/eq-ni-14074a5e4352bdbf5393dd7c64997795.png) | 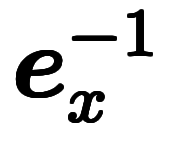 | 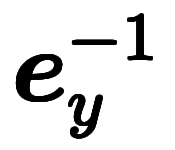 | 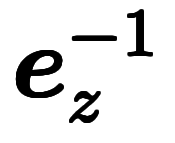 | ![\iro[gy]{dx^{+1}} $$ \iro[gy]{dx^{+1}} $$](./eq/eq-ni-0166e21e4b5e9ede12ff5bae0de7e2fe.png) | ![\iro[gy]{dy^{+1}} $$ \iro[gy]{dy^{+1}} $$](./eq/eq-ni-4bca00e9d2e2b78e64fb202bdf134f9c.png) | ![\iro[gy]{dz^{+1}} $$ \iro[gy]{dz^{+1}} $$](./eq/eq-ni-46c748f365f7f0e9756c67fd7f0df260.png) | 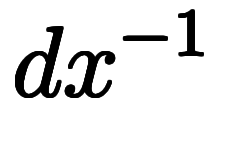 |  | 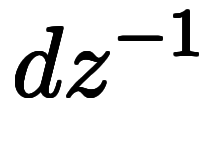 | |
| 指数略記 | ![\iro[gy]{\:e_x^+} $$ \iro[gy]{\:e_x^+} $$](./eq/eq-ni-0f48efee581ea51d88d64a0c68dee86c.png) | ![\iro[gy]{\:e_y^+} $$ \iro[gy]{\:e_y^+} $$](./eq/eq-ni-1ea463e72d76d6ae7a4728fc67d22e6b.png) | ![\iro[gy]{\:e_z^+} $$ \iro[gy]{\:e_z^+} $$](./eq/eq-ni-501eb03bd579cc09e91d062e70672c36.png) | 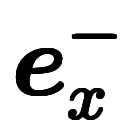 | 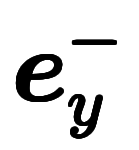 | 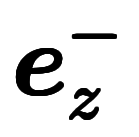 | ![\iro[gy]{dx^+} $$ \iro[gy]{dx^+} $$](./eq/eq-ni-41d720142d01b1150d7498551cf83c02.png) | ![\iro[gy]{dy^+} $$ \iro[gy]{dy^+} $$](./eq/eq-ni-0ca6e81d6b4bd60464dfa6ad31c8f318.png) | ![\iro[gy]{dz^+} $$ \iro[gy]{dz^+} $$](./eq/eq-ni-a7f85e4802e8e1dcaad175ff35e27da2.png) | 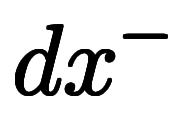 |  | 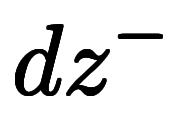 | |
逆数表記を用いたのは、逆基底が逆数と同じ発想であるため。
指数表記は、単にスカラの逆数が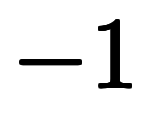 乗に書けるのに合わせているだけ。
乗に書けるのに合わせているだけ。
指数略記は、式ではなく、一塊の記号として扱いたい場合の表記である。
この他、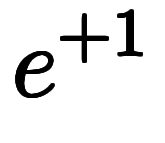 と
と は
は と
と の対称性を考慮した表記で、正基底と見なす意思の強調に使える。
の対称性を考慮した表記で、正基底と見なす意思の強調に使える。



3次元の場合、双対基底の定義を通常表記で書くと、こうなる:
|
|
|
|
|
|
|
|
|
これを凌宮表記で書くと:
|
|
|
|
|
|
|
|
|
この内、![\iro[ao]{\:e_x} $$ \iro[ao]{\:e_x} $$](./eq/eq-ni-6dba04f82d5d452615d5201f6eff594a.png)
![\iro[ao]{\sx} $$ \iro[ao]{\sx} $$](./eq/eq-ni-a2f0fcc2592435d67e2edeceb41f986e.png)
![\iro[ao]{\ffd{1}{\:e_x}} $$ \iro[ao]{\ffd{1}{\:e_x}} $$](./eq/eq-ni-fee3945ccd7783c0e04eeaf1551d5338.png)
![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png)
![\iro[ao]{1} $$ \iro[ao]{1} $$](./eq/eq-ni-c7f47b83aae2458f651d9e6c019e7b0d.png) など内積が
など内積が![\iro[ao]{1} $$ \iro[ao]{1} $$](./eq/eq-ni-c7f47b83aae2458f651d9e6c019e7b0d.png) になる正規条件は、小学校で習う逆数と全く同じである。
になる正規条件は、小学校で習う逆数と全く同じである。
対して、![\iro[ak]{\:e_x} $$ \iro[ak]{\:e_x} $$](./eq/eq-ni-fe43702f3382f9932c8d94563487610e.png)
![\iro[ak]{\sx} $$ \iro[ak]{\sx} $$](./eq/eq-ni-b6eb682dc1bb9341f27b48c947946bc7.png)
![\iro[ak]{\ffd{1}{\:e_y}} $$ \iro[ak]{\ffd{1}{\:e_y}} $$](./eq/eq-ni-174868c08aa204b68dcd3d46e0a62cf2.png)
![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png)
![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) など内積が
など内積が![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) になる直交条件も、スカラの逆数を拡張する追加条件と思えば良い。
になる直交条件も、スカラの逆数を拡張する追加条件と思えば良い。
図1は通常のベクトル除算。 自身と内積が
自身と内積が になるベクトルは無数に存在するため、逆ベクトルは一義に決まらない。
になるベクトルは無数に存在するため、逆ベクトルは一義に決まらない。
図2は基底のベクトル除算。 以外の基底と直交する条件が加わって、逆基底となる解が1つに絞られる。
以外の基底と直交する条件が加わって、逆基底となる解が1つに絞られる。
この「単独で考えず、複数の基底をセットで考える」のが、基底とベクトルとの違いであり、逆基底を定義可能にする鍵である。
正規条件と直交条件の両方が、逆数の拡張である凌宮表記の逆基底に込められる意味である。



任意の数 の逆数
の逆数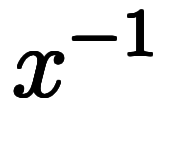 の逆数は、以下のように一種の分数計算として元の数
の逆数は、以下のように一種の分数計算として元の数 に戻る。
に戻る。
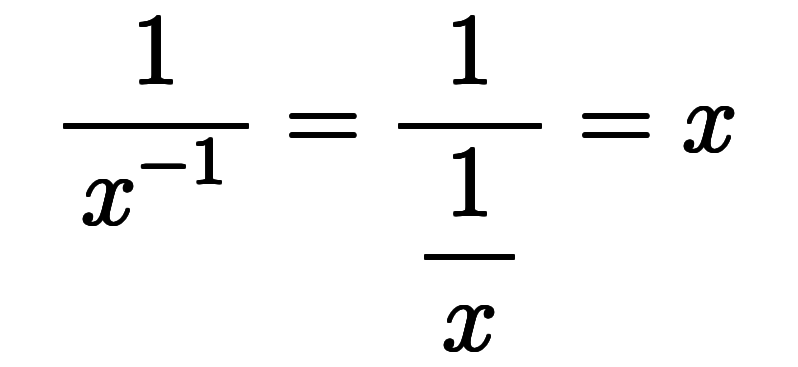 |
同様に、任意の基底 の逆基底
の逆基底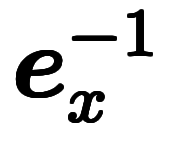 の逆基底も正基底
の逆基底も正基底 に戻る。
に戻る。
凌宮表記を用いると、逆基底の逆基底を以下のように逆数の逆数と同じように記述できる。
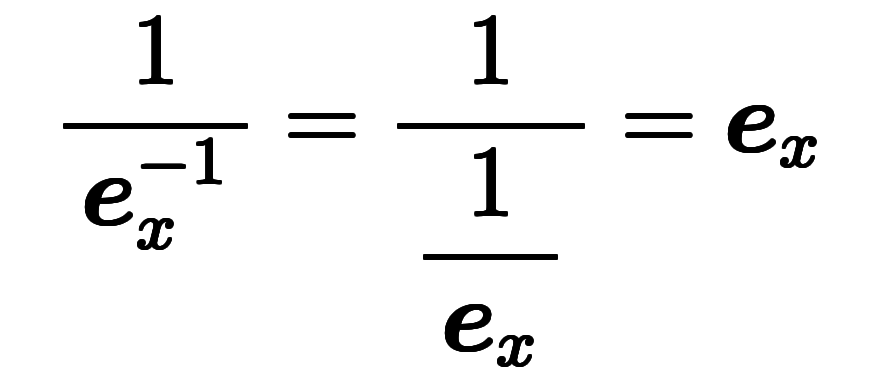 |
このように、「逆数」と「逆数を求める演算」を兼ねる逆数表記と同様、
逆数表記を流用した凌宮表記も「逆基底」と「逆基底を求める演算」の記号を両方兼ねている。
対して、通常表記は正基底と逆基底の記号を定めているに過ぎず、正基底から逆基底を求める演算の記号に成りえない。
このため、通常表記で「逆基底の逆基底」の結果である正基底を書けても、操作そのものを式で表現する手段はない。



一般に、逆基底は正基底の式で記述できる。
例えば3次元の場合は次のようになる*1:
|
これについて、凌宮表記の は、
は、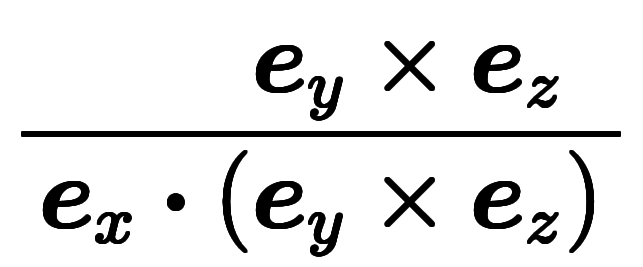 から
から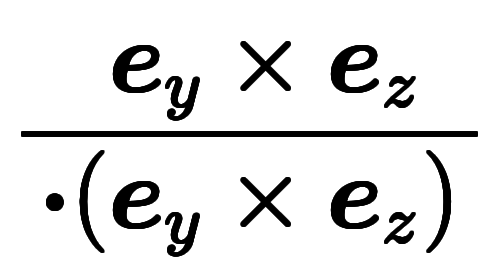 を形式的に省いたものと見なせる。
を形式的に省いたものと見なせる。
外積代数で定義される外積を用いると、より洗練された形で記述できる:
|
これなら、4次元の 座標系では次のようになるのが容易に推測できる(実際そうなる):
座標系では次のようになるのが容易に推測できる(実際そうなる):
したがって、凌宮表記の は、次元に応じた
は、次元に応じた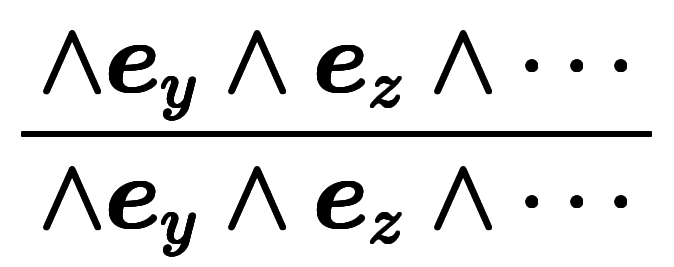 のような何かを、形式的に省いた記号と見なせる。
のような何かを、形式的に省いた記号と見なせる。
 になる; 分子はベクトル値になる; 分数線は分子の
になる; 分子はベクトル値になる; 分数線は分子の 倍という演算を表す。
倍という演算を表す。 の
の 成分
成分 


双対基底で考える場合、習慣的には以下のように成分と基底の添字を上下逆の付き方で書く*3。
|
|
|
双対基底で成分分解する場合は、ベクトルと逆基底の内積で成分を割り出せる*4*5。
例えば








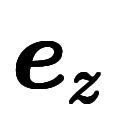 を
を と内積させると
と内積させると



 が得られる:
が得られる:
|
| |
|
| |
|
 成分と
成分と 成分も同様に求まり、これらを
成分も同様に求まり、これらを








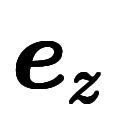 に代入すると:
に代入すると:
|
ベクトルと逆基底の内積を分数表記に纏めると、さらに簡潔な式になる:
|
1次元ではスカラ除算である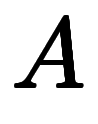

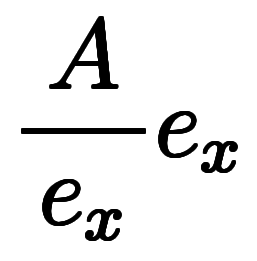 になるため、ベクトルになって成分が増える感覚のままで良い。
になるため、ベクトルになって成分が増える感覚のままで良い。
この感覚を多次元に残すことも逆基底に分数表記を用いた理由の一つである。



外積代数では、 、
、 、
、 自体を基底として扱う。
自体を基底として扱う。
凌宮表記を用いると、その逆基底は 、
、 、
、 になる。
になる。
記号的には、任意の微分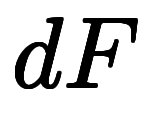 *6に対し、
*6に対し、
正基底は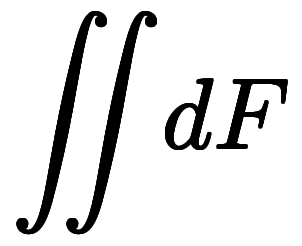



 のような積分を、逆基底は
のような積分を、逆基底は *7のような微分を作る。
*7のような微分を作る。
逆基底の定義式にある正規条件と直交条件は、
![\iro[ao]{\ddd{x}{x}} $$ \iro[ao]{\ddd{x}{x}} $$](./eq/eq-ni-377cff01caa9589cd0b76f1ae3c365a9.png)
![\iro[ao]{=} $$ \iro[ao]{=} $$](./eq/eq-ni-bb597b2673a6f4824432f1fbacb4b98c.png)
![\iro[ao]{1} $$ \iro[ao]{1} $$](./eq/eq-ni-c7f47b83aae2458f651d9e6c019e7b0d.png) や
や![\iro[ak]{\ddd{x}{y}} $$ \iro[ak]{\ddd{x}{y}} $$](./eq/eq-ni-1da4e9ecf8fa8c5419e2d0456036fff8.png)
![\iro[ak]{=} $$ \iro[ak]{=} $$](./eq/eq-ni-8d351a8c2f37e99239dda5623c86ad82.png)
![\iro[ak]{0} $$ \iro[ak]{0} $$](./eq/eq-ni-13d981a8fb9364cd5ccbe4c4166f1be8.png) のように、外積代数の基底になる条件そのものに対応する*8。
のように、外積代数の基底になる条件そのものに対応する*8。
同様に、記号的にベクトルの成分分解に適応すると全微分や1次微分形式の式が得られる:
|
ここで、 にある
にある は、ベクトル
は、ベクトル の成分分解として左辺の
の成分分解として左辺の との完全一致が要請されることに注意。
との完全一致が要請されることに注意。
さらに、 にある
にある は、微分基底
は、微分基底 そのものを表すため、やはり完全一致が要請される。
そのものを表すため、やはり完全一致が要請される。
このため、凌宮数学では偏微分でも全微分と同じ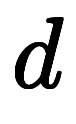 で記述する。
で記述する。
 と書くが、2次元以上では偏微分
と書くが、2次元以上では偏微分 として微分記号を変えている。これに対し、凌宮数学では一貫性のため
として微分記号を変えている。これに対し、凌宮数学では一貫性のため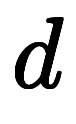 に統一している。
に統一している。

 や
や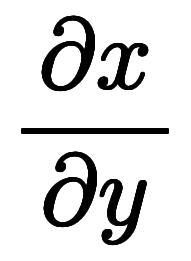

 と書く。
と書く。


凌宮数学の逆基底表記は、大学で習う双対基底を、小学校の逆数に関連付ける。
逆数と同じ記号を用いるため、(1)逆基底自身と(2)逆基底を求める演算の2通りの読み方を持つ。
形式的ではあるが、(1)と(2)に関してそれぞれ以下のように解釈できる:
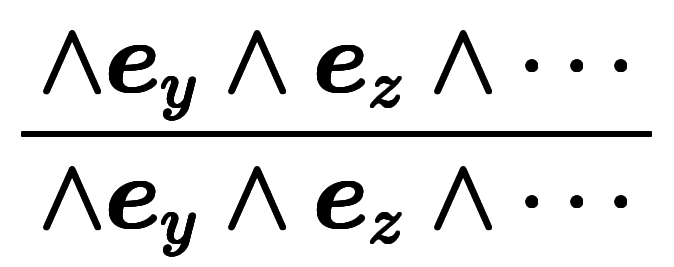 を省いた値
を省いた値



 となる
となる  を求める演算
を求める演算この表現力により、割り算、ベクトルの成分分解、全微分など、関係のある概念を統一的に記述する力を持つ。