![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
逆基底 のバックアップ(No.13) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
逆基底 のバックアップ(No.13) |
凌宮表記術:基底 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ⇔ |
|
さらに問題なのは、両方の基底は添字の位置で関連づけるられているため、基底の書き方が限られることである。
通常のベクトルでは記号の読み替えで済むが、 、
、 、
、 が基底になる外積代数では従来の表記とギャップが生じてしまう。
が基底になる外積代数では従来の表記とギャップが生じてしまう。
これに対し、凌宮数学では以下のように双対基底を表記する。
| 幾何基底 | 微小基底 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 正基底 | 逆基底 | 正基底 | 逆基底 | ||||||||||
| 通常表記 |  |  | 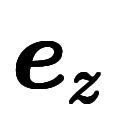 | 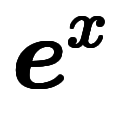 |  | 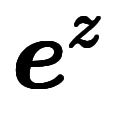 |  |  |  | ||||
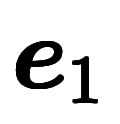 | 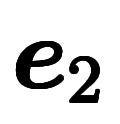 | 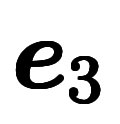 | 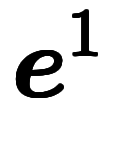 | 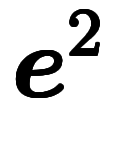 | 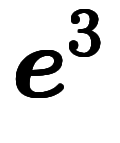 | 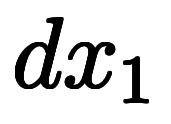 | 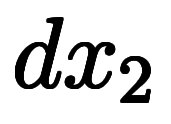 | 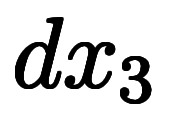 | 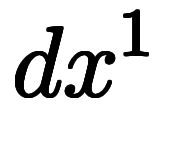 | 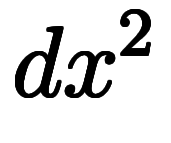 | 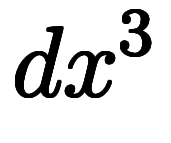 | ||
| 凌宮表記 | 分数表記 |  |  | 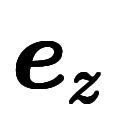 |  | 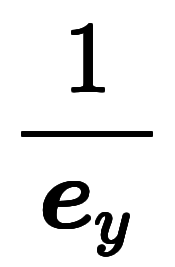 | 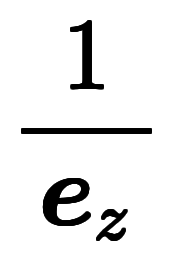 |  |  |  | 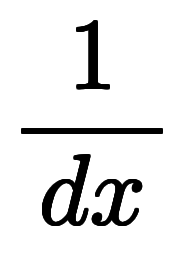 | 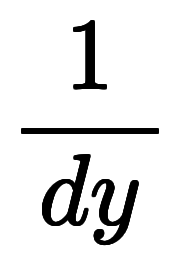 |  |
| 指数表記 | 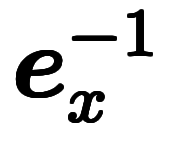 | 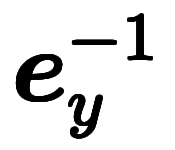 | 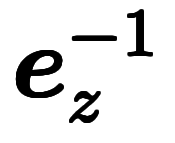 | 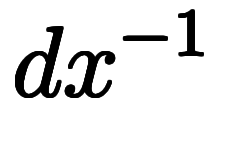 |  | 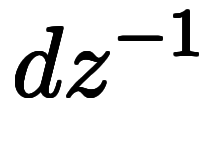 | |||||||
| 指数略記 | 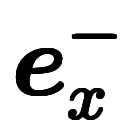 | 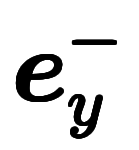 | 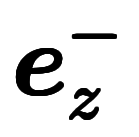 | 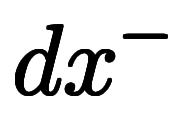 |  | 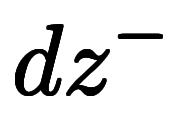 | |||||||
逆数表記を用いたのは、逆基底が逆数と同じ発想であるため。
指数表記は、単にスカラの逆数が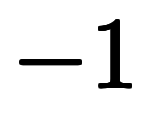 乗に書けるのに合わせているだけ。
乗に書けるのに合わせているだけ。
指数略記は、式ではなく、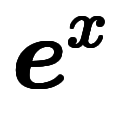 のように一塊として扱いたい場合の表記である。
のように一塊として扱いたい場合の表記である。



3次元の場合、双対基底の定義を通常表記で書くと、こうなる:
|
|
|
|
|
|
|
|
|
これを凌宮表記で書くと:
|
|
|
|
|
|
|
|
|
このうち、



 など内積が
など内積が になる正規条件は、小学校で習う逆数と全く同じである。
になる正規条件は、小学校で習う逆数と全く同じである。
同じものを同じように書くことで、小学校から培った数学センスを大学で習うベクトルに活かす手助けになる。
一方で、残る内積が になる直交条件も、スカラの逆数を拡張するための追加条件と思えば、逆数表記に含まれる。
になる直交条件も、スカラの逆数を拡張するための追加条件と思えば、逆数表記に含まれる。
図1は通常のベクトル除算である。 との内積が
との内積が になるベクトルは幾らでも存在し、逆ベクトルを一義に決められない。
になるベクトルは幾らでも存在し、逆ベクトルを一義に決められない。
図2は基底のベクトル除算である。 以外の基底と垂直という条件を追加すれば、逆基底となる解を1つに絞れる。
以外の基底と垂直という条件を追加すれば、逆基底となる解を1つに絞れる。
この「単独で考えず、複数の基底をセットで考える」のが、基底が通常のベクトルとの違いであり、逆基底を定義できる理由である。



任意の数 の逆数
の逆数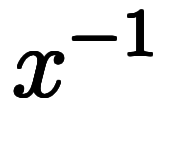 の逆数は、以下のように一種の分数計算として元の数
の逆数は、以下のように一種の分数計算として元の数 に戻る。
に戻る。
|
同様に、任意の基底 の逆基底
の逆基底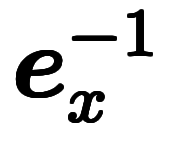 の逆基底も正基底
の逆基底も正基底 に戻る。
に戻る。
凌宮表記を用いると、逆基底の逆基底を以下のように逆数の逆数と同じように記述できる。
|
このように、「逆数」と「逆数を求める演算」を兼ねる逆数表記と同様、
逆数表記を流用した凌宮表記も「逆基底」と「逆基底を求める演算」の記号を両方兼ねている。
対して、通常表記では正基底と逆基底の記号を定めているだけで、正基底から逆基底を求める演算の記号ではない。
このため、通常表記で「逆基底の逆基底」の結果である正基底を書けても「逆基底の逆基底」自体は表現できない。
 の
の 成分
成分 


双対基底で考える場合、習慣的には以下のように成分と基底の添字を上下逆の付き方で書く*1。
|
|
|
双対基底で成分分解する場合は、ベクトルと逆基底の内積で成分を割り出せる*2。
例えば、








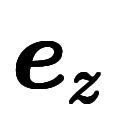 に
に との内積を取ると:
との内積を取ると:
|
|
| |
|
よって、 成分と
成分と 成分も同様に求まり、これらを
成分も同様に求まり、これらを








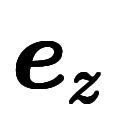 に代入すると次のようになる:
に代入すると次のようになる:
|
ベクトルと逆基底の内積を分数表記に纏めると、分かりやすい式になる。
|
1次元では、スカラ除算として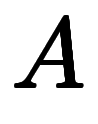

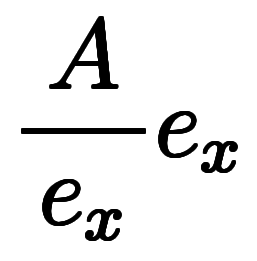 になるため、ベクトルになって成分が増える感覚のままで良い。
になるため、ベクトルになって成分が増える感覚のままで良い。
この割る感覚を多次元に残すことも逆基底に分数表記を用いた理由の一つである。



微分形式では、微分 、
、 、
、 自体をベクトルとして扱う。
自体をベクトルとして扱う。
凌宮表記を用いると、その逆基底は 、
、 、
、 と表記される。
と表記される。
記号的には、任意の微分 *3に対し、正基底は
*3に対し、正基底は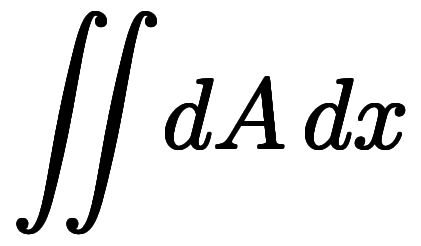 のように積分を、逆基底は
のように積分を、逆基底は のように微分*4を作る。
のように微分*4を作る。
最後に、成分分解を書くと、記号的に自ずと全微分の公式が得られる*5。
|
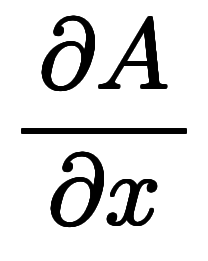 と基底とは異なる記号で表記されるが、逆基底を基底として扱えば微分記号で区別する必要が無くなる。
と基底とは異なる記号で表記されるが、逆基底を基底として扱えば微分記号で区別する必要が無くなる。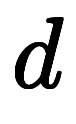 で書くことになるが、それは偏微分と常微分を区別する必要がないためである。詳しい説明は別項目で書く予定。
で書くことになるが、それは偏微分と常微分を区別する必要がないためである。詳しい説明は別項目で書く予定。


大学で習う双対基底も、逆基底を分数表記で書けば、小学校から培った割り算の感覚を利用できる。
そして、大学でベクトルとして扱われる微分の公式もベクトルの公式と同じ形になる。
逆基底も微分も一貫して分数で書けば、ベクトルも微分もずっと簡単になる。