![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
極座標系と回転座標系 のバックアップ(No.3) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
極座標系と回転座標系 のバックアップ(No.3) |
背景(暫定) |
| 点 | 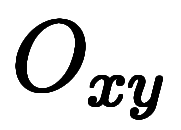 | 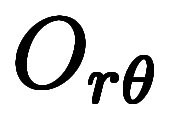 | 備考 |
 | 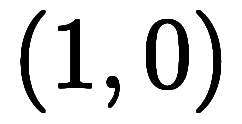 | 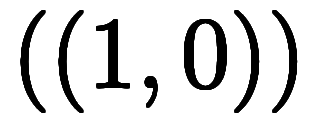 |  |
 | 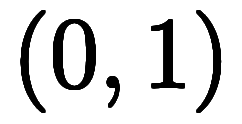 | 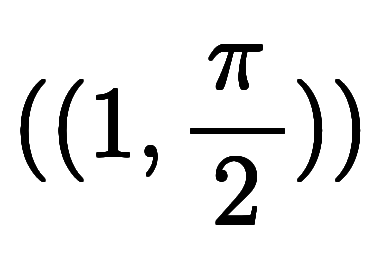 | 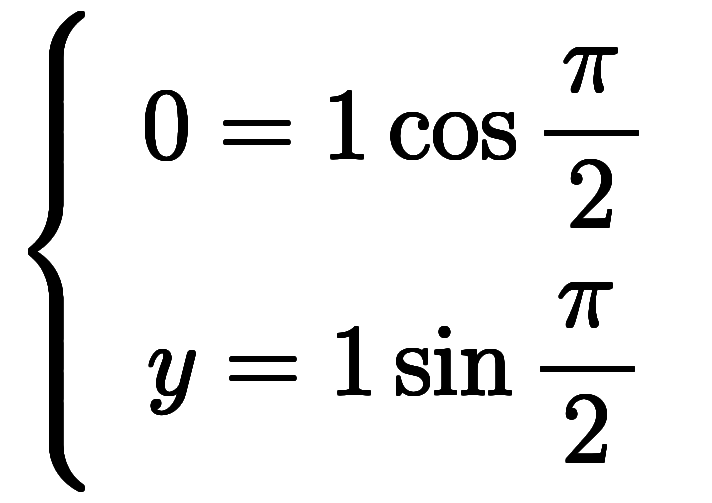 |
 | 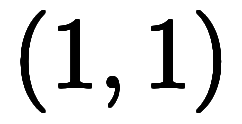 | 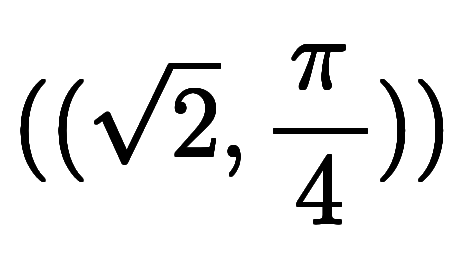 | 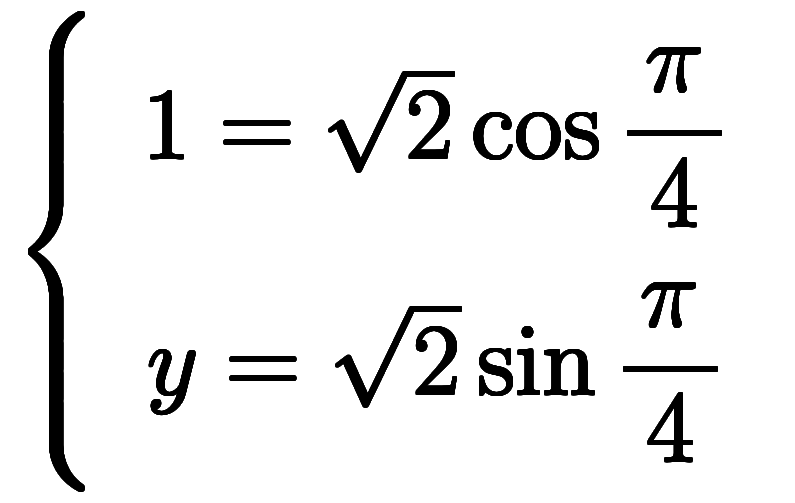 |
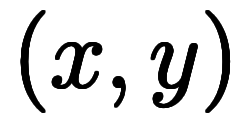 と表し、極座標を二重丸括弧で
と表し、極座標を二重丸括弧で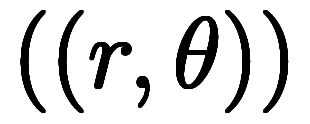 と表す。
と表す。


回転座標系とは、正規直交座標系を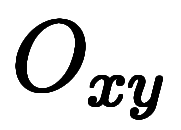 を原点回りに角度
を原点回りに角度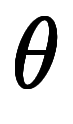 だけ回転した座標系
だけ回転した座標系 である*4。
である*4。
変換は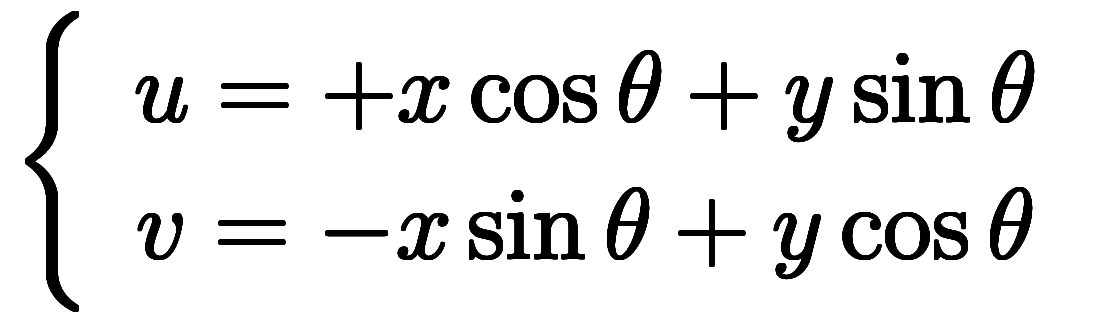 により与えられる。
により与えられる。
簡単なため、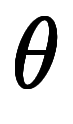

 の場合のベクトルの対応する成分を例示する。
の場合のベクトルの対応する成分を例示する。
| 点 | 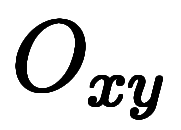 |  | 備考 |
 | 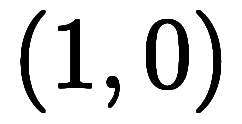 | ![[\ffd1{\sqrt2},\ffd{-1}{\sqrt2}] $$ [\ffd1{\sqrt2},\ffd{-1}{\sqrt2}] $$](./eq/eq-ni-bdf4892956f26a041d151c190697deb6.png) | 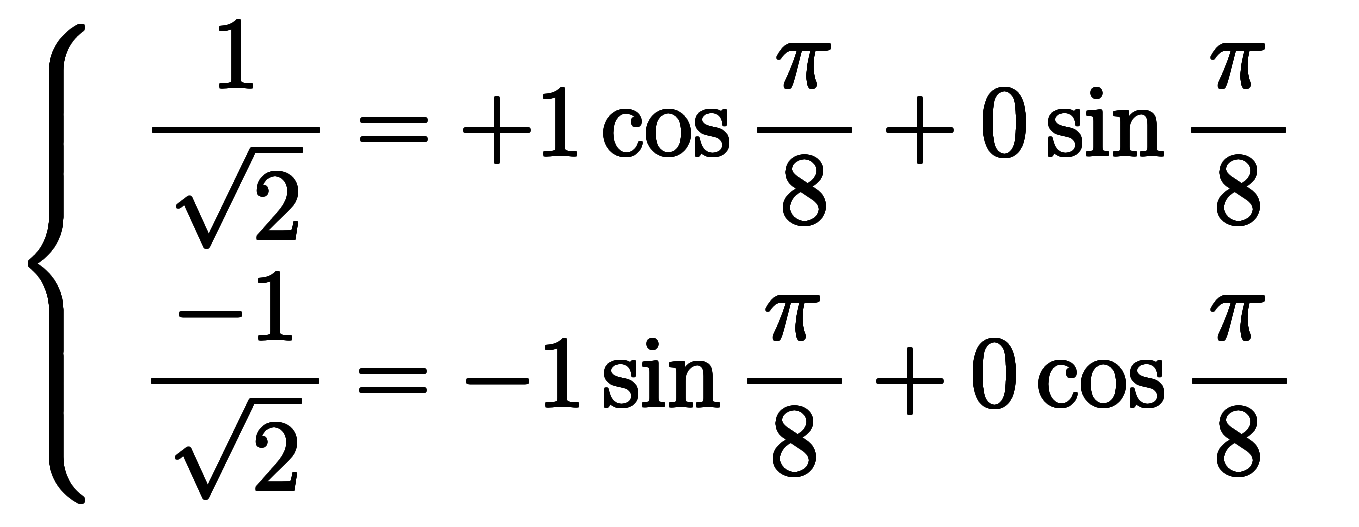 |
 | 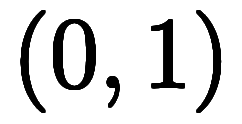 | ![[\ffd1{\sqrt2}, \ffd1{\sqrt2}] $$ [\ffd1{\sqrt2}, \ffd1{\sqrt2}] $$](./eq/eq-ni-a56eeb1af8d35f926a52d83251701f3a.png) | 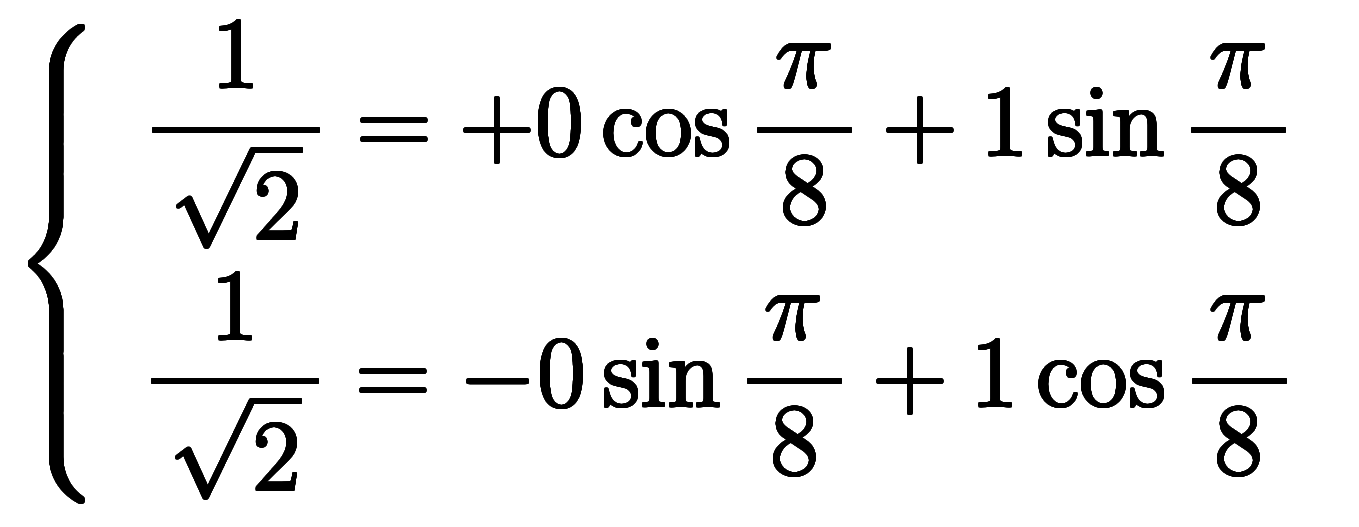 |
 |  | ![[\sqrt2 , 0] $$ [\sqrt2 , 0] $$](./eq/eq-ni-4a09e6719f17f7082ea2595a20e7a380.png) | 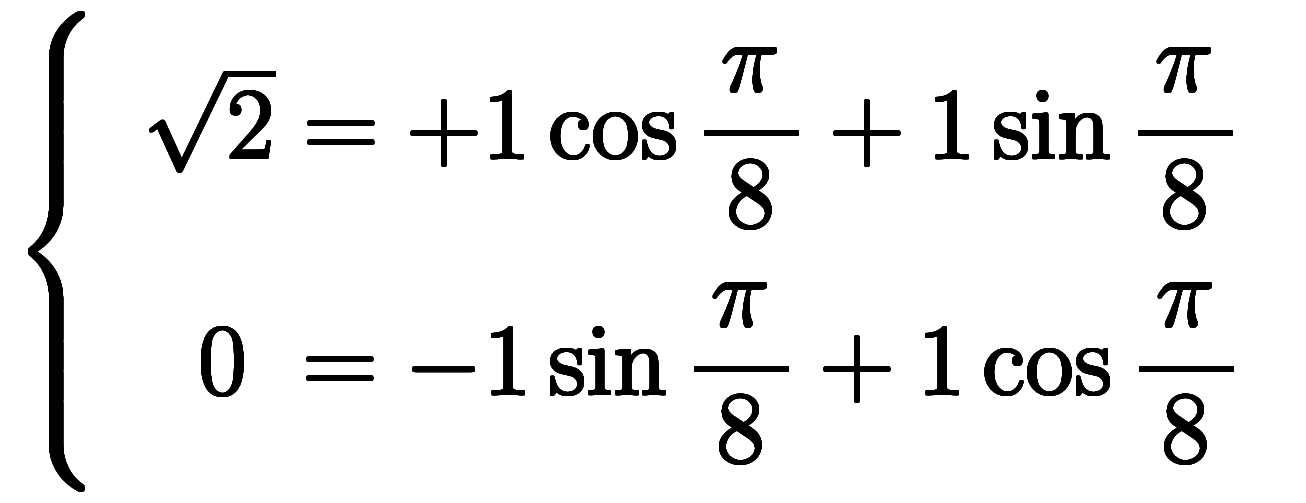 |



極座標系O_{r\theta}と回転座標系O^\theta_{uv}は既に示した通り、O_{xy}からの変換式も対応する点の座標値も異なる別の座標系である。
しかし、極座標系の基底ベクトルを導入する文脈では両方を区別せずに「極座標」と言ったりする。
例えば、http://www.th.phys.titech.ac.jp/~muto/lectures/Gmech08/chap05.pdf のP53から§5.1.2 平面極座標では、
座標値は式(5.15)が示す極座標の変換 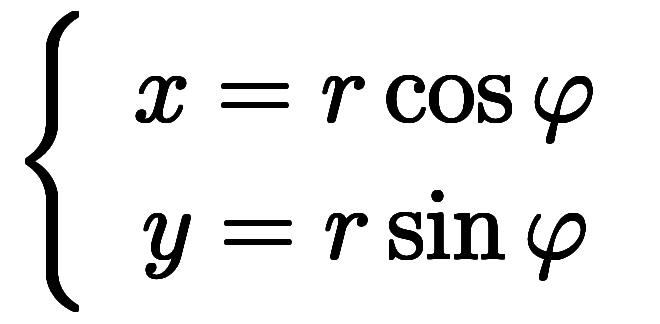 に従うのに対し、
に従うのに対し、
単位ベクトルは式(5.17)が示す回転座標系の変換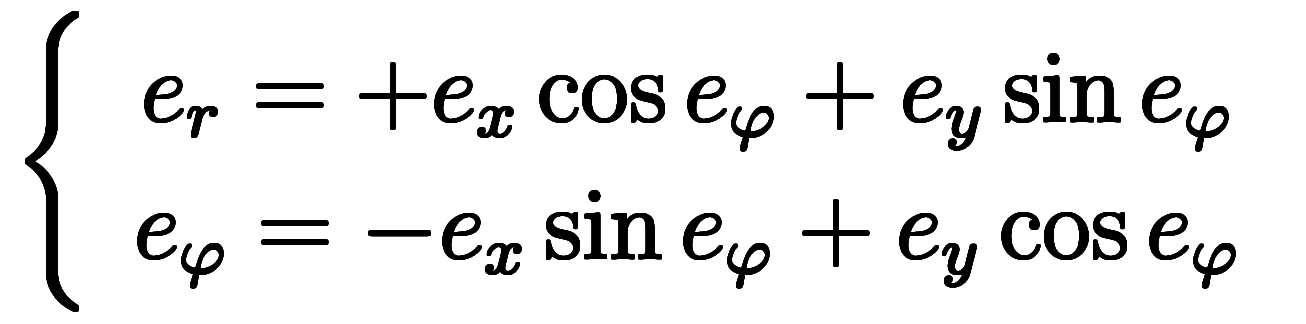 に従っている。
に従っている。
成分は具体的に書いてないが、全く同じ形をした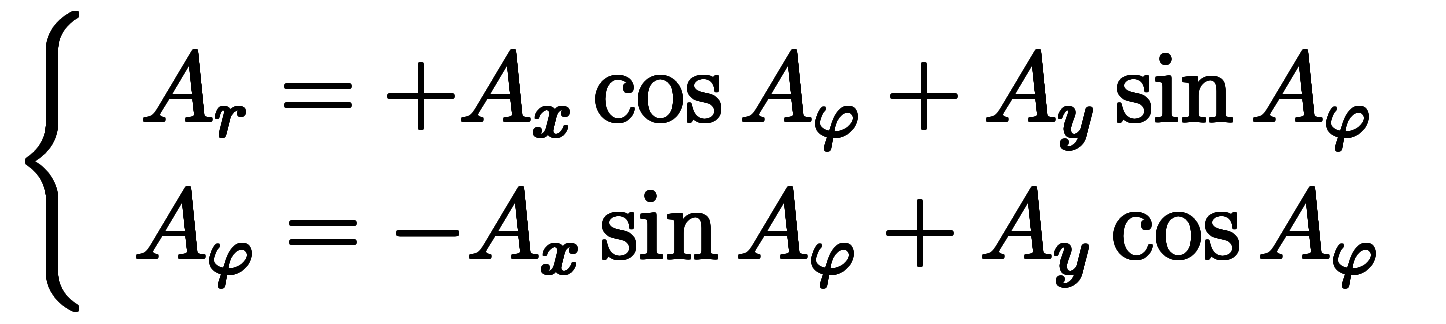 に従う。
に従う。
http://www.th.phys.titech.ac.jp/~muto/lectures/Gmech08/chap05.pdf