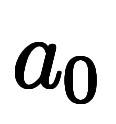![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
線形演算子で繋がる特性方程式 のバックアップ(No.6) |
![[PukiWiki] [PukiWiki]](image/NekoPunch.png)
|
線形演算子で繋がる特性方程式 のバックアップ(No.6) |
背景 |
漸化式: |
|
|
特性方程式: |
|
|
等式変形: |
|
|
ここで、数列 

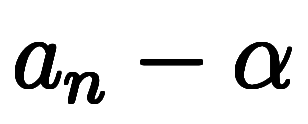 を考えば、初項
を考えば、初項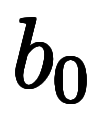

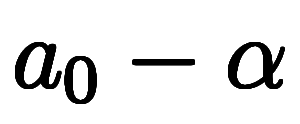 、公比
、公比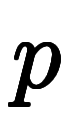 の数列のため、
の数列のため、
その一般項は、
|
 を移項すれば、
を移項すれば、 の一般項が求まる。
の一般項が求まる。
|



連続3項の漸化式として、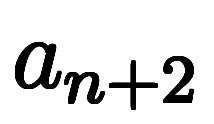

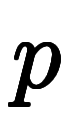
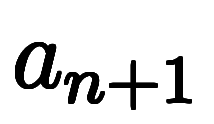

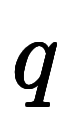


 のタイプの問題も高校で扱う。
のタイプの問題も高校で扱う。
解き方は、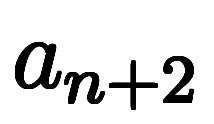 を
を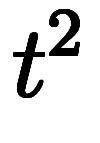 、
、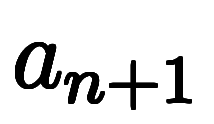 を
を 、
、 を
を に差し替えた特性方程式
に差し替えた特性方程式 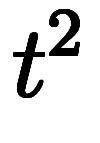

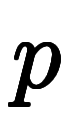


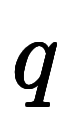

 を解き、
を解き、
その解を と
と と置けば*6、特性方程式が
と置けば*6、特性方程式が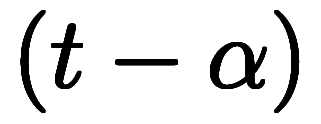
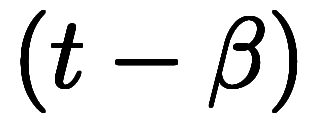

 となる。
となる。
すると、解と係数の関係で 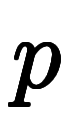




 、
、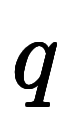


 と言えるので、これを利用して、
と言えるので、これを利用して、
漸化式を数列 と
と の式と、公比が
の式と、公比が の漸近式に分離した形に変形できる。
の漸近式に分離した形に変形できる。
|
|
|
同様に、 と
と が対称的なので、逆に扱った変換もできて、
が対称的なので、逆に扱った変換もできて、
|
それぞれから等比数列を出して、
|
|
さらに数列の差を取れば、
|
よって、
|






一般に微分可能な1変数関数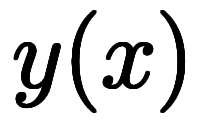 を
を を
を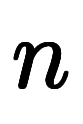 回微分した
回微分した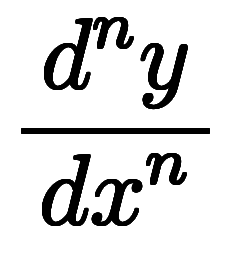 を全て
を全て の常微分と言い、
の常微分と言い、
常微分の線形結合

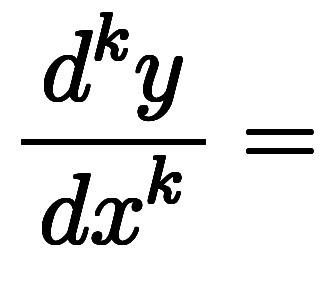
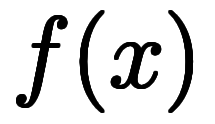 を線形常微分方程式と呼ぶ。
を線形常微分方程式と呼ぶ。
全ての が
が に対して定数である場合、定数係数線形常微分方程式と呼ぶ。
に対して定数である場合、定数係数線形常微分方程式と呼ぶ。
要は具体に、
1階定数係数線形常微分方程式は |
| |
2階定数係数線形常微分方程式は |
|
|
煩わしいので、一般的には を省き、最高階の係数を
を省き、最高階の係数を とし、微分演算子
とし、微分演算子

 を導入する。
を導入する。
1階定数係数線形常微分方程式: |
| |
2階定数係数線形常微分方程式: |
|
|



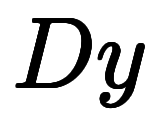

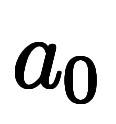


 は
は 

 と置くことで解ける。
と置くことで解ける。
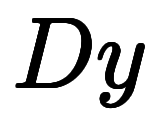




 のため、
のため、
方程式は